Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Балгабеков Т.К. 1 Оразалина А.Б. 1

---

1 Карагандинский государственный технический университет

Приведены формулы для расчетов системы, предназначенной для обслуживания и обработки каких – либо заявок, поступивших на нее в случайные моменты времени. Различая классификации СМО, был выбран наиболее подходящий вид и, имея основные показатели работы международного коридора, были произведены расчеты.

Статья в формате PDF

1179 KB

система массового обслуживания (СМО)

автомобильный транспорт

международный транспортный коридор (МТК)

одноканальные системы массового обслуживания с неограниченной очередью

1. Агеенко И.В. Лабораторный практикум по моделированию систем: учебное пособие / И.В. Агеенко, О.М. Демиденко. – гомель: учреждение образования «Гомельский государственный университет имени Франциска Скорины». – 2002.

2. Орлов Б.П. Развитие транспорта СССР. 1917–1962. – М., 1963.

3. Указ Президента Республики Казахстан от 11 апреля 2006 года № 86 Транспортная стратегия Республики Казахстан до 2015 года.

4. Балгабеков Т.К. Перспективы развитие транспортных коридоров Республики Казахстан. Современные тенденции в образовании и науке. Сборник научных трудов по материалам Научно-практической конференции, 31 октября 2013 г., часть 21, г. Тамбов, РФ.

5. Балгабеков Т.К., Адилова Н.Д., Исина Б.М., Жанатов И.М., Оразалина А.Б., Развитие Казахстанских участков дорог в международных транспортных коридорах. Международный журнал прикладных и фундаментальных исследований. – 2014.

Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания каких-либо заявок (требований), поступающих на нее в случайные моменты времени. Любое устройство, непосредственно занимающееся обслуживанием заявок, называется каналом обслуживания (или «прибором»). СМО бывают как одно-, так и многоканальными [1].

Различают СМО с отказами и СМО с очередью. В СМО с отказами заявка, пришедшая в момент, когда все каналы заняты, получает отказ, покидает СМО, а в дальнейшем в процессе ее работы не участвует. В СМО с очередью заявка, пришедшая в момент занятости всех каналов, не покидает СМО, а становится в очередь и ждет, пока не освободится какой-либо канал. Число мест в очереди т может быть как ограниченным, так и неограниченным. При т = 0 СМО с очередью превращается в СМО с отказами. Очередь может иметь ограничения не только по количеству стоящих в ней заявок (длине очереди), но и по времени ожидания (такие СМО называются «системами с нетерпеливыми клиентами»).

Аналитическое исследование СМО является наиболее простым, если все потоки событий, переводящие ее из состояния в состояние, – простейшие (стационарные пуассоновские). Это значит, что интервалы времени между событиями в потоках имеют показательное распределение с параметром, равным интенсивности соответствующего потока. Для СМО это допущение означает, что как поток заявок, так и поток обслуживания – простейшие. Под потоком обслуживания понимается поток заявок, обслуживаемых одна за другой одним непрерывно занятым каналом. Этот поток оказывается простейшим, только если время обслуживания заявки tобсл представляет собой случайную величину, имеющую показательное распределение. Параметр этого распределения μ есть величина, обратная среднему времени обслуживания: 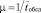, где 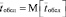. Вместо фразы «поток обслуживания – простейший» часто говорят «время обслуживания – показательное». Всякая СМО, в которой все потоки простейшие, называется простейшей СМО.

Если все потоки событий простейшие, то процесс, протекающий в СМО, представляет собой марковский случайный процесс с дискретными состояниями и непрерывным временем. При выполнении некоторых условий для этого процесса существует финальный стационарный режим, при котором как вероятности состояний, так и другие характеристики процесса не зависят от времени.

Задачи теории массового обслуживания – это нахождение вероятностей различных состояний СМО, а также установление зависимости между заданными параметрами (числом каналов п, интенсивностью потока заявок λ, распределением времени обслуживания и т.д.) и характеристиками эффективности работы СМО. В качестве таких характеристик могут рассматриваться, например, следующие:

– среднее число заявок А, обслуживаемое СМО в единицу времени, или абсолютная пропускная способность СМО;

– вероятность обслуживания поступившей заявки Q или относительная пропускная способность СМО; Q = А/λ;

– вероятность отказа Ротк, т.е. вероятность того, что поступившая заявка не будет обслужена и получит отказ; Ротк = 1 – Q;

– среднее число заявок в СМО (обслуживаемых или ожидающих в очереди) ;

– среднее число заявок в очереди ;

– среднее время пребывания заявки в СМО (в очереди или под обслуживанием) ;

– среднее время пребывания заявки в очереди ;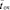

– среднее число занятых каналов .

В общем случае все эти характеристики зависят от времени. Но многие СМО работают в неизменных условиях достаточно долгое время, и поэтому для них успевает установиться режим, близкий к стационарному. Мы здесь повсюду, не оговаривая этого каждый раз специально, будем вычислять финальные вероятности состояний и финальные характеристики эффективности СМО, относящиеся к предельному стационарному режиму ее работы.

СМО называется открытой, если интенсивность поступающего на нее потока заявок не зависит от состояния самой СМО. Для любой открытой СМО в предельном стационарном режиме среднее время пребывания заявки в системе выражается через среднее число заявок в системе с помощью формулы Литтла:

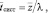(1)

где λ – интенсивность потока заявок.

Аналогичная формула (называемая также формулой Литтла) связы-вает среднее время пребывания заявки в очереди 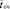и среднее число заявок в очереди:

(2)

Формулы Литтла очень полезны, так как позволяют вычислять не обе характеристики эффективности (среднее время пребывания и среднее число заявок), а только какую-нибудь одну из них.

Специально подчеркнем, что формулы (1) и (2) справедливы для любой открытой СМО (одноканальной, многоканальной, при любых видах потоков заявок и потоков обслуживания); единственное требование к потокам заявок и обслуживании – чтобы они были стационарными.

Аналогично универсальное значение для открытых СМО имеет формула, выражающая среднее число занятых каналов через абсолютную пропускную способность А:

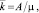
где 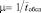– интенсивность потока обслуживания.

Очень многие задачи теории массового обслуживания, касающиеся простейших СМО, решаются при помощи схемы гибели и размножения. Финальные вероятности состояний выражаются формулами:

…;

…,

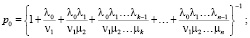
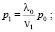
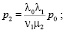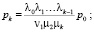
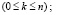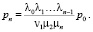
Ниже приводится без вывода ряд формул, выражающих финальные вероятности состояний и характеристики эффективности для некоторых часто встречающихся типов СМО.

Одноканальная СМО с неограниченной очередью. На одноканальную СМО поступает простейший поток заявок с интенсивностью λ. Время обслуживания – показательное с параметром 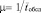. Длина очереди не ограничена. Финальные вероятности существуют только при 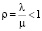(при ρ ≥ 1 очередь растет неограниченно). Состояния СМО нумеруются по числу заявок в СМО, находящихся в очереди или обслуживаемых:

S0 – СМО свободна;

S1 – канал занят, очереди нет;

S2 – канал занят, одна заявка стоит в очереди;

...;

Sk – канал занят, k–1 заявок стоят в очереди;

... .

Финальные вероятности состояний выражаются формулами:

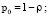
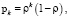
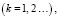
где .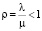

Характеристики эффективности СМО:

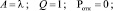
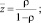
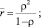
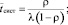
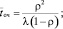
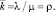
Международный транспортный коридор – высокотехнологическая транспортная система, концентрирующая на генеральных направлениях транспорт общего пользования (железнодорожный, автомобильный, морской, трубопроводный) и телекоммуникации.

МТК наиболее эффективно функционирует в условиях преференциального режима, включая единое таможенное или экономическое пространство.

Концентрация материальных, финансовых и информационных потоков в сочетании с высоким качеством экспедиторского обслуживания обеспечивают ускорение оборачиваемости капитала и синхронизации прохождения товаров и платёжных и других документов [2].

Географическое расположение Казахстана в центре Евроазиатского континента предопределяет его значительный транспортный потенциал в области транзитных перевозок.

Протяженность наземных транспортных магистралей республики составляет 106 тыс. км. Из них 13,5 тыс. км – магистральные железные дороги, 87,4 тыс. км – автомобильные магистрали общего пользования с твердым покрытием, 4 тыс. км. – речные пути [4].

Основными международными транзитными коридорами Казахстана являются:

1. Ташкент – Шымкент – Тараз – Алматы – Хоргос;

2. Шымкент – Кызылорда – Актобе – Уральск – Самара;

3. Алматы – Караганды – Астана – Петропавловск;

4. Астрахань – Атырау – Актау – граница Туркменистана;

5. Омск – Павлодар – Семипалатинск – Майкапшагай;

6. Астана – Костанай – Челябинск – Екатеринбург [5].

Международный автомобильный коридор «Алматы – Караганды – Астана – Петропавловск – гр. РФ» рассматривается как одноканальная система. В течении суток по данной автомобильной дороге проезжает 2599 автомобилей [3]. Из этого следует что, интенсивность движения на данном участке составляет 44 автомобиля в час. Среднее временное расстояние между автомобилями 1,5 минут. Определим характеристики СМО и проведем анализ работы.

1. Интенсивность нагрузки.

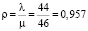
Интенсивность нагрузки ρ = 0,957 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.

Поскольку ρ < 1, то очередь не будет расти бесконечно, следовательно, предельные вероятности существуют.

2. Время обслуживания.

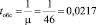час.

3. Вероятность, что канал свободен (доля времени простоя канала).

p0 = 1 – ρ = 1 – 0,957 = 0,0435

Следовательно, 4 % в течение часа канал будет не занят, время простоя равно tпр = 2,6 мин.

Вероятность того, что в очереди:

1 заявка:

p1 = ρk(1 – ρ) = 0,9571(1 – 0,957) = 0,0416

4. Доля заявок, получивших отказ (вероятность отказа).

Поскольку отказ в обслуживании в таких системах не может быть, то

pотк = 0.

Заявки не получают отказ. Обслуживаются все поступившие заявки, pотк = 0.

5. Относительная пропускная способность.

Поскольку в рассматриваемой СМО ограничение на длину очереди отсутствует, то любая заявка может быть обслужена, поэтому Q = pобс = 1.

Вероятность того, что заявка будет принята в систему: pсис = 1.

6. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок).

A = λ = 44 заявок/час.

7. Среднее число заявок в очереди (средняя длина очереди).

.

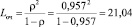8. Среднее время ожидания заявки в очереди (Среднее время простоя СМО).

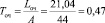час.

9. Среднее число обслуживаемых заявок.

Lоб = ρ = 0,957.

10. Среднее число заявок в системе.

LCMO = Lоч + Lобс = 21,04 + 0,957 = 22 ед.

11. Среднее время пребывания заявки в СМО (как в очереди, так и под обслуживанием).

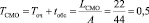час.

Число заявок, получивших отказ в течение час: λ∙p1 = 0 заявок в час.

Номинальная производительность СМО: 1/0,0217 = 46 заявок в час.

Фактическая производительность СМО: 44/46 = 96 % от номинальной производительности.

Различая классификации СМО был выбран наиболее подходящий вид и имея основные показатели работы международного коридора, были произведены расчеты. В ходе работы

Библиографическая ссылка