Все явления природы протекают во времени. Практически во всех направлениях науки, изучающей мир, время является основной метрикой. Вместе с тем «только с помощью простых опытов, допускающих наглядное представление, можно по-настоящему понять сущность времени» [1]. Для лучшего понимания сущности проходимых процессов в пространстве и времени, необходимо иметь аппарат для их совместного визуального моделирования.
На данный момент моделирование с использованием времени представляет собой процесс построения статических моделей в трехмерном пространстве, где время равно нулю (t=0). После чего происходит сложение в единую модель, т.е. происходит так называемое «покадровое» моделирование. Данное обстоятельство не позволяет моделировать одновременно и пространство и время.
Моделирование в системе «пространство-время»
Моделирование, как правило, ведется в декартовой системе координат, которая представляется взаимно-перпендикулярными осями, выходящими из одной точки. На самом деле подобное моделирование должно осуществляться в четырехмерной системе, т.е. «время должно быть отнесено к координатной системе» [2].
Время и пространство (путь) – основные составляющие вычисления скорости, а значит именно эти величины и должны влиять на моделирование объекта, движущегося на определенной скорости, и обратно, скорость должна влиять на пространство и время. Эти величины должны быть увязаны между собой при моделировании объектов в одной системе отсчета. Данное обстоятельство должно быть верно, как для покоящейся, так и для движущейся системы отсчета.
Как должна выглядеть проекция четырехмерной системы координат для визуального моделирования процессов в системе пространство-время? По мнению автора, она должна представлять собой связанную систему, представленную на рис. 1, где к декартовой системе добавляется ось времени, причем ось времени Ot равноудалена от всех пространственных осей Ox, Oy и Oz. Это утверждение может быть верным при скорости объекта равной нулю в покоящейся системе отсчета, которая не зависит от времени протекания процесса.
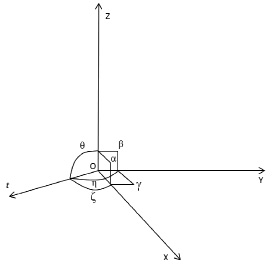
Рис. 1. Система моделирования при скорости объекта равной нулю в покоящейся системе отсчета
Обозначим углы между осями как: α=∟ZOX; β=∟ZOY; γ=∟XOY; ζ=∟tOX; η=∟tOY; θ=∟tOZ.
Углы между пространственными осями α=β=γ=90°(рис. 1), а углы между пространственной осью и осью времени ζ=η=θ ≈2,18627≈125°16’(рис. 1). Это можно вычислить, если отложить на каждой из осей равные отрезки, соединить их между собой и вписать полученную пирамиду в шар.
Согласно «Специальной теории относительности» А.Эйнштейна и следствия преобразований Лоренца, пространство изменяется относительно скорости, с которой движется объект [2, 3]. Скорость это величина, которая зависит не только от пройденного пути, но и от времени. Можно сделать вывод, что для моделирования в системе пространство-время для объектов, движущихся со скоростью больше нуля, необходимо учитывать и скорость объекта, т.к. она влияет и на его физическое состояние, одна из характеристик которого (длина) описывается по формуле (1) [2: с. 419],
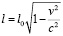 , (1)
, (1)
где l0 – длина тела в покое.
Ввиду того, что длина тела рассчитывается по формуле (1), а «кинематическая форма равномерно и прямолинейно движущегося тела зависит от его скорости относительно системы отсчета, причем кинематическая форма тела отличается от его геометрической формы» [2: с. 74], можно сделать вывод, что при увеличении скорости происходит изменение проекции объекта в пространстве по всем осям системы координат.
Для объекта, движущегося со скоростью близкой к скорости света, время замедляется, а его величина изменяется. Это позволяет предположить, что необходимо трансформировать не только сам объект в рассматриваемой системе координат (рис. 1), но и саму систему в целом путем увеличения углов α, β, γ и уменьшения углов ζ, η, θ.
На рис. 2.а показан процесс трансформации (отклонения) осей X, Y, Z, t системы при скорости объекта равной нулю (v=0) в систему моделирования с осями X’, Y’, Z’, t’ при v>0. В случае, когда собственная скорость объекта наблюдения стремится к скорости света v→c, углы α’=β’=γ’→120° (рис. 2.б), а углы ζ’=η’=θ’→90°.
В случае, когда 0<v<c, проекции точек на осях откладываются не под прямым углом, а под углом отклонения осей, как это показано на примере точки U (рис. 3).
a б
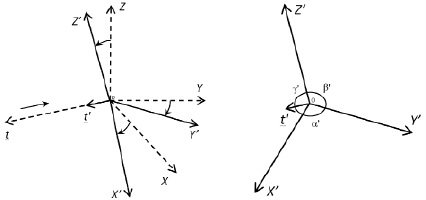
Рис. 2. Система моделирования при v→c
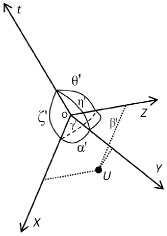
Рис. 3. Система моделирования при 0<v<c
Исходя из указанных предположений, следует рассмотреть систему отсчета, представленную на рис.3, как систему моделирования в системе пространство-время для объектов, движущихся относительно всех трех пространственных осей системы координат со скоростью 0<v<c.
Следует особо рассмотреть случай трансформации системы, когда все ее пространственные сектора и углы α’=β’=γ’=ζ’=η’=θ’ равны между собой (рис. 2). Данные углы можно вычислить, если отложить на каждой из осей равные отрезки, соединить их между собой и вписать полученный правильный тетраэдр в шар. В этом случае углы α’=β’=γ’=ζ’=η’=θ’ ≈109°28’.
В случае, когда все пространственные сектора равны между собой, можно найти собственную скорость движения объекта, при котором объект будет двигаться в данной системе. Равенство секторов в пространственно-временной системе становится возможным, когда собственная скорость объекта v≈0,8166 c. Это можно вычислить по изменению длины стержня в предложенной изменяемой системе координат.
Возникает предположение: при скорости около 0,8 скорости света, возможен процесс перехода объектов с пространственными характеристиками в систему с временной характеристикой и обратно, т.к. именно в этом состоянии отдельные части пространственно-временной системы стремятся к равенству и процесс перехода, из одной части рассмотренной системы в другую, менее затратен для трансформации объектов внутри рассматриваемой системы. Если же имеется возможность иметь в системе отсчета координату времени, то возможен и процесс движения относительно нее.
При разработке данной проблематики в математическом аппарате наблюдалось наличие рекурсивности (взаимная рекурсия) параметров пространственных характеристик и времени. Это предусматривает наличие в решении явно выраженных граничных условий.
Проекция описанной системы на плоскости может давать незначительную погрешность.
Заключение
Таким образом, аппарат для визуального моделирования процессов в системе пространство-время может представлять собой: систему, показанную на рис. 1, при условии, что собственная скорость объекта (скорость системы отсчета) равна нулю; систему, показанную на рис. 2, при условии, что скорость объекта близка к скорости света; систему, показанную на рис. 3, при условии, что скорость объекта больше нуля, но меньше скорости света. Выдвинуто предположение, что при скорости объекта равной около 0,8 скорости света, возможно, осуществить переход элементов из системы с пространственными характеристиками в систему с временной характеристикой.
Библиографическая ссылка
Петренко А.А. МОДЕЛИРОВАНИЕ В СИСТЕМЕ ПРОСТРАНСТВО-ВРЕМЯ // Международный журнал прикладных и фундаментальных исследований. 2015. № 5-2. С. 209-212;URL: https://applied-research.ru/ru/article/view?id=6712 (дата обращения: 28.02.2026).

