Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Черкашина Ю.А. 1

---

1 Национальный исследовательский Томский политехнический университет

Статья является результатом научных исследований сотрудников кафедры Прикладной математики Национального исследовательского Томского политехнического университета и сотрудников Сибирского государственного медицинского университета. Исследования посвящены применению математических методов для проведения процедуры распознавания состояния здоровья детей на основе медицинских данных гормонов крови. В статье подробно рассмотрена процедура неоднородной последовательной процедуры распознавания (НППР). Получены диагностические коэффициенты для отнесения объектов исследования к одному из непересекающихся классов (здоров, болен). Для применения НППР в задачах диагностики состояния организма сформировано две группы детей: обучающая и контрольная. Решение о наличии или отсутствии заболевания у детей контрольной группы определяется при использовании диагностического коэффициента. Приведены результаты исследования. Рассмотрены два примера использования диагностических коэффициентов отнесения объекта одному из двух классов.

Статья в формате PDF

1162 KB

неоднородная последовательная процедура распознавания

диагностические коэффициенты

диагностика

1. Гергет О.М., Кочегуров В.А. Решение актуальных медицинских задач математическими методами. – Томск: Изд-во ТПУ, 2002. – 145 c.

2. Гублер Е.В. Вычислительные методы анализа и распознавания патологических процессов. – Л: Медицина, 1978. – С. 296.

3. Дымова А.В., Лукина Е.Ю., Гергет О.М. «Диагностика мастопатии с помощью математических методов» V Международная студенческая электронная научная конференция «Студенческий научный форум». 15 февраля – 31 марта 2013 года – [Электронный ресурс]. Режим доступа – http://www.scienceforum.ru/2013/28/2326, свободный.

4. Марухина О.В. Алгоритмы обработки информации в задачах оценивания качества обучения студентов вуза на основе экспертно-статистических методов: Дис. ... канд. техн. наук. – Томск, 2003. – 164 с.

В последнее время в медицине все большее число исследователей занимаются проблемой диагностирования состояния здоровья детей. Известно, что предрасположенность человека к различным заболеваниям закладывается, в основном, в первый год жизни, поэтому актуальными являются задачи оценки состояния здоровья детей именно в этот период.

Проблемой выявления предпатологических и патологических изменений у грудных детей занимаются врачи, но в дополнение к специальным медицинским методам и подходам можно применять также и математические методы, алгоритмы и модели для оценки состояния здоровья детей [1].

Для постановки диагноза врачу приходится оперировать большим массивом разнородных данных и сложным комплексом методик. В связи с этим актуальной является задача по разработке дополнительных средств обработки показателей, характеризующих состояние детей, подозреваемых в заболевании и выдачи рекомендаций врачу.

Постановка диагноза на протяжении многих лет являлась в определенной мере искусством, помноженным на опыт и интуицию врача, и только с применением математических методов постановка диагноза может быть сформулирована, как математическая задача и автоматизирована.

Успешное решение задачи оценки состояния организма ребенка зависит от квалификации врача, однако современные компьютерные системы значительно ускоряют процесс обработки исходных данных и помогают поставить правильный диагноз.

Поэтому целью работы является обработка медицинских данных детей для оценки состояния их здоровья при помощи математических методов.

Математическая постановка задачи

При решении задач математической статистики существенную роль играет предположение о виде закона распределения наблюдаемой случайной величины Х. Методы математической статистики, основанные на этом предположении, называют параметрическими.

Однако у параметрических методов имеются существенные недостатки. Во-первых, на практике вид распределения наблюдаемой величины очень часто неизвестен. Во-вторых, экспериментальные данные при сборе и обработке информации почти всегда искажаются, что меняет их вид распределения. Поэтому, применяя параметрические методы в условиях такой априорной стохастической неопределенности, необходимо ясно осознавать, что расхождение между параметрической моделью и реальной ситуацией может привести к сильно искаженным или даже неверным результатам.

Следовательно, возникает необходимость в разработке таких статистических процедур, которые, с одной стороны, в ситуации, наиболее благоприятной для параметрических методов, почти не уступали бы им в эффективности, а с другой стороны, были бы малочувствительными к нарушению предположений, лежащих в основе параметрической модели.

Такие методы существуют. Они получили название непараметрических методов, так как не требуют знания закона распределения наблюдаемой случайной величины и используют лишь минимальную априорную информацию. Одним из важных плюсов непараметрических методов является возможность рассмотрение качественных признаков, которые выражаются порядковыми номерами или индексами.

Для отнесения всей совокупности объектов к одному из непересекающихся классов (болен, здоров) можно воспользоваться одним из непараметрических методов, а именно, неоднородной последовательной процедурой распознавания (НППР).

Являясь одномерной, НППР не требует использования сложных методов многомерной статистики. Она также не требует знания законов, которым подчинены эмпирические распределения, и пригодна при любой форме распределений [4]. Еще одним плюсом НППР является то, что данная процедура позволяет использовать неоднородные признаки, а именно, качественные (боль при осмотре, характер боли и т.д.) и количественные (показатели крови).

Для решения задач диагностики с помощью неоднородной последовательной процедуры распознавания следует сформировать две группы детей: обучающую и контрольную [3].

Введем диапазоны изменения показателей. Первый диапазон содержит в себе те значения, которые попадают в интервал, соответствующий медицинским показателям в пределах нормы, второй диапазон, значения, которые не попадают в данный интервал. Для каждого показателя существует своя граница нормы.

Для обучающей группы находятся диагностические коэффициенты по следующей формуле [2]:

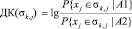, (1)

где σk,j – k-ый диапазон j-ого показателя, k = 1..3, j = 1...M;

xj – значение j-ого показателя;

A1 – событие наличия заболевания;

A2 – событие отсутствия заболевания;

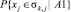– условная вероятность (вероятность события xj∈σk,j, при условии наступления события A1);

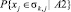– условная вероятность (вероятность события xj∈σk,j, при условии наступления события A2).

Вероятности, стоящие в числителе и знаменателе формулы (1) определяются следующими выражениями:

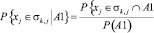. (2)

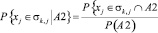. (3)

Решение о наличии или отсутствии заболевания у детей контрольной группы определяется при выполнении следующего неравенства:

ДКпор(А2) < ДК(σk,1) + ДК(σk,2) + … + + ДК(σk,N) < ДКпор(А1), (4)

где ДК(σk,j) – значение диагностического коэффициента k-ого диапазона, j-ого показателя.

Существование нескольких состояний (болен, здоров) предполагает наличие диагностических порогов, при достижении которых выносится решение. В неравенстве (4) пороговое значение для состояния A1 определяется как:

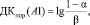(5)

для состояния A2:

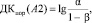(6)

где a – ошибка первого рода (объект из класса A1 можно отнести к классу A2);

β – ошибка второго рода (объект из класса A2 относят к классу A1).

Если сумма всех диагностических коэффициентов превысит пороговое значение ДК(А1) – у ребенка присутствует заболевание, если сумма окажется меньше порогового значения ДК(А2), ребенок считается здоровым. Если же сумма диагностических коэффициентов оказалась между пороговыми значениями, это означает, что данного ребенка следует обследовать более тщательно и полученной информации недостаточно для вынесения диагноза.

Таблица 1

Диагностические коэффициенты

Результаты исследования и их обсуждение

Исходная выборка включала 198 детей. Для определения здоров или болен ребенок сформировано две группы: обучающая – 132 ребенка и контрольная – 66 детей.

Диагностические коэффициенты, рассчитанные с использованием неоднородной последовательной процедуры распознавания, представлены в табл. 1. Для того чтобы установить диагноз ребенка из контрольной группы, необходимо в таблице найти значения диагностических коэффициентов, сложить коэффициенты и в зависимости от того, с какой стороны неравенства (4) оказалось значение, вынести решение, больна или здорова женщина.

Пороговые значения состояний «болен», «здоров» представлены в табл. 2.

Таблица 2

Пороговые значения

Рассмотрим пример использования диагностических коэффициентов для определения диагноза.

Исходные данные двух детей, один из которых здоров, второй имеет заболевание, представлены в табл. 3.

Таблица 3

Пример распознавания заболевания с использованием НППР

В примере 1 ребенок из тестовой выборки имел диагноз, поставленный врачом, – болен. Применяя НППР, сумма всех диагностических коэффициентов равна 4,92, это значение больше верхнего порогового значения ДК(А1) = 0,97. Следовательно, можно сделать вывод что ребенок в примере 1 болен. Состояние организма определено верно.

В примере 2 ребенок из тестовой выборки имел диагноз – здоров. Применяя НППР, сумма всех диагностических коэффициентов равна – 2,86, это значение меньше порогового, равного – 1,25, следовательно, можно сделать вывод: ребенок в примере 2 здоров.

Для оценки качества распознавания были проверены все дети из тестовой выборки. Качество распознавания с помощью неоднородной последовательной процедуры распознавания составило 81 %.

Заключение

Неоднородная последовательная процедура распознавания имеет большое значение и практическое применение в медицине. Процедура была апробирована на реальных медицинских данных, предоставленных медицинскими работниками. Рассмотрены два примера, демонстрирующие порядок использования НППР. Качество диагностирования, 81 % детей тестовой выборки был правильно отнесен к соответствующему классу, можно считать приемлемым.

Библиографическая ссылка