Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Орлова И.В. 1 Филонова Е.С. 1

---

1 Финансовый университет при Правительстве Российской Федерации (Финуниверситет)

В работе рассмотрен подход к построению модели множественной регрессии в условиях мультиколлинеарности данных. Рассмотрены типы мультиколлинеарности, причины возникновения и методы уменьшения или устранения ее. Данная статья посвящена рассмотрению и комбинированию различных методик отбора информативных факторов для регрессионного анализа. Предлагаемый подход реализован на основе реальных данных финансовой отчетности предприятий отрасли «Связь». Источник данных http://www.fira.ru/. В ходе решения поставленной задачи подробно показано использование теста Фаррара-Глоубера, пошаговой процедуры отбора факторов в модель, использование теста выбора «короткой» или «длинной» регрессии. Полученная модель была протестирована на мультиколлинеарность с помощью метода дополнительных регрессий (Тест VIF или метод инфляционных факторов). Результат тестирования показал, что полученная модель не содержит коллинеарных факторов и может быть использована для анализа и прогнозирования.

Статья в формате PDF

1223 KB

моделирование

мультиколлинеарность

кластерный анализ

модель множественной регрессии

тест Фаррара-Глоубера

метод инфляционных факторов

1. Гусарова О.М. Моделирование результатов бизнеса в менеджменте организации // В сборнике: Перспективы развития науки и образования сборник научных трудов по материалам Международной научно-практической конференции. – Тамбов, 2014. – С. 42–43.

2. Многомерный статистический анализ в экономических задачах: компьютерное моделирование в SPSS: Учебное пособие / Под ред. И.В. Орловой / Орлова И.В., Концевая Н.В., Турундаевский В.Б., Уродовских В.Н., Филонова Е.С. – М.: Вузовский учебник, 2009.

3. Орлова И.В. Линейная алгебра и аналитическая геометрия для экономистов: учебник и практикум для прикладного бакалавриата / И.В. Орлова, В.В. Угрозов, Е.С. Филонова. – М.: Издательство Юрайт, 2014 – 370 с. – Серия: Бакалавр. Прикладной курс.

4. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – 2-е издание, испр. и доп. – М.: Вузовский учебник: ИНФРА-М, 2012.

5. Орлова И.В., Концевая Н.В., Турундаевский В.Б., Уродовских В.Н., Филонова Е.С. Многомерный статистический анализ в экономических задачах: компьютерное моделирование в SPSS (учебное пособие) // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 3–2. – С. 248–250.

6. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование / учебное пособие для студентов высших учебных заведений, обучающихся по специальности «Статистика» и другим экономическим специальностям. – М., 2011. Сер. Вузовский учебник (3-е издание, переработанное и дополненное).

7. Орлова И.В., Половников В.А., Филонова Е.С., Гусарова О.М., Малашенко В.М., Дайитбегов Д.М. Эконометрика. Учебно-методическое пособие. – М., 2010.

8. Орлова И.В., Филонова Е.С. Эконометрическое моделирование финансовой эффективности предприятий, относящихся к виду экономической деятельности «Связь» // Международный бухгалтерский учет. – 2012. – № 43. – С. 22–24.

9. Орлова И.В., Филонова Е.С., Агеев А.В. Эконометрика. Компьютерный практикум для студентов третьего курса, обучающихся по специальностям 080105.65 «Финансы и кредит», 080109.65 «Бухгалтерский учет, анализ и аудит». – М., 2011.

10. Филонова Е.С. Состояние и тенденции финансовой эффективности предприятий отрасли (на примере предприятий отрасли «СВЯЗЬ»). В сборнике: Анализ современных проблем развития регионов Российской Федерации. – Орел, 2011. – С. 154–157.

Регрессионный анализ экономических переменных составляет основу эконометрических исследований. Хорошее уравнение регрессии может дать экономисту много важной информации об интересующем его экономическом объекте, а также даёт возможность прогнозирования показателей в зависимости от значений, влияющих на них факторов.

В регрессионном анализе многое зависит от выбора наиболее подходящего вида уравнения: линейное оно или нелинейное; если нелинейное, то какого именно вида. Но все же определяющим этапом исследования, предшествующим регрессионному анализу, являются процедуры, направленные на выбор факторов для уравнения регрессии. Рассмотрению и комбинированию различных методик отбора информативных факторов для регрессионного анализа посвящена данная статья.

При построении модели регрессии к факторам, включаемым в модель, предъявляется ряд требований:

1) каждый фактор должен быть обоснован теоретически;

2) в модель включаются только те факторы, которые могут быть количественно измерены или отождествлены с цифровыми метками (представлены в виде фиктивных переменных);

3) в модель нельзя включать совокупный фактор и факторы, его образующие;

4) факторы должны быть тесно связаны с исследуемой переменной;

5) факторы должны быть линейно независимы друг от друга.

Три последних требования можно коротко сформулировать так: факторы, включаемые в модель регрессии, должны быть тесно связаны с исследуемой переменной и слабо – с другими факторами модели.

При построении множественной линейной регрессии часто сталкиваются с наличием линейной или близкой к ней связи между всеми или некоторыми объясняющими переменными. Это явление называется мультиколлинеарностью. В математической статистике этот термин используется для обозначения тесной корреляционной взаимосвязи между отбираемыми для анализа факторами, совместно воздействующими на общий результат. Эта связь затрудняет оценивание параметров регрессии. Впервые на проблему мультиколлинеарности обратил внимание норвежский математик Нобелевский лауреат Рагнар Фриш [6].

В данной работе мы рассмотрим некоторые подходы к решению проблемы мультиколлинеарности экзогенных (объясняющих) факторов.

Мультиколлинеарность объясняющих переменных вызывает уменьшение точности оценивания или даже невозможность оценки влияния тех или иных переменных на результирующую переменную. Причина заключается в том, что вариации в исходных данных перестают быть независимыми и поэтому невозможно выделить влияние каждой независимой переменной в отдельности на зависимую переменную. Продемонстрируем это на простом примере. Пусть исследуется зависимость себестоимости от объема производства и введенных в действие основных фондов. Следует ожидать, что объем производства зависит также от основных фондов. Если мы обе переменные выберем в качестве объясняющих, то, очевидно, коэффициенты регрессии не будут точно отражать зависимость себестоимости от обоих факторов, так как основные фонды оказывают дополнительное влияние на себестоимость через объем производства.

Виды мультиколлинеарности: строгая (perfect) мультиколлинеарность – наличие линейной функциональной связи между независимыми переменными и нестрогая (imperfect) мультиколлинеарность – наличие сильной линейной корреляционной связи между независимыми переменными. Заметим, что корреляционные связи есть всегда. Проблема мультиколлинеарности – проблема силы проявления корреляционных связей.

Строгая мультиколлинеарность нарушает одно из основных условий теоремы Гаусса-Маркова [6] и делает построение регрессии невозможным. Нестрогая мультиколлинеарность затрудняет работу, но не препятствует получению правильных выводов.

Каковы основные причины возникновения мультиколлинеарности?

1. Ошибочное включение в уравнение двух или более линейно зависимых переменных.

2. В модели использованы факторные признаки, являющиеся составными элементами друг друга.

3. Исходные данные представлены временными рядами, имеющими одинаковые тенденции.

Мультиколлинеарность может проявляться и при отсутствии явных парных корреляционных зависимостей между переменными, так как мультиколлинеарность – ситуация линейной зависимости между объясняющими переменными. Однако вовсе необязательно эта зависимость должна быть парной.

При наличии мультиколлинеарности значимость отдельных коэффициентов регрессии уменьшается, так как стандартные ошибки становятся больше, что приводит к меньшей надежности полученных оценок.

Уменьшение значений t-статистики может выражаться в неверном с содержательной точки зрения знаке коэффициента регрессии. При мультиколлинеарности коэффициенты становятся неустойчивыми, поскольку в этом случае сложно отделить влияние одной переменной от влияния другой. Наличие доминантной переменной (коррелированной с зависимой переменной) делает коэффициенты при остальных объясняющих переменных незначимыми.

Выделим наиболее характерные признаки мультиколлинеарности:

1. Оценки становятся очень чувствительными к незначительному изменению результатов наблюдений и объёма выборки.

2. Оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой и обладает хорошей объясняющей способностью (хорошие значения F-статистики и коэффициента детерминации R2).

3. Оценки коэффициентов имеют неправильные с точки зрения теории (и логики) знаки или неоправданно большие значения. Коэффициенты, которые по логике должны быть значимы, оказываются незначимыми.

Для устранения или уменьшения мультиколлинеарности используется ряд методов.

Самый простой из них – исключение одной или нескольких переменных. При этом, какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании содержательных соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.

Другой метод устранения или уменьшения мультиколлинеарности заключается в переходе от несмещённых оценок, определённых по методу наименьших квадратов, к смещённым оценкам, обладающим, однако, меньшим рассеянием относительно оцениваемого параметра. Например, при использовании «ридж-регрессии» (или «гребневой регрессии») добавление τ (τ – некоторое положительное число, называемое «гребнем» или «хребтом») к диагональным элементам матрицы X`X делает оценки параметров модели смещёнными, но при этом увеличивается определитель матрицы системы нормальных уравнений. Таким образом, становится возможным исключение мультиколлинеарности в случае, когда определитель |X`X| близок к нулю.

Для устранения мультиколлинеарности может быть использован переход от исходных объясняющих переменных X1, X2,…, Xn, связанных между собой достаточно тесной корреляционной зависимостью, к новым переменным, представляющим линейные комбинации исходных. В качестве таких переменных берут, например, так называемые главные компоненты вектора исходных объясняющих переменных и рассматривают регрессию на главных компонентах, в которой последние выступают в качестве обобщённых объясняющих переменных, подлежащих в дальнейшем содержательной (экономической) интерпретации.

Можно применить преобразование мультиколлинеарных переменных:

– использовать нелинейные формы;

– использовать агрегаты (линейные комбинации нескольких переменных);

– использовать первые разности вместо самих переменных.

Рассмотрим конкретный набор данных и поставим задачу определения совокупности экзогенных переменных, наиболее подходящих для регрессионного анализа.

В качестве исходных данных будем использовать основные показатели баланса компаний-эмитентов, относящихся к сфере деятельности «Связь»[1] (всего 122 компании). Анализу показателей этой отрасли посвящены работы [8], [10].

В качестве результирующей (эндогенной) переменной выбираем показатель чистая прибыль (убыток) компаний.

В силу неоднородности объектов (компаний) была проведена их классификация на однородные группы методами кластерного анализа [2], [5]. В результате получены три кластера со следующими профилями (Кластерные профили – это, по сути, средние значения группирующих переменных в кластере):

1. Первый кластер самый большой – 109 компаний. Среди них много убыточных. Все показатели баланса предприятий этой группы на несколько порядков ниже, чем у других.

2. Второй кластер – 10 крупных прибыльных компаний.

3. Третий кластер – наименьший по количеству компаний, их всего три – Вымпел-Коммуникации (Билайн), Мобильные ТелеСистемы (МТС), Мегафон, но это самые крупные и самые прибыльные компании.

Объективную картину количественных взаимосвязей финансовых показателей предприятий данной отрасли можно получить, используя данные только о компаниях самого крупного первого кластера.

Краткая экономическая характеристика этих показателей:

– валюта баланса (ВБ) – это итог по всем счетам бухгалтерского баланса, сумма всех активов или всех пассивов компании;

– выручка (нетто) от продаж (ВП), дебиторская задолженность (краткосрочная) (ДЗ), запасы готовой продукции и товаров для перепродажи (ЗП), оборотные активы (ОА), основные средства (ОС), прибыль (убыток) от продаж (ПП), чистая прибыль (убыток) (ЧП) – это представители группы активов компании (здесь присутствуют как оборотные, так и внеоборотные активы);

– долгосрочные обязательства (ДО), краткосрочные обязательства (КО) – представители группы пассивов.

Схема отбора экзогенных факторов при решении данной задачи будет выглядеть следующим образом:

I. Корреляционный анализ данных, включая проверку теста Фаррара-Глоубера на мультиколлинеарность факторов;

II. Пошаговый отбор факторов методом исключения из модели статистически незначимых переменных;

III. При несоответствии результатов, полученных в пунктах 1) и 2), проверка теста на «длинную» и «короткую» регрессию.

I. Корреляционный анализ данных, включая проверку теста Фаррара-Глоубера [11] на мультиколлинеарность факторов

В табл. 1 представлена матрица коэффициентов парной корреляции для всех переменных, участвующих в рассмотрении.

Визуальный анализ матрицы позволяет установить:

● ЧП имеет довольно высокие парные корреляции со всеми переменными, кроме переменной ЗП (запасы готовой продукции и товаров для перепродажи) далее ее не будем рассматривать, что вполне объяснимо, так как предприятия отрасли «Связь» имеют специфическую продукцию;

● большинство переменных анализа демонстрируют довольно высокие парные корреляции, что обуславливает необходимость проверки факторов на наличие между ними мультиколлинеарности.

Для выявления мультиколлинеарности факторов выполним тест Фаррара-Глоубера по факторам ВП, ДЗ, ДО, КО, ОА, ОС, ПП, используя межфакторные корреляционные связи.

Проверка теста Фаррара-Глоубера на мультиколлинеарность факторов включает несколько этапов [6], [9] реализация которых представлена ниже.

1. Проверка наличия мультиколлинеарности всего массива переменных

● Найдем определитель матрицы межфакторных корреляций (табл. 2) R (det[R] = 0,0001) с помощью функции МОПРЕД. Определитель матрицы R близок к нулю, что позволяет сделать предположение об общей мультиколлинеарности факторов. Подтвердим это предположение оценкой статистики Фаррара-Глоубера.

Таблица 2

Матрица межфакторных корреляций R

● Вычислим наблюдаемое значение статистики Фаррара – Глоубера по формуле:

,

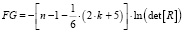где n = 109 – количество наблюдений (компаний); k = 7 – количество факторов (переменных анализа).

.

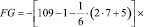
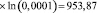Фактическое значение этого критерия FG сравниваем с табличным значением критерия χ2 с 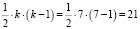степенью свободы и уровне значимости α = 0,05. Табличное значение χ2 = 32,64 можно найти с помощью функции ХИ2ОБР.

Так как FG > χ2 (953,87 > 32,67), то в массиве объясняющих переменных существует мультиколлинеарность.

2. Проверка наличия мультиколлинеарности каждой переменной с другими переменными.

Вычислим обратную матрицу R–1 с помощью функции Excel МОБР (табл. 3), диагональные элементы которой назовем cjj.

Таблица 3

Обратная матрица R–1

Вычисленные F-критерии

,

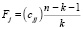где cjj – диагональные элементы матрицы R–1 приведены в (табл. 4).

Таблица 4

Значения F-критериев

Фактические значения F-критериев сравниваются с табличным значением Fтабл = 2,1 при v1 = 7 и v2 = n – k – 1 = = 109 – 7 – 1 = 101 степенях свободы и уровне значимости α = 0,05, где k – количество факторов. Так как все значения F-критериев больше табличного, то все исследуемые независимые переменные мультиколлинеарны с другими. Больше других влияет на общую мультиколлинеарность факторов фактор ВП – выручка (нетто) от продаж, меньше – фактор ДО – долгосрочные обязательства .

3. Проверка наличия мультиколлинеарности каждой пары переменных

Вычислим частные коэффициенты корреляции по формуле

,

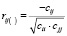где cjj – элементы матрицы R–1. Матрицу коэффициентов частной корреляции Rчастные, можно получить с помощью программ VSTAT, SPSS (табл. 5).

Таблица 5

Матрица коэффициентов частных корреляций Rчастные

В табл. 6 серым цветом выделены значения t-критерия, которые меньше табличного значения, а в табл. 5 –соответствующие им статистически незначимые коэффициенты частной корреляции. Жирным шрифтом цветом выделены значения t-критерия, которые больше табличного значения, и соответствующие им статистически значимые коэффициенты частной корреляции.

Вычисление t-критериев по формуле 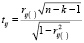(табл. 6).

Фактические значения t-критериев сравниваются с табличным значением tтабл = 1,98 при степенях свободы (n – k – 1) = 109 – 7 – 1 = 101 и уровне значимости α = 0,05.

Из табл. 6 и 7 видно, что две пары факторов ОА и ДЗ, ПП и ВП имеют высокую статистически значимую частную корреляцию, то есть являются мультиколлинеарными. Для того, чтобы избавиться от мультиколлинеарности, можно исключить одну из переменных коллинеарной пары. В паре ПП и ВП оставляем ПП, так как у нее меньше связи с другими факторами; в паре ОА и ДЗ оставим ОА, во-первых, с экономической точки зрения, а, во-вторых, так как у нее меньше значение F-критерия и, значит, она меньше влияет на общую мультиколлинеарность факторов.

Таким образом, в результате проверки теста Фаррара-Глоубера остается пять факторов: ДО, КО, ОА, ОС, ПП.

Завершая процедуры корреляционного анализа, целесообразно посмотреть частные корреляции выбранных факторов с результатом ЧП. В последнем столбце табл. 7 представлены значения t-критерия для столбца ЧП.

Таблица 7

Матрица коэффициентов частной корреляции с результатом ЧП

Таблицa 8

Фрагмент протокола пятифакторного регрессионного анализа

Из табл. 7 видно, что межфакторные частные корреляции слабые, а переменная ЧП имеет высокую и одновременно статистически значимую частную корреляцию только с фактором ПП (соответствующие значения в табл. 7 выделены жирным шрифтом).

Уточнение набора факторов, наиболее подходящих для регрессионного анализа, осуществим другими методами отбора.

II. Пошаговый отбор факторов методом исключения из модели статистически незначимых переменных

В соответствии с общим подходом, пошаговый отбор следует начинать с включения в модель всех имеющихся факторов, то есть в нашем случае с восьмифакторной регрессии. Но мы не будем включать в модель факторы из заранее известных коллинеарных пар (в связи с наличием коллинеарности ранее были исключены из рассмотрения ВП и ДЗ), а также фактор ЗП, имеющий слабую связь с ЧП. Таким образом, пошаговый отбор факторов начнем с пятифакторного уравнения. Фрагмент протокола пятифакторного регрессионного анализа представлен в табл. 8.

Статистически незначимыми (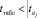) оказались три фактора (в табл. 8 они выделены жирным шрифтом). На следующем этапе пошагового отбора удаляем статистически незначимый фактор с наименьшим значением t-критерия, то есть фактор ОА (в табл. 8 выделен цветом).

Аналогично поступаем до тех пор, пока не получим уравнение, в котором все факторы окажутся статистически значимыми. Этапы получения такого уравнения, то есть фрагменты протоколов соответствующих регрессионных анализов, представлены в табл. 9 и 10.

Таблица 9

Фрагмент протокола четырехфакторного регрессионного анализа

Таблица 10

Фрагмент протокола трехфакторного регрессионного анализа

Из табл. 10 видно, что уравнение с тремя факторами ОС, ПП и КО обладает статистически значимыми коэффициентами перед факторами (в нем незначим только свободный член), а, значит, и сами эти факторы статистически значимы.

Таким образом, в результате пошагового отбора получено трехфакторное уравнение регрессии, все коэффициенты которого (кроме свободного члена) значимы при 5 %-ном уровне значимости, вида

Y = –4456,7 – 0,038·Х1 + + 0,647·Х2 + 0,072·Х3,

где Y – ЧП, – ОС, – ПП, – КО.

III. Проверка теста на «длинную» и «короткую» регрессии

По результатам пунктов 1) и 2) возникает необходимость выбора из двух регрессий: «длинной» – с тремя факторами (ОС, ПП и КО) и «короткой» – с одним фактором (ПП).

Воспользуемся тестом на «длинную» и «короткую» регрессии [6]. Этот тест используется для отбора наиболее существенных объясняющих переменных. Иногда переход от большего числа исходных показателей анализируемой системы к меньшему числу наиболее информативных факторов может быть объяснен дублированием информации, из-за сильно взаимосвязанных факторов. Стремление к построению более простой модели приводит к идее уменьшения размерности модели без потери её качества. Для этого используют тест проверки «длинной» и «короткой» регрессий.

Рассмотрим две модели регрессии:

yi = β0 + β1 xi1 +…+ βk xik + ε i (длинную),

yi = β0 + β1 xi1 +…+ βk xik-q + εi (короткую).

Предположим, что модель не зависит от последних q объясняющих переменных и их можно исключить из модели. Это соответствует гипотезе

H0: βk-q+1 = βk-q + 2…= βk = 0,

т.е. последние q коэффициентов βi равны нулю.

Алгоритм проверки следующий:

– Построить по МНК длинную регрессию по всем факторам X1, …, Xk и найти для неё сумму квадратов остатков – ESSдлин.

– Построить по МНК короткую регрессию по первым (k – q) факторам X1, …, Xk–q и найти для неё сумму квадратов остатков – ESSкор.

– Вычислить F-статистику

.

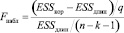– Если Fнабл > Fтабл (α, v1 = q, v2 = n – k – 1), гипотеза отвергается (выбираем длинную регрессию), в противном случае – выбираем короткую регрессию.

На основании данных нашего примера сравним две модели: «длинную» (с факторами X1, X2, X3) и «короткую» (только с фактором X2).

1. Построим длинную регрессию по трем факторам X1, X2, X3 и найдем для неё сумму квадратов остатков – ESSдлин (табл. 11).

Таблица 11

Фрагмент протокола регрессионного анализа для длинной (трехфакторной) регрессии

2. Построим короткую регрессию по одному фактору X2 и найдем для неё сумму квадратов остатков – ESSкор (табл. 12).

Таблица 12

Фрагмент протокола регрессионного анализа для короткой (однофакторной) регрессии

3. Вычислим F-статистику

,

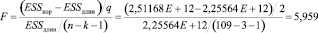Fтабл(0,05; 109 – 3 – 1 = 105) = 3,083.

4. Так как F > Fтабл, отдаем предпочтение длинной регрессии

Y = –4456,7 – 0,038·Х1 + + 0,647·Х2 + 0,072·Х3.

Набор факторов в этой модели вполне соответствует результатам проверки теста Фаррара-Глоубера.

Протестируем полученную модель на мультиколлинеарность с помощью метода дополнительных регрессий (Тест VIF или метод инфляционных факторов).

Для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:

,

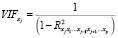где 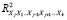– это значение коэффициента множественной детерминации, полученное для регрессора Xj как зависимой переменной и остальных переменных. При этом степень мультиколлинеарности, представляемая в регрессии переменной Xj, когда все переменные X включены в регрессию, есть функция множественной корреляции между Xj и другими переменными X.

Если 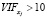, то считается, что данный регрессор приводит к мультиколлинеарности.

Расчеты были выполнены с помощью программы Gretl, хотя сложность расчетов невелика и это вполне можно было вычислить в Excеl. В нашем случае мы получили следующие VIF значения:

,

,

.

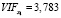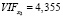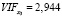Так как все VIF значения меньше 10, то можно сделать вывод, что построенная модель Y = –4456,7 – 0,038·Х1 + 0,647·Х2 + + 0,072·Х3 не содержит коллинеарных факторов и может быть использована для анализа и прогнозирования. Тем самым, поставленная задача выбора факторов в модель регрессии решена.

Библиографическая ссылка