Как известно, реальные механические системы, помимо традиционно общих, всегда учитывающих параметров протяженности и вещественности, характеризуются так называемыми реальными параметрами, которые имеют различную физическую природу, а именно:
– все реальные звенья и связи нелинейны;
– многие реальные схемы имеют дефекты, конструкторские ошибки;
– все реальные системы имеют первичные ошибки изготовления и сборки;
– все реальные системы при эксплуатации имеют силовые ошибки (деформации), перекладки зазоров в связях;
– все реальные системы имеют температурные ошибки;
– реальные системы могут иметь запредельные режимы эксплуатации.
Реальные параметры вызывают ошибки механических систем.
Ошибка положения механизма – разность координат положения выходного (исполнительного) звена действительного и идеального механизмов при одинаковом положении ведущего. Ошибки скорости и ускорения есть производные от ошибок положения. Эти ошибки вызывают дополнительное динамическое нагружение звеньев и связей и обуславливают вторичные динамические ошибки системы. Перекладка зазоров в меняющихся направлениях силовых связей звеньев системы порождает динамические удары в связях с известными последствиями для их работоспособности и виброактивности.
Первичные, силовые, температурные ошибки неизменно превращают теоретически плоскую механическую систему в пространственную с неопределенностью распределения нагрузок в связях, а после перекосной выборки зазоров в связях возникает паразитное контурное силовое нагружение кинематической цепи с крайне неблагоприятным, нерасчетным режимом ее функционирования.
Полная модель первичных ошибок должна учитывать ошибки угловых размеров, погрешности формы звеньев и связей (неплоскостность, выпуклость, вогнутость, некруглость, погрешности шагов винтов, зубчатых колес, шлицев и т.д.). Ужесточение требований к точности ведет к удорожанию технологии, но не решает проблем функционирования реальных систем.
Цель исследования. В настоящее время объективно сформировались два различных принципа конструирования механических систем.
Первый основан на математических расчетных моделях высокой степени достоверности, содержащих возможно полное знание и учет физических процессов, протекающих в машине, точное знание уровня и характера силового нагружения звеньев и связей, учет реальных параметров системы, свойств материалов, условий эксплуатации.
Второй – статистический принцип конструирования основан на неполном знании реальных параметров объекта, которое компенсируется корректирующими коэффициентами при определении расчетных нагрузок и при выборе допускаемых напряжений. Эти коэффициенты выбирают из справочной литературы, статистически обобщающей опыт создания и эксплуатации, близких по типажу и режимам эксплуатации систем.
В [1] был предложен принцип конструирования, в основе которого содержится прием наделения проектируемой системы на стадии проектирования свойством ее адаптации к реальным параметрам конструкторскими и технологическими средствами.
Вся совокупность механических систем с адаптивными свойствами, построенных на основании общих признаков, отражающих особенности их строения, может быть представлена четырьмя группами. Рассмотрим более подробно первую группу: это системы (механизмы), имеющие приспособленные формы движения. Это механизмы, которые могут содержать упругие и гибкие звенья в качестве силовых элементов, одновременно выполняющих функции компенсаторов неопределенностей.
Метод исследования. Корректировка состава связей конкретной механической системы для достижения определенности базирования всех звеньев, исключения контурных и локальных связей, а также решения прямой задачи структурного синтеза схем механизмов с оптимальной структурой могут быть проведены на основе алгебраического метода, разработанного С.Н. Кожевниковым и построенного на учете двух факторов: заданных подвижности механизма и преобразования исходного вида движения в необходимое выходное движение [2].
Из [2] находим общее количество возможных (разрешенных) движений в связях:
f = f0 + fx, (1)
где f0 – количество движений основных (связанных со стойкой) звеньев; fx – количество возможных движений в промежуточных связях.
Общее количество звеньев будет определяться:
n = n0 + nx +1, (2)
где n0 – количество звеньев, связанных подвижно со стойкой (количество основных звеньев); nx – количество промежуточных звеньев.
Общее количество замкнутых контуров определяется:
k = k0 +kx, (3)
где k0 – количество контуров, в состав которых входят основные звенья; kx – количество контуров, образуемых промежуточными звеньями.
Подвижность механизма в этом случае будет определяться:
W = f – 6k +q, (4)
где q – количество избыточных связей.
Зависимость (4) предполагает, что контур накладывает на кинематическую цепь шесть связей и для оптимальной структуры q = 0 (4) запишется как:
W = f – 6k или W = f0 + fx – 6k (5)
Количество контуров, в которые входят основные звенья:
k0 = n0 – 1. (6)
Так как
k = k0 + kx, то kx = k – n0 +1, (7)
Общее количество связей будет: p = p0 + px, откуда
px = p – n0. (8)
Количество пар и количество звеньев в кинематической цепи связаны соотношением:
p = n + k – 1.
Для примера, рассмотрим оригинальную часть пространственного манипулятора [2, 3], реализующую угловые движения вокруг осей X и Y и поступательное перемещение вдоль оси Z за счет сложения двух встречных вращений [4] (рис. 1).
В шарнирном соединении d номинально необходимая подвижность равна единице (рис. 2).
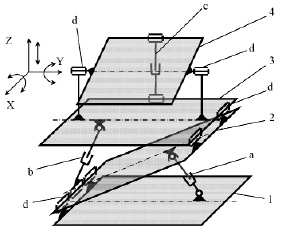
Рис. 1. Схемное решение пространственного манипулятора: 1 – поворотный стол; 2 – наклонная платформа; 3 – опорно-поворотное устройство; 4 – установочное звено (рабочий стол); a, b, c – приводные устройства (гидроцилиндры, шарико-винтовая передача); d – шарнирное соединение платформ
Рис. 2. Схема со связями V класса
По формуле для пространственной связи подвижного звена, подвижность будет:
W = 6n – 5p5 = 6·1 – 5·2 = – 4,
т.е. Для исключения избыточных связей кинематической цепи необходимо добавить пять движений. Сделав замену, по рис. 2, двух кинематических пар пятого класса – одной третьего, а другую второго класса получим комбинацию связей на рис. 3.
Тогда подвижность будет:
W = 6·1 – 5·0 – 4·0 – 3·1 – 2·1 – 0 = 1.
Фрагмент пространственного манипулятора на рис. 4 и рис. 5 имеет рациональную структуру.
Рис. 3. Схема с рациональным выбором связей
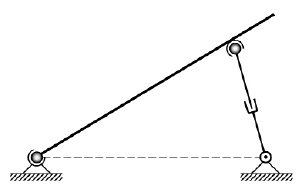
Рис. 4. Схема манипулятора с рациональным выбором связей в плоскости
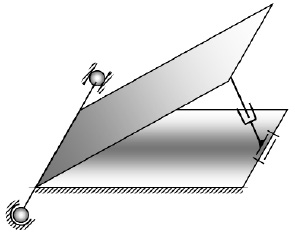
Рис. 5. Схема манипулятора с рациональным выбором связей в пространстве
Подвижность кинематической цепи будет:
W = 6·3 – 5·1 – 4·1 – 3·2 – 2·1 – 0 = 1.
Выводы
Таким образом, техническое решение реального пространственного манипулятора с промежуточным звеном и оптимальной структурой должно предусматривать использование в качестве одной из промежуточных пар вместо традиционной одноподвижной пары кинематического соединения, разрешающего пять движений, что в принципе может быть технически реализовано, когда любая пара, например А, исполняется самоустанавливающимся подшипником скольжения или качения, а в опоре В такой подшипник имеет дополнительное линейное движение (рис. 3).
Библиографическая ссылка
Балакин П.Д., Шамутдинов А.Х. ВЫБОР РАЦИОНАЛЬНЫХ ГЕОМЕТРИЧЕСКИХ СВЯЗЕЙ ДЛЯ СИНТЕЗА ОРИГИНАЛЬНОЙ ЧАСТИ ПРОСТРАНСТВЕННОГО МАНИПУЛЯТОРА // Международный журнал прикладных и фундаментальных исследований. 2015. № 5-3. С. 374-378;URL: https://applied-research.ru/ru/article/view?id=6790 (дата обращения: 27.02.2026).

