Линейное алгебраическое уравнение можно определить как уравнение, в которое искомые неизвестные входят в первой степени и между собой не перемножаются, т.е. в левой части линейного уравнения обычно записывается линейная комбинация искомых неизвестных, а в правой – свободный член. Совокупность таких уравнений образует систему линейных алгебраических уравнений (СЛАУ). Если СЛАУ имеет единственное решение, то она называется определённой. В случаях, когда решений бесконечное множество, СЛАУ называется неопределённой. Для решения определенных СЛАУ применяют методы Крамера, Гаусса, матричный, численные методы. Для неопределённой СЛАУ можно находить общее решение и какие-либо частные решения из их бесконечного множества.
В соответствии с ФГОС раздел «Линейная алгебра» модуля «Математика 1» входит в рабочие программы всех унифицированных образовательных математических кластеров дисциплины «Математика» [1]. В рабочие программы в обязательном порядке включаются индивидуальные домашние задания (ИДЗ) по всем разделам, в том числе и по разделу «Линейная алгебра». Решение СЛАУ «вручную» требует много времени, большого внимания, довольно громоздких преобразований и вычислений. Если допущена ошибка в решении СЛАУ, её бывает нелегко обнаружить. Целью применения пакета Mathcad в учебном процессе явилась потребность использования возможностей компьютеров для решения СЛАУ.
Квадратные СЛАУ с невырожденной основной матрицей системы, а также матричные уравнения в среде пакета Mathcad легко решаются матричным методом. Например, чтобы решить СЛАУ
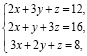
достаточно задать основную матрицу системы
,
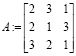столбец свободных членов
,
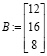записав произведение обратной матрицы A–1 на матрицу В и воспользовавшись клавишей «=», получить решение:
.
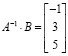Проверка правильности решения также осуществляется в одно действие умножением матрицы А на найденную матрицу решения:
.
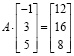Можно предварительно записать найденную матрицу
.
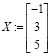решения СЛАУ, тогда для проверки потребуется ввести с клавиатуры произведение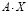 
и клавишу «=»:
.
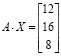Начиная с шестой версии Mathcad, квадратные СЛАУ с невырожденной матрицей можно решать, используя встроенную функцию lsolve(A,B): X:= lsolve(A,B), и сразу получить решение
.
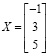Для решения неопределенных СЛАУ в среде пакета Mathcad имеется несколько возможностей. Версия Mathcad 13/14 (в предыдущих версиях Mathcad основная матрица СЛАУ должна быть квадратной) позволяет находить одно из бесконечного множества частных решений СЛАУ при помощи встроенной функции lsolve(A,B) [2]. Например, так:
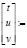lsolve
,
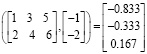если решается СЛАУ
.
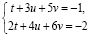Замена знака равенства стрелкой из палитры символьных операций Symbolic возвращает частное решение в виде рациональных чисел:
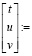lsolve
.
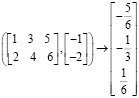Но общее решение, применяя встроенную функцию lsolve(A,B), найти не удается.
Получить общее решение СЛАУ можно директивой solve палитры символьных операций Symbolic. Для этого надо в левую метку директивы solve записать матрицу из одного столбца и таким количеством строк, сколько уравнений в СЛАУ, отделяя свободные члены равенствами из палитры Boolean или вводя знаки «=» с клавиатуры вместе с клавишей Ctrl (получается «жирный» знак равенства). В правой метке следует перечислить имена всех неизвестных СЛАУ. Например,
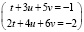solve,t,u,v 
.
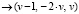Возвращается общее решение, в котором t, u – базисные неизвестные, v – свободная неизвестная. Частное решение, возвращаемое встроенной функцией lsolve(A,B), соответствует свободной неизвестной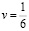 
.
Недостаток применения директивы solve заключается в том, что в рассматриваемом примере базисные неизвестные выбираются единственным образом, хотя в качестве базисных неизвестных можно выбрать любую другую пару неизвестных, т.к. в рассматриваемом примере все миноры второго порядка основной матрицы системы отличны от нуля.
Обойти проблему можно, применяя предлагаемый наиболее близкий к классическому исследованию и решению СЛАУ алгоритм.
Ввести основную матрицу СЛАУ, обозначив ее A, например. В задаче исследовать СЛАУ на совместность задать расширенную матрицу системы А1.
Ввести столбец свободных членов, обозначив его, например, В.
Найти ранг основной матрицы системы: rank(A). Для СЛАУ больших размеров найти rank(A1). Если rank(A)≠rank(A1), СЛАУ несовместна, т.е. решений не имеет, и на этом исследование и решение СЛАУ заканчивается.
Если rank(A) = rank(A1), выбрать отличный от нуля базисный минор F (порядок базисного минора равен рангу основной матрицы СЛАУ) и базисные неизвестные, коэффициенты при которых вошли в базисный минор.
Оставшиеся свободные неизвестные перенести к свободным членам и ввести получившийся столбец С как функцию свободных неизвестных.
Получить общее решение, умножив обратную матрицу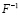 
на матрицу С.
Присвоив свободным неизвестным числовые значения, получить соответствующее частное решение.
Для проверки надо матрицу А умножить на матрицу-столбец В1 решения, составленного из свободных и базисных неизвестных или из значений неизвестных частного решения.
Применение алгоритма рассмотрим на предыдущем примере
.
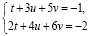1. 
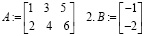
3. rank(A)=2
4. Выберем базисными неизвестными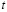 
и 
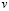. Тогда
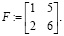
Определитель матрицы F отличен от нуля: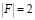 
.
5. Составим матицу С:
.
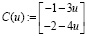6. Получим общее решение
.
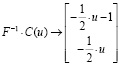7. Пусть свободная неизвестная
.
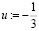При этом значения базисных неизвестных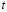 
и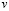 
получатся умножением
.
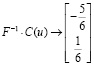8. Составим столбец
.
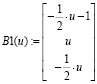Тогда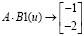 
,
или сделаем проверку для частного решения:
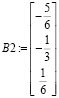
и получим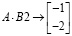 
.
Преимущества предлагаемого алгоритма заключаются в том, что решение СЛАУ осуществляется не формально, когда возвращается единственный вариант ответа. В процессе реализации алгоритма исследуются основные свойства СЛАУ: ранги основной и расширенной матриц системы, выбираются базисные неизвестные и свободные неизвестные, возвращаются общие решения при любом допустимом наборе базисных и свободных неизвестных. Заменяя столбцы основной матрицы СЛАУ столбцом свободных членов со свободными неизвестными, можно получать общее решение и методом Крамера, о чём в учебной литературе упоминаний нет. Вот как это можно осуществить для СЛАУ
,
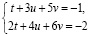решенной выше матричным методом:
;
.
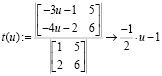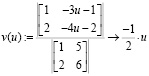Таким образом, методом Крамера получено общее решение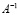 
.
Библиографическая ссылка
Тарбокова Т.В. РЕШЕНИЕ НЕОПРЕДЕЛЕННЫХ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В СРЕДЕ ПАКЕТА MATHCAD // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 6-2. – С. 362-365;URL: https://applied-research.ru/ru/article/view?id=6907 (дата обращения: 21.11.2024).