Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Уалиев З.Г. 1 Уалиев Г. 1 Уалиева И.М. 2

---

1 Казахский национальный педагогический университет им. Абая

2 Международный университет Информационных технологий (МУИТ)

В статье рассматриваются вопросы движения механизмов с упругим шатуном. Получены математические выражения для определения упругих перемещений шатуна. Показана зависимость угла поворота ведомого звена от изменения длины шатуна.

Статья в формате PDF

938 KB

математическое моделирование

двухкоромысловый механизм

упругий шатун

1. Бать И. Уравнение движения плоского четырехзвенника с упругим промежуточным звеном // Труды семинара по ТММ, 1957.

2. Уалиев Г., Уалиев З.Г. Математическое моделирование динамики механических систем нелинейными характеристиками. – Алматы, 2007. – 332 с.

3. Джолдасбеков У.А., Уалиев Г.У. Совершенствование механизмов ткацких станков СТБ. – М.: Легпромиздат, 1986. – 192 с.

Рассмотрим движения плоского механизма, у которого шатун имеет конечное упругое перемещение (растяжение и сжатие). Например, механизмы прокладывания уточной нити ткацких станков типа СТБ, такие как боевой механизм, четырехцветный и шестицветный механизм смены утка, механизм торможения прокладчика представляют собой кулачково-рычажные механизмы с упругими звеньями и связями. Рабочий процесс в этих механизмах осуществляется за счет потенциальной энергии закрученного вала или сжатых цилиндрических пружин.

В плоском четырехзвенном механизме (рис. 1) упругий шатун жесткостью с может быть рассмотрен как и нестационарная связь, поскольку относительное перемещение точек А и В двух различных звеньев зависит от величины силы, действующей вдоль упругого шатуна.

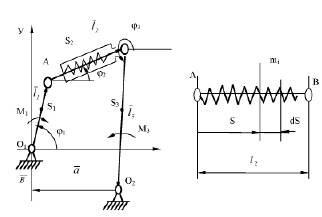
Рис. 1 . Двухкоромысловый механизм с упругим шарниром

Математическое выражение деформации упругого звена позволяет объединить в одну систему уравнения движения твердых тел, расположенных по обе стороны упругого звена. Задача в этом случае будет сведена к отысканию основного движения кривошипа и коромысла как системы твердых тел, и дополнительного движения, определяемого упругой характеристикой шатуна. Нами получено дифференциальное уравнение для определения перемещения упругого шатуна в виде:

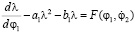, (1)

где 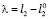– изменение длины шатуна.

Из уравнения (1), как частный случай, получится известное выражение для малых упругих перемещений [1]. Получена система уравнений, описывающая движение двухкоромыслового механизма с упругим шатуном в виде:

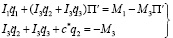, (2)

где

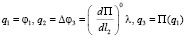(3)

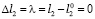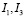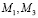«0» положение при , и – моменты инерции и моменты сил. Если считать, что ведущее звено вращается с постоянной угловой скоростью 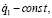– то движение описывается уравнением

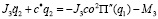, (4)

где 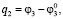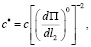П – функция положения.

На основе разработанной методики рассматриваются вопросы построения моделей механизмов прокладывания уточной нити и исследования движения механизмов с учетом упругости звеньев. Механизм подачи и прокладывания уточных нитей станков СТБ (ткацких станков) представляют из себя плоские и пространственные кулачково-рычажные механизмы переменной структуры с упругими звеньями и связями. В них за один цикл работы изменяются вид механизмов, ведущие звенья, число степеней свободы и подвижных звеньев, характер упругих звеньев и связей и др. поэтому выбор расчетных схем механизмов и составление их математических моделей проведены с учетом структуры и характера осуществляемого ими движения.

На рис. 2 представлена конструктивная схема механизма смены цвета утка станков-автоматов СТБ и его расчетная схема, представляющая из себя, соединение двух коромысловых механизмов с упругими шатунами.

На рис. 3. представлены динамические модели механизма смены цвета при сжатии и расжатии пружин.

Процесс смены цвета осуществляется за счет расжатия пружин. Движение системы происходит под действием моментов упругих сил 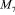и 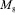со стороны аккумуляторов-пружин 5 и 6.

За обобщенные координаты примем углы поворота трехплечих рычагов 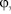и 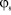от вертикального положения. Функции положения и передаточные функции используем из работы [2].

Обобщенные силы упругих сил и сил сопротивления определяются из равенств

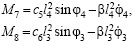(5)

Считая, что центры тяжести трехплечих рычагов находятся в точке О, суммирующего рычага в точке С, приведенный к звену 14 момент инерции нижней (правой) части постоянный и, пренебрегая вращательным движением тяги, для кинетической энергии системы получим следующее выражение:

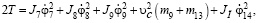(6)

где

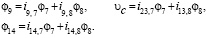
Подставив их в (6), получим

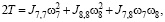
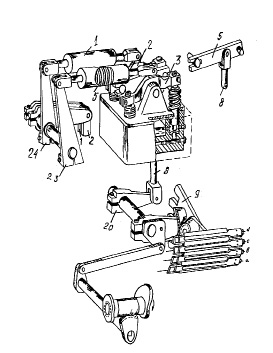
Рис. 2. Конструктивная схема механизма смены цвета станков-автоматов СТБ

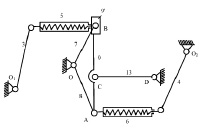
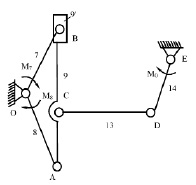
Рис. 3. Расчетная схема механизма в процессе сжатия и растяжения пружин

где

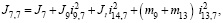
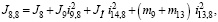
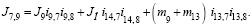
Тогда уравнения движения механизма примут следующий вид

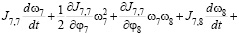
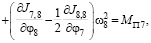
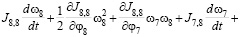
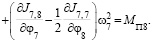(7)

где 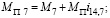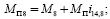МП – приведенный момент сил тяжести звеньев, нижней части механизма.

Во многих системах возникает необходимость учета массы деформируемого звена. Это связано с тем, что упругое звено имеет массу того же порядка или даже больше, чем жесткие звенья, и как следствие, оно является источником инерционных возбуждающих сил. Например, в механизмах смены цвета утка ткацких станков [3] движение осуществляется за счет деформации (сжатие-растяжение) упругого шатуна, причем его масса больше массы кривошипа и коромысла. Показано, что кинетическая энергия упругого шатуна определяется из выражения

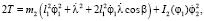
где 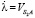– составляющая относительной скорости точки 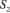вдоль шатуна; b – угол между векторам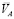и и 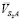; I2 – переменный момент инерции шатуна.

Получена система уравнений, описывающая движение плоского четырехзвенного механизма с учетом масс упругого шатуна в виде:

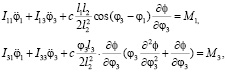(8)

где 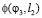– уравнение связи.

Решением систем уравнений (2) определяются законы движения двухкоромыслового механизма при известном перемещении (деформации) центра тяжести упругого звена, определяемого из уравнения (1). Указанные законы движения, для периодов сжатия и разрядки, определяются из систем уравнений (8) с учетом массы упругого шатуна.

Библиографическая ссылка