Особая актуальность данной публикации продиктована тем, что для установления абсолютной давности выполнения реквизитов документов, в рамках производства судебно-технических экспертиз документов, при проведении расчетов используется математическое моделирование, позволяющее определить «возраст» штрихов исследуемых реквизитов. Например, в исследовательской методике «Способ определения давности выполнения реквизитов в документах по относительному содержанию в штрихах летучих растворителей», разработанной РФЦСЭ при Минюсте России, декларируется, что при моделировании процесса старения исследуемых штрихов в проверяемый период времени, «за основу принимают модель темнового старения при комнатной температуре штрихов красящего вещества того же рода (вида), что и в исследуемых штрихах, имеющего тот же (или близкий состав основных компонентов (растворителей и красителей). Исследуют уменьшение относительного содержания конкретного растворителя в штрихах-моделях. Объекты исследования: экспериментальные штрихи, штрихи – образцы сравнения (если представлены эксперту) с известным временем выполнения» [1, 2, 3].
Аналогичный подход используется и в методике «Установление абсолютной давности выполнения реквизитов документов по динамике выцветания цветовых штрихов», разработанной специалистами ООО Экспертное учреждение «Воронежский Центр Экспертизы», где расчет «возраста» штрихов опытных (исследуемых) объектов проводится путем изучения модели процесса изменения цветовых параметров этих штрихов в принятом цветовом пространстве, с учетом аналогичных процессов выцветания контрольного штриха с известным временем нанесения, выполненного материалом письма того же типа, что и опытный. При этом в основе расчетов лежит доказанная закономерность изменения цветовых параметров штриха во времени [7], а основным критерием подбора красящего вещества для контрольного штриха является его сопоставимость с опытным по спектральным параметрам (что, в свою очередь, является прямым отражением компонентного состава материала письма).
Различие в общих подходах указанных методик, по сути, состоит лишь в выборе «значимого параметра», используемого при расчетах, а так же в принципах использования соответствующих штрих-моделей – в методике РФЦСЭ применяются штрихи, выполненные на листах бумагах в проверяемый период времени, хранящиеся в коллекции, а согласно методики ООО ЭУ «ВЦЭ», контрольный штрих наносят подобранным материалом письма на свободный участок листа бумаги документа в непосредственной близости с опытным объектом в начальный период основного исследовательского этапа, что обеспечивает схожие условия хранения опытных и контрольных объектов в процессе исследования.
При этом следует выделить важное обстоятельство. Результаты анализа материалов многочисленных экспертных исследований, проведенных разными экспертными организациями по указанной методике РФЦСЭ, позволяют утверждать, что проблема моделирования процессов старения, по результатам чего эксперты приходят к выводам о давности выполнения реквизитов, на сегодняшний день не решена. Методические рекомендации, разработанные сотрудниками РФЦСЭ, в части касающейся процесса моделирования, носят общий декларативный характер, не содержат подробного и четкого описания, и, более того, имеют сущностные ошибки, исключающие саму возможность получения достоверных результатов. О чем будет подробно описано ниже.
Математическое описание степенной функции как закономерности процесса, зависящего от времени
При изучении свойств материалов письма, ряд процессов, зависящих от изменения какого-либо параметра во времени, можно описать уравнением сложной функции вида:
.
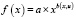Из классического определения, функция – это математическое понятие, отражающее связь между элементами множества, это правило, по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений). Буква x, которая обозначает каждый элемент множества f(x) называется независимой переменной или аргументом функции. Ее физический смысл состоит в отсчете момента времени без относительно астрономического исчисления. Иными словами, это условная ед. времени (единичный временной интервал) – сутки, неделя, год.
Элемент y = f(x), соответствующий конкретному элементу x – частному значению функции в точке x. Множество Y = f(X) называется также областью значений функции.
Для рассматриваемой прикладной области значение параметра a есть величина, вычисляемая априорно для каждого рассматриваемого случая, а значение функции g(x,u) изменяется в зависимости от конкретных условий. Значение параметра u индивидуально для каждого конкретного случая.
При этом величина параметров a и f(X) имеют одинаковую размерность.
Область определения степенной функции зависит от значения показателя степени. Степенная функция задается формулой вида y = axb.
Критерии моделирования процесса старения штриха как зависящего от уменьшения измеряемого параметра во времени
Согласно [1, 2] суть предлагаемой методики в выборе критерия оценки признака старения – концентрации растворителя в определенный момент времени и принципы моделирования процесса старения на основе данных о величинах концентрации растворителя, полученных от штрихов-аналогов и исследуемых штрихов.
В качестве признака старения штриха выбрано уменьшение относительного содержания растворителя в штрихе – количества растворителя, приходящегося на массу красящего вещества в штрихе C. Процесс естественного старения штрихов, имеющих одинаковую конфигурацию, характеризующихся одинаковым распределением красящего вещества в штрихах, удовлетворительно описывается уравнением степенной функции:
,
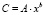где x – возраст штриха на момент начала исследования;
значения коэффициента A и показателя степени b находят в результате анализа статистических данных о процессе старения штрихов, выполненных красящим веществом конкретного рода, вида, рецептуры».
Таким образом, в анализируемой методике, содержание растворителя является значимым измеряемым параметром и имеет размерность – масса/объем (концентрация).
Согласно методики, после проведения газо-жидкостного хроматографирования экстрактов вырезок штрихов «За характеристику содержания растворителя в штрихе принимают высоту соответствующего пика на графической зависимости – хроматограмме штриха, выраженную в условных единицах (hp) с учетом вклада продуктов термодесорбции из бумаги (Δh) …» [1]. В статье [2] эти условные единице предлагается оценивать в мВ, что также по сути не является единицами измерения концентрации.
То есть, фактически это величина (hp) выраженная или в у.е., либо в мВ, или в любых единицах детектирующей шкалы, характеризующий отклик детектора, и к численному значению величины концентрации не имеет прямого отношения.
Чтоб перейти от величин отклика детектора в условных единицах hp к величинам концентрации необходимо провести так называемую калибровку применяемой хроматографической системы. Она может представлять один из нескольких методов, подробно описанных в специальной литературе, посвящённой разделительной количественной хроматографии [4].
В противном случае, равно как и в предлагаемом авторами, эта величина (hp), так и останется величиной условных единиц отклика детектора.
Из теории разделительной колоночной хроматографии известно, что различные по своей «компоновке» хроматографические системы, а именно имеющие различные технические параметры, такие как:
– «мертвый» объем хроматографической системы;
– геометрия разделительной колонки;
– физико-химическая природа сорбента;
– объем вводимой пробы, и т.д.
будут давать различные времена удерживания выделяемого компонента. Наконец, просто продолжительность времени использования данной разделительной колонки будет приводить к изменению селективности разделительной системы и изменении времени удерживания выделяемого компонента. Без тестирования используемой в данный момент хроматографической системы на время удерживания выделяемого компонента с использованием контрольного раствора и приведения полученной хроматограммы как подтверждения времени удерживания выделяемого компонента (в данном случае растворителя), говорить о том, что определяется именно то вещество, которое декларируется нельзя [5].
Согласно [1], за характеристику массы красящего вещества в пробе (в штрихе) может быть принята любая характеристика штриха, пропорциональная массе красящего вещества в пробе. Оценку «возраста» штрихов исследуемых реквизитов проводят по характеру уменьшения относительного содержания растворителя в исследуемых штрихах в течении определенного промежутка времени с момента начала анализа остаточных количеств растворителя в штрихах t. Время выполнения исследуемых штрихов Х рассчитываются по формуле
,
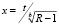где t – время старения штрихов с момента начала исследования;
,
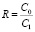C0 – относительное содержание растворителя в исследуемых штрихах на начало исследования,
C1 – относительное содержание растворителя в исследуемых штрихах через время t с момента начала исследования.
Хочется отметить, что в [1, 2] параметр (b) в контексте процесса не описан полно. Декларируется, что он определяется лишь как показатель степенной функции, который определяется эмпирически и/или оценивается путем сравнения характеристик относительного содержания растворителя в них с аналогичными характеристиками штрихов-моделей, давность выполнения которых совпадает с проверяемой датой в пределах допустимой погрешности, представленных в графическом или табличном виде. Протяженность временного интервала фактического времени выполнения исследуемых штрихов определяют по минимальному и максимальному значениям возраста штрихов-моделей, представленных в графическом или табличном виде и характеризующихся такими же значениями относительного содержания растворителя, что и исследуемые штрихи с учетом точности определения этих характеристик.
Это означает, что существует штрих-модель, которая подобрана как аналог исследуемого штриха по определенным критериям. При этом получается, что эту штрих-модель уже должны были исследовать в абсолютно тех же условиях, что и исследуемый (сравниваемый) штрих на предмет изменения величины концентрации растворителя в разные периоды времени, и по полученным данным математически описана зависимость изменения относительной концентрации растворителя от времени «жизни» объекта; вычислены коэффициент A и показатель степени b этой (степенной) зависимости в результате анализа полученных статистических данных.
Для получения динамической модели «старения» штриха, которая должна определятся изменением в уровне измеряемого параметра (в этом конкретном случае – концентрации растворителя) как функции времени, и вывода формулы зависимости времени от величины измеряемого параметра (формулы определения «возраста» исследуемых штрихов) необходимо уточнить, что степенная функция определяется как минимум тремя парами значений. А значит для начала необходимо получить такие пары значений (время / изменяемый параметр), как величина измеряемого параметра в условную единицу времени (сутки, неделя, месяц) и величина единиц времени, когда измеряемый параметр примет значение единица.
То есть в действительности, формулу расчета возраста исследуемых штрихов [1, 2] можно легко получить, если математически описанные зависимости, как например, представленные в [рис. 1 и 2] построить в обратных координатах и получить их формулы. Только в этом случае величина t, описанная как «время старения штрихов с момента начала исследования», будет представлять из себя величину единиц времени, когда измеряемый параметр примет значение единица.
Чтобы получить формулу предлагаемого вида, где величина t была бы равна известной из опыта конкретной величие времени, необходимо нормировать полученные величины значений измеряемого параметра от времени на величину измеряемого параметра в этот известный момент времени.
Хочется подчеркнуть, что t – не «промежуток времени между двумя исследованиями», а именно значение величины времени, при котором точно известна величина измеряемого параметра, по численной величине которого и проводится нормировка данных. Но в том и проблема, что единственна численная величина времени, известная при данном варианте исследования – это промежуток времени между двумя исследованиями. Т.е. получив значения C0 и C1 при расчетах согласно декларируемой методики РФЦСЭ, мы не можем знать, какому времени «жизни» они соответствуют. Из этого следует, что использовать формулу, приведенную в [1, 2] для датировки штрихов в том виде как она описана, невозможно практически.
В самом деле, если согласно [1, 2]
,
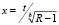где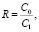 
то получим
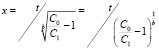
и далее
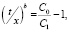
что очевидно не соответствует реальным расчетам, исходя из зависимости, приведенной в уравнении С = А∙xb. Иными словами, если взять величины концентраций C0 и Cх на любом промежутке времени t где:
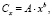
x – время старения штрихов с момента начала исследования, то всегда будет:
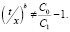
Или иначе:
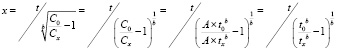
и далее
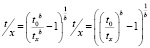
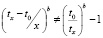
где t = tx – t0 время старения штрихов с момента начала исследования.
Таким образом, декларируемое авторами методики РФЦСЭ применение формулы для определения времени выполнения исследуемых штрихов с использованием отношения величин концентраций, полученных от исследуемого объекта в первый и второй день исследования, и с учетом численной величины промежутка времени между этими днями исследования – не имеет математического смысла.
Очевидно по этой причине в [1, 2] как дополнение к вышеописанной формуле, для определения возраста исследуемых штрихов авторами предлагается так же провести «моделирование процесса старения», которое заключается в оценке «путем сравнения характеристик относительного содержания растворителя в них с аналогичными характеристиками штрихов-моделей, давность выполнения которых совпадает с проверяемой датой в пределах допустимой погрешности, представленных в графическом или табличном виде, и протяженность временного интервала фактического времени выполнения исследуемых штрихов.
Т.е. величины концентрации растворителя, полученные через взятый промежуток времени от исследуемого объекта (единственные данные, которые можно получить от исследуемого объекта), следует экстраполировать на аналогичные данные штриха-модели. Причем, каким практическим способом это должно приходить не описано – просто сравнить и все. При этом какой-либо приемлемый критерий сравнения у авторов не приводится.
Однако, исходя из полученных данных очевидно, что единственно возможным, математически обоснованным критерием в данном случае является численная величина, которую можно обозначить, например, как kt, определяемая по формуле:
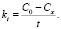
Примечание. В обозначении kt индекс t означает, что он определяется на конкретном временном промежутке численно равном t.
Данный критерий может быть описан как снижение численной величины концентрации растворителя за взятый промежуток времени или как скорость снижения концентрации растворителя на взятом промежутке времени (ед. концентрации в ед. времени).
Исходя из наличия получаемых данных, согласно [1, 2], для демонстрации способа и возможностей моделирования процесса старения штриха посредством «сравнения» данных, полученных от исследуемого объекта kt, с данными гипотетически возможных штрих-моделей, можно привести пример, в котором присутствуют:
– верно подобранная штрих-модель, математически представленная параметрами A1 и b1,
– неверно подобранные штрих-модели, математически представленные параметрами A2, b2 и A3, b3 соответственно.
Вычислим критерий kt для условно правильно подобранного варианта штрих-модели, когда «возраст» исследуемого штриха составлял бы 200 суток на первый день проведения исследования на промежутке времени между двумя исследованиями в 100 суток. С учетом париметров A1 и b1 он бы составил величину 0,12.
Но та же самая величина 0,12 в неверных вариантах выбора штрих модели определяла бы «возраст» исследуемого штриха на первый день исследования:
– в случае выбора штрих-модели с параметрами A2 и b2 – 300 суток,
– в случае выбора штрих-модели с параметрами A3 и b3 – 100 суток.
Вариант расчета по параметрам верно подобранной штрих-модели (A1 и b1) следующий:
– численная величина концентрации растворителя на первый день исследования C0 составляет 43,28;
– численная величина концентрации растворителя на второй день исследования C1 составляет 31,29;
– численная величина промежутке времени между двумя исследованиями t = 100 суток.
Таким образом, расчетная величина критерия kt составит:
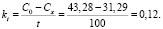
Данные проведения такого моделирования представлены в табл. 1.
Таблица 1
Сравнительная таблица результатов процесса «моделирования» путем сравнения характеристик различных штрихов-моделей и вычисленного критерия kt
|
T |
величина измеряемого параметра в условную единицу времени A |
||
|
верно подобранная штрих-модель |
неверно подобранная штрих-модель |
||
|
A1 |
A2 |
A3 |
|
|
3000 |
5500 |
5500 |
|
|
показателя степени уравнения вида y = Axb |
|||
|
b1 |
b2 |
b3 |
|
|
– 0,8 |
– 0,8 |
– 1,2 |
|
|
1 |
3000 |
5500 |
5500 |
|
10 |
475,5 |
871,7 |
347,0 |
|
100 |
75,4 |
138,2 |
21,9 |
|
200 |
43,28 |
79,3 |
9,5 |
|
300 |
31,29 |
57,4 |
5,9 |
|
400 |
24,9 |
45,6 |
4,1 |
|
X |
критерий сравнения kx вычисленный по данным полученным от исследуемого объекта за одинаковый промежуток времени |
||
|
100 |
0,12 |
||
|
200 |
0,12 |
||
|
300 |
0,12 |
||
где T – значение величины времени в который определяли величину концентрации растворителя согласно формулы С = А∙xb у штрихов-моделей; X – поучаемая давность нанесения штриха (на первый день проведения исследования) по результатам «моделирования»: промежуток времени между двумя этапами исследования 100 суток.
Выделяем два варианта сравнений с различными штрих-моделями:
1) в случае b1 равна b2;
2) в случае А2 равна А3.
В приведенной таблице приведены варианты, где во всех предлагаемых различных штрих-моделях для «сравнения» возможен вариант совпадения величины kt в различные временные периоды «жизни» штриха, при этом данные представленные в таблице вычислены с коэффициентом корреляции R2 = 1.
Как видно из полученных результатов, численная величина критерия сравнения kt пригодна только тогда, когда у выбранной штрих-модели точно определены параметры уравнения зависимости величины измеряемого параметра от времени нанесения исследуемого объекта A и b, и они получены от имеющих существенное сходство (по совокупности значимых параметров) исследуемому объекту и получены в аналогичных условиях. В противном случае ошибка в датировке может быть в разы больше или меньше реальной даты.
В частности, при одинаковом критерии kt = 0,12, используемая штрих-модель с давностью в 300 дней, с неверно подобранными или с неверно вычисленными параметрами A и b может привести к ошибкам расчётной давности нанесения штриха как в 200 дней, так и в 400 дней.
При этом каким-то иным способом «математического моделирования» либо иным сравнением хоть как-то приблизительно провести датировку исследуемого штриха математически невозможно.
С учетом всех перечисленных доводов, метод «математического моделирования», согласно декларируемой методики Минюста [1, 2] даже с использованием критерия kt не описанного авторами – не может быть применимым на практике.
Возможности описания процесса «старения» красящего вещества в штрихе во времени
Как уже описано выше изменение относительной концентрации растворителя в зависимости от времени описывают степенным уравнением:
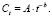(1)
Формула для определения времени, которое прошло с момента нанесения штриха (давности нанесения по отношению ко времени первого этапа исследования) по остаточной величине концентрации определяемого растворителя:
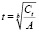
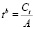
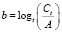
Поскольку функция Ct = f(t) – убывающая, график зависимости критерия b от t при A-const. будет иметь вид (рис. 1).
Рис. 1. Зависимость изменения интенсивности процесса b в зависимости от времени исследования t
Отсюда очевидно, что если bt = f(t), то соответственно величина критерия b будет характеристикой динамики процесса в зависимости от времени, описанного формулой (1), и тогда уместно будет записать:
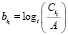
Промоделировав изменение величины значимого параметра Ct в зависимости от величины t, возможно представить динамику процесса «старения» уравнением (с использованием «условного математического критерия отношения» х*), как зависимость изменения интенсивности процесса b от времени, уравнением
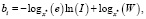(2)
где bi – интенсивность динамики процесса «старения» в определенный момент времени I;
W – значение величины времени, при котором точно известна величина измеряемого параметра;
x* – «критерий отношения» а именно, ордината общей точки логарифмических зависимостей вида:
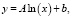
полученных по заданному алгоритму отношения величин цветового различия от контрольного и опытного штрихов за определенный промежуток времени. Если провести преобразование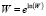 
и подставить преобразование в уравнение (2), получаем:
.
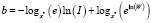
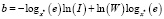
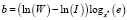Получим формулу описывающую изменение интенсивности процесса «старения» в зависимости от времени:
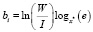. (3)
И, таким образом, легко заметить, что численная величина параметра интенсивности b будет зависеть от I и величины «параметра отношения» x*. Соответственно формула для определения времени давности нанесения исследуемого штриха с использованием параметра отношения x* будет иметь вид:
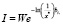. (4)
Данная математическая модель, описанная с использованием предлагаемого критерия, будет иметь несколько констант:
1. 
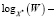величина b (в момент времени 1) 
,
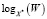2. 
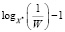– величина b (в момент времени A×W),
3. 
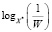– величина b (в момент времени W2),
4. 
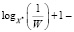величина b (в момент времени 1/X*),
5. 0 – величина b (в момент времени W).
Это численные величины, которые позволяют охарактеризовать концепцию оценки возраста штриха, как временных интервалов быстрой, умеренной и медленной интенсивности старения:
– быстрая интенсивность старения от момента времени 1 до момента времени W2;
– умеренная интенсивность старения от момента времени W2 до момента времени A×W;
– медленная интенсивность старения от момента времени A×W.
Хотелось бы отметить, что попытка представить и математически описать процесс «старения» материалов письма экспоненциальной зависимостью по полученным данным изменения относительного содержания растворителя в штрихах в зависимости от времени, уже предпринималась [6]. Согласно авторам, было проведено несколько серий экспериментов, направленных на изучение особенностей старения штрихов, выполненных гелевыми чернилами на бумаге для офисной техники.
Полученные результаты свидетельствуют о том, что изменения относительного содержания растворителя в штрихах в зависимости от времени, математически описывались экспоненциальной зависимостью с коэффициентом корреляции выше, чем у степенной функции.
Вопросы спектрального измерения и расчетов координат цвета и цветности
Рассмотрим основные вопросы, возникающие при спектральном измерении координат цвета и цветности (косвенная колориметрия). Согласно литературным данным этот метод является наиболее точным из всех известных методов, например, используя классический трехцветный колориметр мы не можем получить абсолютную погрешность менее, чем ± 0,05 [8] по координатам x и y. Это связано с тем, что спектральные характеристики каналов колориметра, практически невозможно реализовать в точности с кривыми сложения цветов МКО (особенно канала Χ, где кривая сложения имеет двугорбую кривую, рис. 2).
Для начала построим структурную схему, изображенную на рис. 3.
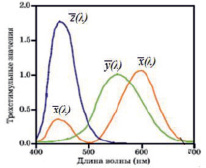
Рис. 2. Кривые сложения МКО 1931 г. (x, y)
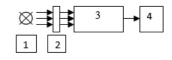
Рис. 3. Структурная схема измерения оптического спектра. 1 – источник света; 2 – исследуемый (измеряемый) объект; 3 – спектральный прибор (спектрофотометр); 4 – регистрирующая система
На этом рисунке, в качестве исследуемого объекта может быть прозрачная кювета с растворенным в растворителе штрихом. Таким образом, исследуемый объект можно рассматривать как обычный светофильтр, имеющий определенный спектр прозрачности, который «вырезается» из оптического спектра источника света. Отсюда следует, что источник света не может иметь какие-то спектральные линии излучения или поглощения. Оптический спектр излучения источника должен быть сплошным и достаточно гладким. На рис. 4 приведены спектры излучения стандартных источников.
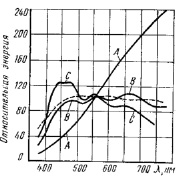
Рис. 4. Распределение энергии в спектре излучения стандартных источников белого света А, B, С и в дневном солнечном свете (штриховая линия) [9]
Как видно из этого рисунка, наиболее подходящим в качестве источника света является стандартный источник А (достаточно приближенно можно использовать обычную лампу накаливания).
Далее, после измерения ординат спектра, производится вычисление координат цвета по известным формулам:
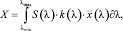
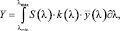(5)
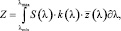
где λmin, λmax – границы оптического спектра, в нм;
S(λ) – ординаты измеренного спектра по длинам волн;
k(λ) – поправочный коэффициент, учитывающий реальную спектральную характеристику чувствительности фотоэлектрического тракта спектрального прибора;
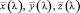– кривые сложения цветов.
Обычно, определенные интегралы вида (5) заменяются суммами:
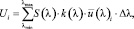(6)
где Ui – равно координатам цвета Х, Y и Ζ;
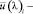равно кривым сложения 
;
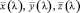i = 1, 2, 3 – порядковый номер уравнений (5);
∆λ – шаг дискретизации спектра по длинам волн.
Формула (6), называется в математике метод прямоугольников и позволяет вычислить площадь, ограниченную осью абсцисс (ось длин волн) и кривой измеренных ординат. Очевидно, что точность вычисления этой площади зависит от шага дискретизации измеряемого спектра, а также от самого вида этого спектра. И чем меньше значение Δλ, тем точнее будет вычислена сумма (6), т.е. значение по интегральной площади. Преследуя увеличение точности, можно вычислять значения интегралов по формуле трапеций.
Рассмотрим значение поправочного коэффициента k(λ). Очевидно, что сквозная спектральная характеристика фотоэлектрического тракта всей установки в зависимости от длины волны имеет различное значение. Поэтому без этого спектрального поправочного коэффициента измеренный спектр не будет истинным, а значит и вычисленные значения координат цвета при сколь угодным малым шаге дискретизации будут иметь ошибку, которая может иметь значительную величину. Для определения этого коэффициента можно сделать следующее. Измерить спектр стандартного источника А, который теоретически заменяет (моделирует) собой спектр абсолютно черного тела (АЧТ), разогретого до температуры 28540 К. Измерив ординаты источника A, найдем искомый коэффициент k(λ) по следующему отношению:
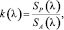
где Sp(λ) – рассчитанный спектр АЧТ при температуре 28540 К по формуле Планка;
SA(λ) – измеренный спектр источника А.
Необходимо отметить, что как источник А, так и источник света (рис. 4) должны питаться постоянным стабилизированным током.
И следующее, перед началом любых спектральных измерений, необходимо регистрирующее устройство установить в ноль, при этом на входную щель спектрального прибора не должен попадать свет.
Применение строго равноконтрастной системы координат при расчетах возраста штрихов
В начале 40 годов прошлого столетия Мак Адам опубликовал результаты экспериментов по определению порогов цветоразличения глазом человека [10]. Эти результаты были повторены Стайлсом [11] и Вышецки [12] и впоследствии вновь повторены Мак Адамом. Все результаты в достаточной степени согласуются между собой, приведены в колориметрической системе МКО 1931 г. (x, y) и хорошо известны специалистам. На диаграмме МКО 1931 г. (x, y) результаты выглядят как эллипсы, причем размеры и ориентация эллипсов зависит от значения цветности. Наличие эллипсов, а не кругов говорит о недостатках колориметрической системы МКО 1931 г. (x, y).
Впоследствии многие авторы разрабатывали так называемые равноконтрастные цветовые системы, к которым, к примеру, можно отнести: МКО 1960 г. (u, v), МКО 1976 г. (a*,b*) и другие. Но как, показали расчеты [12, стр. 294, таб. 7.2] ни одна существующая колориметрическая система не позволяет отразить на цветовой диаграмме вместо эллипсов Мак Адама – равновеликие окружности.
Поверхность цветового пространства любой системы можно характеризовать эллиптичностью поверхности [14], определяемую как:
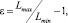
где Lmax – максимальная ось эллипса,
Lmin – минимальная ось эллипса.
В табл. 2 приведены значения эллиптичности поверхности цветового пространства некоторых систем. В этой же таблице приведены значения порога цветоразличения для стандартного наблюдателя МКО и максимальное отношение площадей эллипсов Мак Адама.
Из табл. 2 видно, что ни одна цветовая поверхность не имеет значения ε = 0, которое было бы идеально для поверхности цветового пространства.
Необходимо отметить, что Мак Адам проводил эксперименты по определению порогов цветоразличения при постоянной яркости излучения стимула. Поэтому, его результаты интерпретировались в двумерном цветовом пространстве, в частности на цветовом локусе МКО 1931 г. (x, y). Автором данной статьи был разработан программный комплекс по измерению порогов цветоразличения [12, 15, 16]. Впоследствии этот программный комплекс был изменен и дополнен с учетом зависимости порога цветоразличения от значения яркости стимула. Интерпретация результатов измерений может быть представлена, как это показано на рис. 5. Однополостный гиперболоид (рис. 5) сильно похож на результат решения уравнения Эйнштейна, описывающего состояния пространства-времени, решенное Шварцшильдом [17], приведенный на рис. 6.
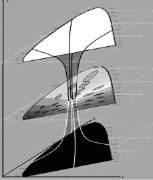
Рис. 5. Зависимость величины порогов цветоразличения от яркости стимула
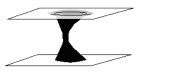
Рис. 6. Сечение пространства Шварцшильда при Т = 0
Рис. 6 Шварцшильд получил в результате решения уравнения гравитации (уравнение Эйнштейна).
Известно, что уравнение Эйнштейна имеет вид [18]:
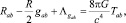(7)
где Rab – тензор кривизны Риччи, получающийся из тензора кривизны пространства-времени Rabcd посредством свёртки его по паре индексов, R – скалярная кривизна, то есть свёрнутый тензор Риччи, gab – метрический тензор, Λ – космологическая постоянная, Tab представляет собой тензор энергии-импульса материи, (π – число, с – скорость света в вакууме, G – гравитационная постоянная Ньютона). Так как все входящие в уравнения тензоры симметричны, то в четырёхмерном пространстве-времени эти уравнения равносильны скалярным уравнениям.
Таблица 2
Характеристики поверхности цветовых пространств
|
№ п/п |
Наименование цветовой системы |
Значение эллиптичности цветовой поверхности (ε) |
|
1 |
МКО 31(r, g, b) |
24,0 |
|
2 |
МКО 31 (х, у) |
25,9 |
|
3 |
МКО 60(u, v) |
2,2 |
|
4 |
МКО 76(u*, v*) |
13,9 |
|
5 |
МКО LAB |
15,4 |
|
6 |
Система YIQ |
25,5 |
|
7 |
Система CMY |
24,0 |
|
8 |
Система (α, β) [13] |
0,2 |
Уравнения А. Эйнштейна не налагают никаких ограничений на используемые для описания пространства-времени координаты, т.е. обладают свойством общей ковариантности, но они ограничивают выбор лишь 6 из 10 независимых компонент симметричного метрического тензора. Поэтому их решение неоднозначно без введения некоторых ограничений на компоненты метрики, соответствующих однозначному заданию координат в рассматриваемой области пространства-времени, и обычно называемых координатными условиями.
Как видно в уравнении (7), в правой части используются такие физические константы, как гравитационная постоянная Ньютона G, скорость света с, и тензор энергии-яркости Lab, значения, компоненты которого определяются из соотношений яркости в различных точках полученной сферы. Космологическая постоянная Λ (для нашего случая цветового пространства) равна нулю, тогда уравнение (7) примет следующий вид:
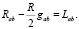(8)
Введем понятие цветовой тензор.
Любой точке на цветовом локусе можно сопоставить некий цветовой вектор. Для начала, свяжем такие понятия, как цветовая насыщенность и цветовой тон с системой координат МКО 1931 (x, y). Для чего сделаем параллельный перенос осей x, y так, чтобы начало координат совпадало с координатами «белого» цвета. Очевидно, для системы МКО 1931 (x, y) это будет цветность равно энергетического источника E с координатами xE = 0,3333 и yE = 0,3333. Тогда цветовой локус будет иметь вид, как это изображено на рис. 7.
Рис. 7. Пороги Мак Адама в системе координат x’ y’
Рис. 8. Сечение эллипсоидов плоскостью x’0L (левая часть рисунка) и их преобразование в равновеликие шары (сечение той же плоскостью правая часть рисунка). Размер эллипсоидов и шаров эллипсов и сфер приведены в соответствии [12]
Рис. 9. Сечение эллипсоидов плоскостью y’0L (левая часть рисунка) и их преобразование в равновеликие шары (сечение той же плоскостью правая часть рисунка). Размер эллипсоидов и шаров увеличен в 10 раз. Номера эллипсов и сфер приведены в соответствии [12]
На рис. 7 длина вектора 0S отображает цветовую насыщенность центра эллипса Мак Адама, а угол φ – цветовой тон.
Поскольку все вектора типа 0S (рис. 7) начинаются из нулевой точки, то длина этих векторов (цветовая насыщенность) определяется простым выражением типа:
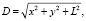
где x, y – координаты конца вектора в системе координат x’ y’; L – яркость точки конца вектора.
Согласно закону Бугера-Фехнера, порог по яркости равен 0,01 от текущей яркости.
Цветовой вектор может быть представлен следующей матрицей:
. (9)
Разложив вектор (9) по ортам базиса e1, e2, e3, получим двухвалентный симметричный цветовой тензор Cab. Суть этого тензора заключается в задании координат для метрического тензора в (8) конкретной точке на цветовой диаграмме. Здесь мы будем рассматривать систему МКО 1931 г. (x, y), причем, с переносом начала координат, как это было сказано выше. Пожалуй, что в качестве цветовой диаграммы здесь можно использовать любую из известных систем МКО.
Не будем утруждать читателя достаточно сложными математическими преобразованиями, а приведем конечный результат.
Сам цветовой локус оставляем без изменения, а эллипсоиды отображаем в новой сферической системе координат, что дает трансформацию их в сферы одинаковых радиусов.
На основе приведенного математического аппарата и, учитывая, что уравнения эллипсоида вращения согласно [13] имеет вид:
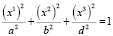
где a, b, d – длина полуосей эллипсоида,
а уравнение сферы, согласно [14], имеет вид:
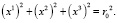
Здесь предполагается, что центры, как эллипсоида, так и сферы совпадают с началом координат, а координаты x1, x2, x3 – соответствуют привычным x, y, z. На рис. 8 и 9 представлены результаты расчетов (трансформации эллипсоидов в шары одинакового диаметра). На этих рисунках показано только пять эллипсоидов, с целью не загромождения этих рисунков. С этой же целью на рисунках показаны сечения эллипсоидов плоскостями X0L и Y0L.
В качестве примера, здесь показано преобразование цветового пространства МКО 1931 г. (x, y), но в данное строго равноконтрастное цветовое пространство можно преобразовать любую известную цветовую систему. При этом результат преобразования получится в представлении геометрии Риммана с подвижными координатами, т.е. полученная система становится динамической. Такую систему можно представить следующим образом:
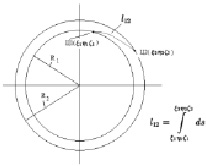
Рис.10. Определение цветового различия двух цветов Ц1 и Ц2, имеющих отличные яркости и находящиеся на разных сферических поверхностях, радиус которых однозначно определяется яркостью цвета
В заключение приведем функциональную зависимость, полученную на основе строго равноконтрастной цветовой системы, построенной автором на основе колориметрической системы LAB (МКО 1976 г.) и величин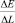 
от времени (рис. 11). Необходимо отметить, что погрешность отклонения от линейности изображённой прямой, построенной по трем точкам, от прямой, построенной по первым двум точкам, составляет не более 0,5 %, что можно списать на погрешность измерения.
Рис. 11. Динамическое изменение отношения 
Так же укажем, что автором был получен патент на изобретение на разработку строго равноконтрастного цветового пространства (световой системы) [18].
Заключение
Динамика изменения отношений цветовых координат красящего вещества в штрихе моделируется по тем же математическим принципам, по которым возможно смоделировать и процесс изменения концентрации растворителя в штрихе от времени.
В данной статье разработаны критерии построения динамической модели процесса старения, описаны возможности и принципы проведения измерений, а также определения выбранной зависимости такого процесса.
Объяснены основные принципы спектральных измерений окрашенных растворов и проведения расчетов на основании полученных данных координат цвета и цветности.
Показаны возможности применения строго равноконтрастной цветовой модели для получения выбранного параметра, который бы определял интенсивность процесса изменения параметров цвета, как абстрактную математическую величину, которая может характеризовать возраст штриха реквизита документа.
Библиографическая ссылка
Ложкин Л.Д., Ситников Б.В., Веневцев А.Н. К ВОПРОСУ О МОДЕЛИРОВАНИИ ПРОЦЕССОВ СТАРЕНИЯ ШТРИХОВ РЕКВИЗИТОВ ДОКУМЕНТОВ С ЦЕЛЬЮ УСТАНОВЛЕНИЯ АБСОЛЮТНОЙ ДАВНОСТИ ИХ ВЫПОЛНЕНИЯ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 8-2. – С. 213-226;URL: https://applied-research.ru/ru/article/view?id=7071 (дата обращения: 21.11.2024).