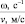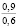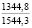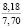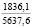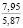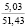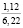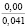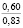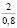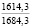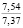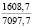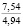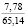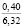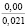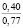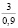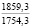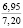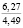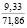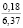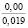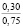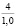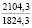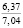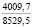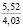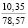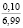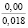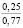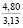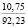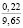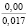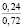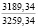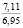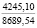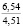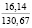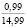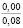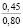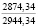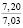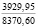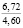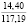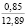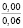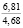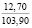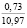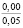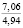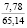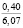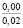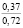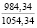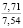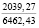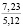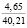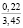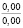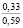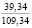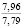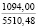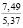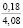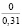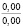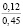Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Золотаревская Д.И. 1

---

1 Российский государственный аграрный университет – МСХА им. К.А. Тимирязева

Исследованы процессы релаксации напряжений в уплотняющихся связных почвах, происходящие после их кратковременного начального деформирования по гармоническому, а также по линейному законам. Вязкоупругие свойства уплотняющихся почв описаны дифференциальным уравнением первого порядка, связывающим сжимающие напряжения, скорости изменения сжимающих напряжений и относительной деформации сжатия. Рассмотрены вязкоупругие свойства дерново-подзолистой легкосуглинистой почвы, выявленные в полевых испытаниях. В исследовании учтено, что плотность почвы переменна по глубине деформируемого слоя. На основании статистической обработки экспериментальных данных зависимость начальной плотности почвы от глубины принята квадратичной. Выполнены компьютерные эксперименты, в которых найдены показатели, позволяющие оценить количественно изменения деформаций, напряжений в почве и плотности почвы при ее начальном деформировании. В компьютерных экспериментах найдены также показатели, характеризующие релаксационные процессы в почве, происходящие после ее начального динамического деформирования. Выявлено влияние на эти показатели начальной плотности почвы, ее влажности, скорости деформирования и других факторов.

Статья в формате PDF

1450 KB

вязкоупругие свойства почв

деформации

сжимающие напряжения

уплотнение почвы

релаксация напряжений

математическое моделирование

1. Бондарев А.Г., Медведев В.В., Русанов В.А. Уплотнение почв техникой // Проблемы почвоведения. Советские почвоведы к XIV Международному конгрессу почвоведов. Сб. научных трудов. – М.: Наука, 1990. – С. 20–25.

2. Вялов В.В. Реологические основы механики грунтов. – М.: Высшая школа, 1978. – 447 с.

3. Денисов Н.Я. О природе деформаций глинистых пород. – М.: Изд-во министерства речного флота, 1951. – 200 с.

4. Золотаревская Д.И., Бурдыкин В.И., Матвеев В.В. и др. Изменение вязкоупругих свойств почвы при воздействии колесного трактора // Известия ТСХА – 1987. – Вып. 3. – С. 173–180.

5. Золотаревская Д.И. Закономерности деформирования почв: Математическое моделирование. – М.: «Книжный дом Либроком», 2013. – 144 с.

6. Золотаревская Д.И., Иванцова Н.Н, Лядин В.П. Математическое моделирование деформирования почв при качении колес // Тракторы и сельскохозяйственные машины. – 2008. – № 5. – С. 28–33.

7. Золотаревская Д.И. Математическое моделирование релаксационных процессов в почвах // Почвоведение. – 2003. – № 4. – С. 429–440.

8. Золотаревская Д.И. Основы теории и методы расчета уплотняющего воздействия на почву колесных движителей мобильной сельскохозяйственной техники: Автореф. дис... докт. техн. наук. – М., 1997. – 49 с.

9. Золотаревская Д.И. Особенности качения колес по вязкоупругой почве // Тракторы и сельскохозяйственные машины. – 2005. – № 8. – С. 22–27.

10. Колтунов М.А., Кравчук А.С., Майборода В.П. Прикладная механика деформируемого твердого тела. – М.: Высшая школа, 1983. – 352 с.

11. Манучаров А.С., Абрукова В.В., Черноморченко Н.И. Методы и основы реологии в почвоведении. – М.: Изд-во МГУ, 1990. – 98 с.

12. Ксеневич И.П., Скотников В.А., Ляско М.И. Ходовая система – почва – урожай. – М.: Агропромиздат, 1985. – 304 с.

Проблема сохранения и повышения плодородия почв является в настоящее время одной из наиболее актуальных экологических проблем; ее решению посвящены исследования широкого круга ученых. Природные условия и антропогенные воздействия на почву оказывают существенное влияние на ее свойства. Предпосевное прикатывание почвы почвообрабатывающими катками способствует оптимизации ее свойств, а многократные проходы по полю тракторов и другой мобильной сельскохозяйственной техники приводят к переуплотнению почвы. Переуплотнение почв в результате воздействия ходовых систем мобильных машин вызывает ухудшение агротехнических свойств почв, снижение их плодородия и урожайности сельскохозяйственных культур [12].

Для получения высоких и устойчивых урожаев необходимы благоприятные физические свойства почв. Основными параметрами, определяющими эти свойства, являются гранулометрический состав почв и содержание в них органических веществ, а также плотность и влажность почвы [1]. Большое влияние на свойства почв, от которых зависит урожайность сельскохозяйственных культур, оказывают сжимающие напряжения σ, возникающие в почвах в результате воздействия ходовых систем мобильных машин.

Для решения практических задач важно находить зависимости между внешними нагрузками и соответствующими им деформациями почв с учетом фактора времени, то есть с учетом реологических свойств почв. Математическое моделирование процессов деформирования почв, основанное на результатах исследований их реологических свойств, позволит разработать эффективные меры защиты почв от вредных воздействий сельхозтехники.

При влажностях w почвы, меньших ее полной влагоемкости, и при сжимающих напряжениях σ, меньших предела ее прочности σ_пр, почва под действием нагрузки уплотняется и упрочняется. Неуплотненные почвы при таких w являются вязкоупругими [3, 5]. Время t взаимодействия с почвой движителей мобильных машин и рабочих органов сельскохозяйственных машин и орудий при выполнении полевых работ весьма мало. Поэтому важно исследовать изменение вязкоупругих свойств и плотности почв при таких малых значениях t.

Ранее нами в работе [7] был предложен метод расчета, позволяющий находить показатели напряженно-деформированного состояния почвы в различных условиях нагружения и приращение плотности почвы на различной глубине, возникающее в результате действия внешней нагрузки; исследован процесс релаксации напряжений в почве.

Цели данной работы состояли в следующем: развить полученные в работе [7] результаты исследования и математического моделирования деформирования и уплотнения почвы с учетом ее вязкоупругих свойств; уточнить и применить предложенный метод расчета показателей напряженно-деформированного состояния и уплотнения почвы, изменяющихся при кратковременном динамическом деформировании, а также расчета показателей последующего процесса релаксации напряжений в почве.

Материалы и методы исследования

Нами проведены теоретическое исследование изменения характеристик вязкоупругих свойств уплотняющейся связной почвы, показателей ее напряженно-деформированного состояния и уплотнения при кратковременном динамическом деформировании по гармоническому, а также по линейному законам, теоретическое исследование релаксации напряжений в почве после кратковременного динамического деформирования почвы. На основе использования полученных нами экспериментальных данных выполнены компьютерные эксперименты по разработанным программам.

Результаты исследований и их обсуждение

Результаты экспериментального исследования вязкоупругих свойств почвы

На поле опытного хозяйства РГАУ – МСХА им. К.А. Тимирязева были проведены экспериментальные исследования вязкоупругих свойств, закономерностей деформирования и уплотнения почвы в результате действия динамических нагрузок при работе колесного трактора МТЗ-82 [4, 8]. Проведен ряд серий опытов, каждая из которых состояла из шести последовательных проходов по почве этого трактора. В данной работе использованы экспериментальные данные, полученные в работе [8]. Исследуемая почва – дерново-подзолистая легкосуглинистая. На экспериментальном поле верхний деформируемый слой почвы, распространенный на глубину H = 1,0 м, расположен на практически недеформируемом основании. Поверхность почвы горизонтальна.

Введем ось Oy, направленную вертикально вниз, начало которой O расположим на поверхности почвы. Плотность верхнего деформируемого слоя почвы перед проходами по ней машин (начальная) переменна по глубине y.

В работе [7] проведено исследование для почвы, верхний деформируемый слой которой до воздействия на нее штамповой нагрузки распространен на глубину H = 0,51 м. Зависимость плотности ρ этого слоя почвы от глубины y до воздействия на почву внешней нагрузки на основании результатов обработки экспериментальных данных была принята линейной.

В опытах, описанных в работе [8], на ряде участков поля, отобранных случайным образом, находили плотность ρ и влажность w почвы перед каждой серией опытов в слоях 0–0,1, ...., 0,9–1,0 м. Для получения аналитической зависимости ρ(y) в качестве представителя каждого слоя почвы принимали его середину. На сновании результатов статистической обработки экспериментальных данных в работе [8] зависимость плотности ρ верхнего деформируемого слоя почвы, распространенного на глубину H, до ее уплотнения колесами машин от глубины y приняли состоящей из двух линейных участков. При такой кусочно-линейной зависимости ρ(y) решение задачи об уплотнении почвы является весьма трудоемким. В результате статистической обработки экспериментальных данных из работы [8] нами были получены квадратичные зависимости плотности ρ от глубины y, которые с большой точностью заменяют найденные ранее кусочно-линейные зависимости. Получили

,

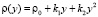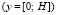, (1)

где k₁ и k₂ ≠ 0 – коэффициенты, ρ₀ – свободный член. Для почвы опытного поля (при w = 15,5 %, ρ₀ = 1,1412 г/см³, k₁ = 1,8762 г/(см³ м), k₂ = – 1,1374 г/(см³ м²); корреляционное отношение для зависимости (1) равно 0,9861. Высокое корреляционное отношение свидетельствует о весьма большой точности определения плотности почвы по формуле (1). При y∈[0;H] почву можно уплотнить, так как ρ(y) < ρ_пр, ρ(H) < ρ_пр, где ρ_пр – плотность предельно уплотненной почвы при σ < σ_пр.

В данной работе, в отличие от работ [7, 8], зависимость начальной плотности почвы от глубины y, описана уравнением (1).

На основании результатов исследований [4, 6, 8] закономерность сжатия почвы в направлении оси Oy при каждом фиксированном y будем моделировать дифференциальным уравнением

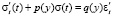, (2)

где σ – сжимающие напряжения, МПа; ε – относительная деформация сжатия; t – время, с.; p(y) и q(y), с^-1 и МПа – характеристики реологических (вязкоупругих) свойств почвы. Границы применимости этого уравнения для конкретных почв выявляют по экспериментальным данным. Адекватность уравнения (2) при моделировании закономерности сжатия легкосуглинистой почвы известного гранулометрического состава при w = 16–26 % и при определенных значениях t, σ, e, а также супесчаной почвы подтверждена экспериментально [4, 6, 8].

Характеристика p, с^-1 зависит от частоты w, с-1 гармонического процесса деформирования, возникающего, в частности, в результате деформирования почвы при качении цилиндрического штампа или колеса. В расчетных формулах, полученных на основе определяющего уравнения (2), ее целесообразно представить в виде p = wg, где g – преобразованная безразмерная характеристика вязкоупругих свойств почвы.

Путем статистической обработки большого числа экспериментальных значений g и q, полученных на опытном поле при различных ρ, w и w, найдены уравнения регрессии для определения при каждом фиксированном y характеристик g и q исследованной почвы:

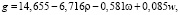(3)

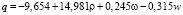(4)

с коэффициентами множественной корреляции, равными соответственно 0,7931 и 0,7528. Теснота связей в этих уравнениях достаточно большая, поэтому они могут быть применены в расчетах для исследованной почвы и для других почв, имеющих близкие к ней физические свойства. Уравнения (3) и (4) соответствуют следующим интервалам значений влияющих факторов: ρ = 1,14 – 1,88 г/см³, w = 15 – 26 %, w = 0,93 – 5,01 с^-1. В уравнениях (3) и (4) при y = 0 плотность почвы ρ = ρ₀.

Результаты теоретического исследования релаксации напряжений в почве после ее начального динамического деформирования и уплотнения

Пусть на поверхность почвы посредством штампа передается внешняя нагрузка. Ширина штампа принята достаточно большой, в этом случае деформацию почвы можно считать плоской. На основе математического моделирования процесса распространения в почве при ее нагружении вязкоупругих затухающих волн деформации сжатия почвы дифференциальным уравнением с частными производными четвертого порядка и с переменными коэффициентами были получены формулы, позволяющие найти глубину Hp распространения деформации сжатия почвы, приращение плотности и плотность почвы на различной глубине. Выполненные нами исследования показали, что при H ≤ 1 м глубина H_p = H. Относительная деформация сжатия почвы в каждый момент времени t равна

,

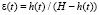где h(t) – переменная абсолютная деформация сжатия (осадка) почвы.

В теории вязкоупругости чаще рассматривают релаксационные процессы в деформируемых средах при постоянных уровнях напряжений или деформаций, создаваемых в результате ступенчатого статического изменения нагрузок, то есть принимают, что каждый определенный уровень напряжений или деформаций достигается мгновенно [10]. В данной работе, как и в других наших работах учтено, что внешняя нагрузка, действующая на почву, прикладывается к почве не мгновенно, а возрастает в течение некоторого отрезка времени.

В ряде работ, посвященных исследованию реологических свойств почв, рассмотрены релаксационные процессы, происходящие в течение нескольких минут [11]. Однако время взаимодействия с почвой движителей работающей на полях сельскохозяйственной техники составляет десятые или даже сотые доли секунды. В связи с этим нами исследована релаксация напряжений в почвах после начального деформирования в такие малые отрезки времени.

Процесс изменения во времени напряжений в материале или деформируемой среде при постоянной деформации называют релаксацией. С целью исследования процесса релаксации нами рассмотрено две стадии изменения напряженно-деформированного состояния почвы. Первая стадия соответствует времени t∈[0;t₀]. На этой начальной стадии изменяются деформации почвы и напряжения в ней: e = e(t), σ = σ(t). При t∈[0;t₀] e и σ возрастают: e∈[0;e₀], σ∈[0;σ₀].

Вторая стадия изменения напряженно-деформированного состояния почвы (стадия релаксации) соответствует t∈(t₀;∞). На этой стадии e = e₀ = const, а сжимающие напряжения с течением времени изменяются: σ = σ(t).

Нами проведено исследование процессов релаксации напряжений в почве после ее начального деформирования по гармоническому, а также по линейному (равномерное увеличение деформации) законам.

Пусть начальное деформирование почвы осуществляется по гармоническому закону :

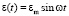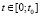, , (5)

где e_m – амплитуда деформации, w – угловая скорость деформирования. Подставим выражение 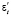скорости изменения относительной деформации сжатия почвы в определяющее уравнение (2). Учитывая начальное условие: при t = 0 напряжение σ = 0, найдем:

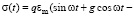
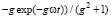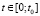, . (6)

Численные значения характеристик g и q вязкоупругих свойств почвы, входящие в формулу (6), соответствуют значению ρ = ρ₀.

В результате действия внешней нагрузки с течением времени t изменяются деформация почвы, глубина распространения деформации сжатия почвы, характеристики g и q ее вязкоупругих свойств. Осадка почвы и глубина распространения ее деформируемого слоя перед началом стадии релаксации соответственно равны: h₀ = h(t₀) Hн = H – h₀.

Получили формулу для определения приращения плотности почвы на различной глубине. При H_p = H и квадратичной зависимости (1) начальной плотности почвы от глубины приращение плотности почвы на глубине h₀ ≤ H приближенно равно

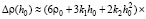
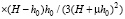, (7)

где μ – коэффициент поперечного расширения почвы. Приняли, что на глубине H почва до действия на нее внешней нагрузки имела максимально возможную плотность, поэтому ∆ρ(H) = 0.

На стадии релаксации за новое начало отсчета глубины – величины yн (то есть за новую поверхность почвы) принимаем координату y = h₀. Плотность почвы при y_н = 0 в начале процесса релаксации равна

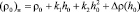. (8)

Зная приращение плотности почвы на различной глубине, найдем новые значения ее плотности ρ_н(y_н) для всех y_н∈[0,H_н]. Для H_1н – нового значения глубины, соответствующей глубине Н₁, новая плотность почвы равна ρ_н(H_1н).

В соответствии с полученными ранее результатами [5, 9] зависимость плотности почвы от глубины y_н аппроксимирована квадратичной функцией вида (1), но с измененными входящими в нее параметрами.

При изменении плотности почвы изменяются ее релаксационные свойства. Эти свойства определяются новыми значениями характеристик g₁ и q₁ ее вязкоупругих свойств. Характеристики g₁ и q₁ вязкоупругих свойств почвы на стадии релаксации соответствуют значению ρ = (ρ₀)_н.

На стадии релаксации e = e₀ = = e_m sin wt₀ = const. Учитывая, что в этом случае 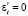и начальное условие: при 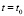напряжение 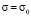, из уравнения (2) получим формулу, характеризующую процесс релаксации:

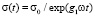, t∈(t₀;∞). (9)

Напряжение σ₀, входящее в формулу (9), вычисляем по формуле (6) при 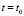. Из формулы (9) следует, что если 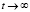, то напряжение .

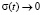Пусть начальное деформирование почвы осуществляется посредством плоского штампа по линейному закону

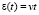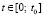, , (10)

где v > 0 = const – линейная скорость деформирования. Подставим выражение скорости изменения относительной деформации сжатия почвы в определяющее уравнение (2). Учитывая начальное условие: при t = 0 напряжение σ = 0, найдем:

,

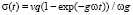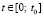. (11)

Характеристики g и q, а также g₁ и q₁ вязкоупругих свойств почвы и показатели ее уплотнения находим аналогично тому, как это сделано для случая начального деформирования почвы по закону (5).

На стадии релаксации e = e₀ = vt₀ = const. Учитывая, что в этом случае 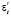 = 0, а также начальное условие: при t = t0 напряжение σ = σ₀, из уравнения (2) получим, что напряжения σ(t) характеризуются формулой (9). В эту формулу подставим значение

.

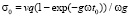Метод расчета изменения показателей напряженно-деформированного состояния почвы в результате кратковременного начального деформирования и релаксации

На основе выполненного математического моделирования нами разработан метод расчета изменения показателей напряженно-деформированного состояния почвы в результате кратковременного начального динамического деформирования и релаксации напряжений при зависимости (1) начальной плотности почвы от глубины в случае изменения начальной деформации e(t) по законам (5) и (10). Предложен также метод расчета показателей уплотнения почвы при ее начальном динамическом деформировании по этим законам. Исходными для выполнения каждого расчета являются следующие данные: Н, глубина 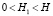, , 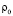, , 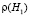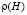w, e_m, t₀, коэффициенты уравнений регрессии 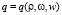, 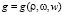(для исследовавшейся легкосуглинистой почвы это коэффициенты уравнений (3) и (4)), w (при начальном деформировании по гармоническому закону (5)) или v (при начальном деформировании по линейному закону (10)).

Характерные особенности предложенного метода расчета состоят в следующем. Величины деформации сжатия почвы, характеристик g и q ее вязкоупругих свойств, показатели напряженно-деформированного состояния и уплотнения почвы при деформировании почвы являются непрерывными функциями t. Приближенно считаем, что в малые промежутки времени эти величины постоянны и их изменение происходит дискретно.

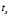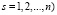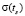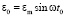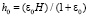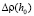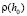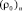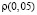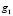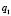Рассмотрим малые значения времени (. На первой стадии изменения напряженно-деформированного состояния почвы при t∈[0;t₀] находим при деформировании по гармоническому закону (5) напряжение по формуле (6), , , по формуле (7), . , – плотность почвы в слое 0 – 0,1 м, характеристики и вязкоупругих свойств почвы при 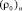. На второй стадии изменения напряженно-деформированного состояния почвы (стадии релаксации) приближенно считаем, что сжимающие напряжения постоянны в малые промежутки времени 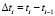. В расчетах приняли 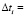0,02 с. Рассматриваем моменты времени 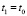, , 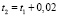, , 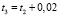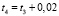..., 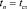, где t_ст – время стабилизации напряжений. По формуле (9) находим 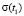, , 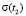, ,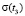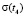..., . 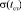В качестве приближенных значений tст принимали моменты времени, которым соответствуют значения  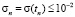кПа.

Аналогично выполняются расчеты при линейном законе начального деформирования почвы и последующей релаксации напряжений.

Результаты компьютерных экспериментов.

Анализ полученных результатов

Нами разработаны компьютерные программы, позволяющие найти по полученным формулам и алгоритмам показатели, характеризующие напряженно-деформированное состояние и уплотнение почвы в различные фиксированные моменты времени при начальном деформировании почвы и в процессе ее релаксации. По этим программам выполнены компьютерные эксперименты, в которых найдены указанные показатели для дерново-подзолистой легкосуглинистой почвы, вязкоупругие свойства которой исследованы опытах, описанных в работе [8]. Эти свойства, которые отражены также в данной работе, описывают уравнения (1)–(4). Характеристики вязкоупругих свойств почвы перед началом ее деформирования находили по уравнениям регрессии (3) и (4). Опыты по исследованию релаксации выполнили для двух режимов начального деформирования почвы при t∈[0;t0]: а) по гармоническому закону (5) (опыты группы А); б) по линейному закону (10) (опыты группы Б).

В случае начального деформирования почвы по гармоническому закону (5) исследовали влияние на релаксацию напряжений и уплотнение почвы: 1) ее начальной плотности, 2) угловой скорости деформирования (угловой частоты) w, 3) влажности w почвы, 4) времени t0 начального деформирования почвы, 5) амплитуды деформации em. Для выявления характера и количественной оценки влияния этих факторов выполнили базовый расчет и пять серий однофакторных компьютерных экспериментов (серии 1, А – 5, А). Базовый расчет провели по следующим исходным данным: H1 = 0,3 м; H = 1 м; ρ0 = 1,14 г/см3; 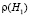= 1,7 г/см3; 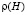= 1,88 г/см3; w = 20 %; t0 = 0,2 с; em = 0,04; w = 2 с-1. В каждой из пяти серий компьютерных экспериментов варьировали по одному из основных влияющих факторов, а остальные факторы принимали такими же, как в базовом расчете.

В случае начального деформирования почвы по линейному закону (10) исследовали влияние на релаксацию напряжений и уплотнение почвы: 1) ее начальной плотности, 2) скорости начального деформирования v, 3) влажности w почвы, 4) времени t₀. начального деформирования почвы, 5) амплитуды деформации e_m. Для выявления характера и количественной оценки влияния этих факторов выполнили базовый расчет и четыре серии однофакторных компьютерных экспериментов (серии 1, Б – 4, Б. Базовый расчет провели по следующим исходным данным: H₁ = 0,3 м; H = 1 м; ρ₀ = 1,14 г/см³; 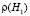= 1,7 г/см³; 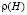= = 1,88 г/см³; w = 20 %; t₀ = 0,1 с; v = 0,8 м/с. В каждой из четырех серий компьютерных экспериментов варьировали по одному из основных влияющих факторов, а остальные факторы принимали такими же, как в базовом расчете.

В опытах серий 1, А и 1, Б выявили влияние начальной плотности почвы на исследуемые показатели. Каждая из этих серий состояла из пяти опытов. Начальную плотность почвы в каждом из опытов этих серий принимали по данным табл. 1.

Таблица 1

Начальная плотность почвы в ряде опытов

Опыты выявили значительное влияние начальной плотности почвы на изменение напряжений σ₀, деформаций e_(t) почвы, приращения плотности почвы и величины плотности почвы в различных ее слоях на стадии начального деформирования, релаксацию напряжений на стадии их релаксации, время t_ст стабилизации деформаций. В табл. 2 приведены данные, отражающие результаты опытов серии 1, Б. В этой таблице даны численные значения: ρ₀, k₁, k₂; напряжений σ₀, приращения плотности ∆ρ(0,05) и плотности ρ(0,05) почвы в слое 0–0,1 м при t = t₀; напряжений σ(t) в почве при их релаксации: σ(0,11) при t = 0,11 с и σ(0,6) при t = 0,6 с; времени t_ст при различных значениях начальной плотности почвы.

Таблица 2

Показатели уплотнения почвы, величины напряжений сжатия σ0 и их релаксация при различных значениях начальной плотности дерново-подзолистой легкосуглинистой почвы (в случае начального деформирования по линейному закону (10))

На рис. 1 представлены графики, отражающие изменение сжимающих напряжений в почве при ее начальном деформировании по гармоническому закону (5) и их релаксацию при различных значениях начальной плотности почвы.

Нами также получены кривые, характеризующие зависимости σ(t) для случая изменения e(t) при t∈[0;t₀] по закону (10). Построенные графики характеризуют процессы нарастания напряжений при t∈[0;t₀] и их релаксации при 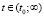. Представленные на рис. 1 кривые σ(t), а также другие, полученные расчетным путем данные показывают, что при равных e₀ в более плотной почве напряжения σ(t) больше, релаксируют и стремятся к нулю медленнее, чем в менее плотной; время tст с ростом плотности почвы возрастает.

В табл. 3 приведены данные, отражающие результаты серий опытов 2, А и 2, Б при различных значениях скорости начального деформирования. В этой таблице даны численные значения: характеристик вязкоупругих свойств почвы q₀ и g₀, а также q₁ и g₁, напряжений σ₀, приращения плотности ∆ρ(0,05) и плотности ρ(0,05) почвы в слое 0–0,1 м при t = t₀; напряжений σ(t) в почве при их релаксации: σ(0,21) при t = 0,21 с и σ(0,71) при t = 0,71 с; времени t_ст при различных значениях скорости начального деформирования.

Таблица 3

Характеристики вязкоупругих свойств почвы и релаксация напряжений в почве при различных значениях скорости ее начального деформирования

Примечание. Над чертой – при начальном деформировании по гармоническому закону (5), под чертой – по линейному закону (10).

На рис. 2 даны графики, отражающие изменение сжимающих напряжений в почве при ее начальном деформировании по гармоническому закону (5) и их релаксацию при различных значениях угловой скорости w ее начального деформирования. Нами также получены кривые, характеризующие зависимости σ(t) для случая изменения e(t) при t∈[0;t₀] по закону (10). Приведенные на рис. 2 зависимости σ(t), а также другие полученные в результате расчетов данные свидетельствуют о том, что большим значениям скорости начального деформирования соответствуют большие значения e₀, σ₀ и меньшее время релаксации напряжений в почве. При увеличении скорости начального деформирования в период времени t∈[0;t₀] уплотнение почвы также возрастает. Приращение ∆ρ(h₀) плотности почвы, наблюдающееся при t = t₀ с ростом w от 0,9 до 7,8 с^-1 увеличивается от 0,0162 до 0,0887 г/см³ (в 5,47 раза при ρ₀ = 1,14, ρ(0,3) =1,7, t₀ = 0,2 с).

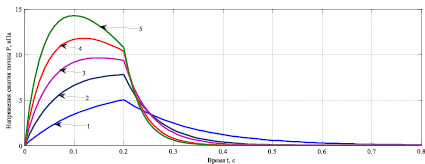
Рис. 2. Изменение во времени напряжений сжатия дерново-подзолистой легкосуглинистой почвы при ее начальном деформировании по гармоническому закону и их релаксация при различных значениях угловой скорости начального деформирования (влажность почвы w = 20 %, ε_m = 0,04, t₀ = 0,2 с, ρ₀ = 1,14 г/см³); 1, 2, 3, 4 и 5 – угловая скорость ω = 0,9; 2; 3; 4 и 5 с^-1).

Таблица 4

Характеристики вязкоупругих свойств почвы и релаксация напряжений в почве при различных значениях ее влажности

Примечание. Над чертой – при начальном деформировании по гармоническому закону (5), под чертой – по линейному закону (10).

Изменение влажности почвы вызывает изменение ее релаксационных свойств. В табл. 4 приведены данные, отражающие результаты серий опытов 3, А и 3, Б при различных значениях влажности почвы. В этой таблице даны численные значения: характеристик вязкоупругих свойств почвы q₀ и g₀, а также q₁ и g₁; напряжений σ₀; приращения плотности ∆ρ(0,05) и плотности ρ(0,05) почвы в слое 0–0,1 м при t = t₀; напряжений σ(t) в почве при их релаксации: σ(0,21) и σ(0,71); времени t_ст при различных значениях w.

На рис. 3 представлены графики, отражающие изменение во времени сжимающих напряжений в почве в случае ее начального деформирования по гармоническому закону (5) и их релаксацию при различных значениях влажности почвы.

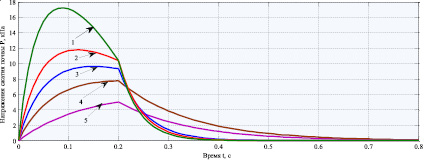
Рис. 3. Изменение во времени напряжений сжатия дерново-подзолистой легкосуглинистой почвы при ее начальном деформировании по гармоническому закону (5) и их релаксация при различных значениях влажности почвы (ε_m = 0,04, t₀ = 0,2 с, ω = 2 с^–1, ρ₀ = 1,14 г/см³); 1, 2, 3, 4 и 5 – при влажности w = 15, 16, 17, 20, 22 %.

Нами также получены кривые, характеризующие зависимости σ(t) для случая изменения e(t) при t∈[0;t₀] по закону (10). Приведенные на рис. 3 зависимости σ(t), а также другие полученные в результате расчетов данные свидетельствуют о том, что с ростом w напряжения σ(t) уменьшаются и релаксируют быстрее. Увеличение влажности почвы от 15 до 22 % приводит к снижению σ₀ при гармоническом законе начального деформирования от 16,14 до 4,65 кПа (в 3,47 раза) и напряжений σ(0,21) от 0,99 до 0,22 кПа (в 4,54 раза при ρ₀ = 1,14, ρ(0,3) = 1,7, t₀ = 0,2 с). Таким образом, исследование показало, что с ростом влажности почвы основные рассмотренные показатели убывают.

Время t₀ начального деформирования почвы оказывает существенное влияние на ее уплотнение и релаксацию напряжений. В случае изменения σ(t) по закону (5) показатели находили, варьируя t₀ от 0,15 до 0,6 с, а в случае изменения σ(t) по закону (10) – варьируя t₀ от 0,05 до 0,25 с. Расчеты показали, что с ростом t₀ величины σ₀, e₀, h₀, ∆ρ(h₀) возрастают; в процессе релаксации напряжений увеличивается время, в течение которого они становятся практически равными нулю.

При гармоническом законе (5) начального деформирования существенное влияние оказывает также амплитуда деформации em. Показатели находили, варьируя em от 0,02 до 1,2. Расчеты показали, что с ростом em величины σ₀, e₀, h₀, ∆ρ(h₀) возрастают; в процессе релаксации напряжений увеличивается время, в течение которого они становятся практически равными нулю. Увеличение em от 0,02 до 0,09 приводит к увеличению σ₀ от 3,89 до 17,50 кПа (в 4,5 раза) и напряжений σ(0,21) от 0,18 до 1,14 кПа (в 6,33 раза при ρ₀ = 1,14 г/см³, ρ(0,3) = 1,7 г/см³, t₀ = 0,2 с).

Таким образом, проведенное исследование показало, что основные рассмотренные показатели с ростом начальной плотности почвы возрастают, а с ростом влажности почвы убывают.

Отмеченный характер влияния начальной плотности почвы на ее уплотнение и релаксационные свойства обусловлен тем, что при увеличении плотности почвы характеристика вязкоупругих свойств почвы q возрастает, причем q → E, где E – модуль упругости почвы, а характеристика g убывает, причем g → 0. Свойства почвы приближаются к упругим.

Отмеченный характер влияния влажности почвы на ее уплотнение и релаксационные свойства обусловлен тем, что при увеличении w характеристика вязкоупругих свойств почвы g возрастает, а характеристика q убывает, причем q → 0. При этом упругость почвы снижается, свойства почвы приближаются к текучим.

Заключение

На основе математического моделирования вязкоупругих свойств почвы дифференциальным уравнением (2) получены аналитические зависимости и алгоритмы, позволяющие расчетным путем находить показатели напряженно-деформированного состояния почвы при различных законах начального деформирования с учетом фактора времени, а также рассчитывать приращение плотности почвы на различной глубине, возникающее в результате действия внешней нагрузки. Исследован процесс релаксации напряжений в почве. Расчеты выполнены с использованием полученных нами экспериментальных данных о вязкоупругих свойствах дерново-подзолистой легкосуглинистой почвы известного гранулометрического состава в определеном интервале изменения ее влажности.

Результаты исследования релаксационных процессов в этой почве, полученные в данной работе, согласуются с экспериментальными данными о релаксационных процессах в почвах из других опубликованных работ [2–4, 7, 11, 12] и в других деформируемых средах [10]. Поэтому прогнозирование результатов изменения напряженно-деформированного состояния и уплотнения исследованной почвы при ее начальном кратковременном деформировании и последующей релаксации напряжений в почве, выполненное на основе математического моделирования ее вязкоупругих свойств уравнением (2), можно считать адекватным.

Проведенное исследование показало, что на уплотнение почвы влияет целый ряд факторов: гранулометрический состав почвы, содержание в почве органических веществ, ее влажность, глубина распространения деформируемого слоя почвы, характер и скорость изменения деформаций, продолжительность времени деформирования и другие. Для обоснованной оценки изменения физического состояния почвы под действием внешней нагрузки нужно учитывать взаимосвязанное влияние всех этих факторов.

Необходимы исследования вязкоупругих свойств различных почв и релаксационных процессов в почвах. Полученные результаты будут полезны при разработке комплекса мер, направленных на сохранение и повышение плодородия почв.

Библиографическая ссылка