Получение показателей налоговой нагрузки экономических субъектов на микро-, мезо- и макроуровне, на основе объективных данных экономической статистики, является ключевой задачей при управлении социально-экономическим развитием территорий. Основной целью налоговой политики управляющих органов экономических субъектов при этом является получение максимального налогового дохода с учетом баланса ее экономической и социальной составляющих. При этом сохраняет актуальность не только задача разработки экономико-математического аппарата в виде математических моделей и методов их анализа, но и создание систем поддержки принятия решений в форме пакетов прикладных программ, аналитического инструментария обработки и представления соответствующей модельной и статистической информации. В данной работе описана системная концепция, позволяющая получать показатели налоговой нагрузки экономических субъектов на основе автоматизированного программного комплекса [3], созданного для анализа оптимизационной математической модели [7], в которой рассматриваются технико-экономические и бухгалтерские особенности функционирования как производственных предприятий с учетом их налогового окружения (основных видов налогов, составляющих большую часть налоговых затрат экономических субъектов), так и представляющего интересы населения региона налогового центра, в соответствии с подходом, подробно описанном в работе [6].
Следует отметить, что управление налоговой политикой на всех экономических уровнях должно осуществляться на основе математических моделей, позволяющих оценивать налоговый потенциал. Наиболее подходящими для этих целей, очевидно, являются оптимизационные модели и, в частности, модель [7]. Впрочем, для решения задачи определения оптимальной налоговой нагрузки, как результата взаимодействия производителя продукции и управляющих органов экономических субъектов, данное положение является, скорее, аксиоматическим.
Налоговые потоки являются затратными составляющими финансово-хозяйственной деятельности (ФХД) производителя. Для оценки ФХД предприятий региона целесообразно сориентироваться на разработку универсального алгоритма расчета доходных и расходных потоков, возникающих при их функционировании [5]. Кроме того, важно, чтобы указанный алгоритм, с минимальными модификациями, можно было бы адаптировать для различных уровней экономики – микро-, мезо- или макро, а также для различных типов производственной деятельности (товары и/или услуги). Ниже предлагается один из таких алгоритмов. Введем следующие обозначения:
R – выручка от продажи продукции (товаров и/или услуг) производителя;
I – инвестиционные затраты;
Z – общие производственные и налоговые затраты;
z – оборотные затраты;
Am – амортизационные отчисления;
F – фонд оплаты труда (ФОТ);
S0 – остаточная стоимость ОПФ;
N1 – налог на добавленную стоимость;
N2 – налог на имущество;
N3 – налог на прибыль;
N4 – страховые взносы предприятия (производителя);
N5 – другие налоговые (например, налог на добычу полезных ископаемых) и неналоговые (штрафы, «откаты» и пр.) затраты производителя, зависящие от объемов производства;
αi (i = 1,…,5) – соответствующие законодательно определенные ставки налоговых платежей и отчислений,
Т – горизонт планирования бизнес-проекта;
p, β – экспертно определяемые параметры, обозначающие соответственно долю оборотных затрат в общих затратах предприятия (материалоемкость производства) и долю ФОТ в выручке от продажи продукции (трудоемкость производства),
r – годовая ставка дисконтирования, учитывающая инфляцию, уровень требований инвестора и другие возможные, экспертно задаваемые, экономические и политические риски деятельности производителя.
Тогда алгоритм расчета прибыли и чистой приведенной стоимости (NPV) производителя можно представить в следующем виде [5]:
Wb = R–Z – балансовая прибыль;
Wr = (1–α3)(R–Z) – чистая прибыль,
где Z =Am + F + N1 + N2 + N4 + N5 + z;
F = βR;
z = pZ;
N1 = α1(R–pZ–I);
N2 = α2S0;
N3 = α3Wb = α3(R–Z);
N4 = α4F = α4βR;
N5 = α5R.
Ниже предлагается математическая модель, построенная на основе приведенного алгоритма, в форме двухкритериальной задачи линейного программирования:
;
;
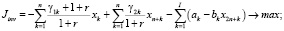
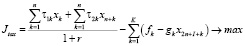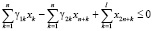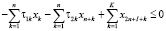; (1)
;
;
;
; 
,
,
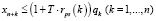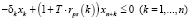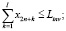
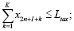
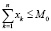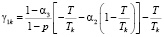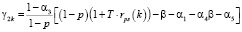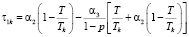
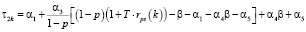где n – количество ОПФ; I, K – соответственно количество рисков для производителя и управляющего центра;
xk – стоимость приобретаемых ОПФ k-го вида (инвестиции в основные фонды);
xn+k – выручка от продажи продукции, произведенной на k-м ОПФ;
x2n+i (i = 1,…,I) – затраты на избежание (устранение) i-го риска производителя;
x2n+I+k (j = 1,…,K) – затраты на избежание (устранение) k-го риска управляющего центра;
сk – стоимость k-го ОПФ;
Pk – стоимость продукции, произведенной на k-ом ОПФ;
Vk – производительность k-го ОПФ;
Tk – время полезного использования k-го ОПФ;
qk – спрос на продукцию, произведенную на k-ом ОПФ;
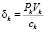– максимальная фондоотдача k-го ОПФ производственной подсистемы;
ak, fk – максимальные издержки в случае отсутствия затрат на k-ом рисковом направлении функционирования производственной и управляющей подсистем соответственно;
bk, gk – весовые коэффициенты относительной значимости k-го направления функционирования производственной и управляющей подсистем соответственно;
rps(k) – экспертно задаваемые коэффициенты, отражающие, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции;
Linv, Ltax – соответственно максимальные затраты на избежание (устранение) всех выделенных рисков производителя и управляющего центра.
Модель (1) является разновидностью предложенной в работе [7] модели, не учитывающей дотации регионального центра производителю. Кроме того, (1) одновременно обобщает модель в [7] на случай α1 ≠ 0, α5 ≠ 0. Многопараметрическая, многокритериальная задача линейного программирования (1) может решаться и анализироваться с помощью пакета программ [3], являющегося, по существу, системой поддержки принятия решений налогового аналитика, который может самостоятельно формировать структуру налоговой затратной составляющей производителя, заносить в пакет входную статистическую информацию, визуализировать решение в виде таблиц и графиков многопараметрических зависимостей, построения Парето-множеств и т.п.
Следует отметить, что приведенный выше алгоритм расчета показателей финансово-хозяйственной деятельности содержит составляющие потоки, которые позволяют рассчитывать налоговую нагрузку в соответствии с большинством известных методик – Минфина [8], М.Н. Крейниной [4], А. Кадушина-Н. Михайловой [1] и М.И. Литвина [8], – а также большую часть составляющих методики Е.А. Кировой [2]. Вместе с тем отметим, что недостающие в модели (1) составляющие, связанные с внереализационными налоговыми потоками, вряд ли целесообразно использовать в прогнозно-аналитических моделях бизнес-планирования деятельности предприятий.
Результаты расчетов позволят налоговому аналитику принимать обоснованные решения по управлению региональной налоговой политикой, исходя из принципиальной возможности оценки налогового потенциала Jtax и налоговой нагрузки экономических субъектов, рассчитываемой по указанным выше методикам.
Библиографическая ссылка
Медведев А.В. ОЦЕНКА НАЛОГОВОЙ НАГРУЗКИ НА ОСНОВЕ ОПТИМИЗАЦИОННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 8-4. – С. 720-722;URL: https://applied-research.ru/ru/article/view?id=7228 (дата обращения: 23.11.2024).