Хорошо известен и во многих ситуациях полезен так называемый «принцип диагонали» – для всякой последовательности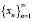 
, сходящейся к точке x∈X топологического пространства и всяких последовательностей 
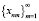, сходящихся к точке xn, n∈N, найдется подпоследовательность 
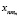, сходящаяся к точке x.
В данной работе рассматриваются классы топологических пространств, такие как метрические, квазиметрические, пространства с первой аксиомой счетности, пространства Фреше–Урысона и другие, то есть такие, где топология полностью описывается сходящимися последовательностями. В этих пространствах, а также и в более общей ситуации, изучается «принцип диагонали» и некоторые его ослабления. Рассматривается вопрос, когда справедлив «принцип диагонали»? Этот вопрос, в частности, интересен и потому, что к нему (или к близким вопросам) приводит общая задача, когда семейство сходящихся последовательностей в том или ином классе топологических пространств порождается некоторой метрикой (квазиметрикой, симметрикой и т.д.). Получены конкретные результаты в этом направлении, в частности, доказана следующая
Теорема. Топологическое пространство X удовлетворяет условию Фреше–Урысона тогда и только тогда, когда X – секвенциальное пространство, в котором выполняется «принцип диагонали».
Библиографическая ссылка
Хохлов А.Г., Шалагинов С.Д. К ВОПРОСАМ СХОДИМОСТИ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ // Международный журнал прикладных и фундаментальных исследований. 2015. № 8-5. С. 974-974;URL: https://applied-research.ru/ru/article/view?id=7287 (дата обращения: 05.04.2025).