О численном методе, алгоритме и комплексе программ моделирования волн напряжений
В работах [1–10] приведена информация о нестационарных волнах напряжений в сложных деформируемых телах.
При динамическом и импульсном воздействии в сооружении распространяются волны напряжений.
Для решения задачи о моделировании нестационарных упругих волн в деформируемых областях сложной формы рассмотрим некоторое тело Г в прямоугольной декартовой системе координат ХОУ, которому в начальный момент времени t = 0 сообщается механическое воздействие. Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
,
,
, 
,
, 
,
, 
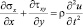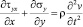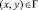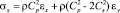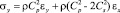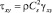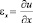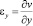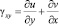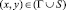, (1)
где σx, σy и τxy – компоненты тензора упругих напряжений;
εx, εy и γxy – компоненты тензора упругих деформаций;
u и v – составляющие вектора упругих перемещений вдоль осей ОХ и OУ соответственно;
ρ – плотность материала;
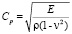– скорость продольной упругой волны;
– скорость поперечной упругой волны;
v – коэффициент Пуассона;
Е – модуль упругости;
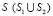– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях. Задача решается методом сквозного счета, без выделения разрывов. Чтобы выполнить динамический расчет методом конечных элементов, нужно иметь матрицу жесткости и матрицу инерции конечного элемента.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
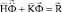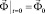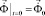, (2)
где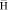 
– матрица инерции;
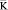– матрица жесткости;
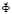– вектор узловых упругих перемещений;
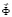– вектор узловых упругих скоростей перемещений;
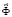– вектор узловых упругих ускорений;
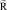– вектор узловых упругих внешних сил.
Соотношение (2) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши (2).
Для интегрирования уравнения (2) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
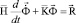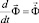. (3)
Интегрируя по временной координате соотношение (3) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
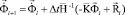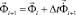. (4)
где ∆t – шаг по временной координате.
Система уравнений (2) для внутренних и граничных узловых точек, полученная в результате интегрирования уравнения движения теории упругости, должна давать решение, сходящееся к решению исходной системы (1).
Шаг по временной переменной ∆t определяем из следующего соотношения
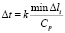
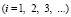, (5)
где ∆l – длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы.
Некоторая информация о физической достоверности и математической точности моделирования нестационарных волн напряжений в деформируемых телах с помощью рассматриваемого численного метода, алгоритма и комплекса программ приведена в следующих работах [1–2, 4–6, 8, 10].
Решение задачи о воздействии плоской продольной упругой волны в виде треугольного импульса на бесконечную полосу
Рассмотрим задачу о воздействии плоской продольной упругой волны в виде треугольного импульса (рис. 1) на бесконечную полосу (рис. 2).
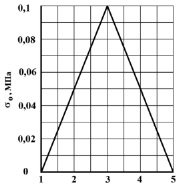
Рис. 1. Воздействие в виде треугольного импульса
На границе пластинки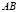 
(рис. 2) приложено нормальное напряжение σy (рис. 1), которое при 1 ≤ n ≤ 3 (n = t/∆t) изменяется линейно от 0 до P, а при 3 ≤ n ≥ 5 от P до 0 (P = σ0, σ0 = – 0,1 МПа). Граничные условия для контуров BC и AD при t > 0 
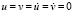. Отраженные волны от контуров BC и AD не доходят до исследуемых точек. Контур CD свободен от нагрузок. Исследуемая расчетная область имеет 4002 узловые точки. Решается система уравнений из 16008 неизвестных.
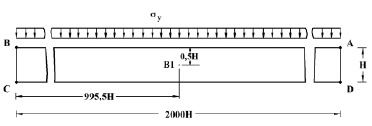
Рис. 2. Постановка задачи о стоячих волнах в бесконечной полосе
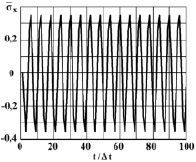
Рис. 3. Нормальное напряжение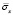 
во времени 0 ≤ n ≤ 100 в точке B1
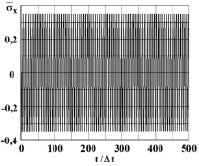
Рис. 4. Нормальное напряжение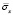 
во времени 0 ≤ n ≤ 500 в точке B1
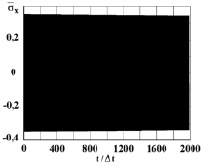
Рис. 5. Нормальное напряжение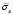 
во времени 0 ≤ n ≤ 1990 в точке B1
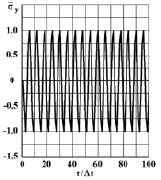
Рис. 6. Нормальное напряжение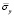 
во времени 0 ≤ n ≤ 100 в точке B1
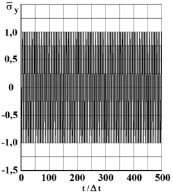
Рис. 7. Нормальное напряжение 
во времени 0 ≤ n ≤ 500 в точке B1
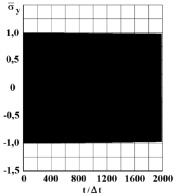
Рис. 8. Нормальное напряжение 
во времени 0 ≤ n ≤ 1990 в точке B1
Для примера на рис. 3–5 представлено изменение нормального напряжения 
(
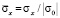) во времени n в точке B1.
Для примера на рис. 6–8 представлено изменение нормального напряжения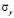 
(
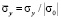) во времени n в точке B1.
Получены нормальные напряжения в характерной области бесконечной полосы. Отраженные волны от свободных поверхностей бесконечной полосы создают физическую картину стоячих волн.
Библиографическая ссылка
Мусаев В.К. МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ СТОЯЧИХ УПРУГИХ ВОЛН В БЕСКОНЕЧНОЙ ПОЛОСЕ ПРИ ВОЗДЕЙСТВИИ В ВИДЕ ТРЕУГОЛЬНОГО ИМПУЛЬСА // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 9-2. – С. 248-251;URL: https://applied-research.ru/ru/article/view?id=7301 (дата обращения: 21.11.2024).