В настоящее время наблюдается бурное развитие информационных технологий и их внедрение в самые различные сферы деятельности человека. Сети передачи данных [1] стали неотъемлемой частью жизни людей, без которой практически немыслим информационный обмен. В такой ситуации анализ технических характеристик существующих сетей передачи данных и проектирование новых сетей с учетом заданных характеристик остается одной из актуальных задач в области информационных технологий.
Помимо таких технических характеристик компьютерных сетей, как: производительность, время задержки, безопасность, масштабируемость, крайне важными характеристиками являются комплексные показатели надежности: коэффициент готовности и среднее время недоступности в год [2, 3].
От показателей надежности напрямую зависит доступность информационных сервисов для пользователей. Кроме того, от надежности сети косвенно также зависят производительность и латентность сети, поскольку возникновение сбоев и отказов в сети ведет к необходимости повторной передачи блоков данных, а это в итоге ведет к увеличению задержек при передаче и уменьшению объемов передаваемых данных в единицу времени. Наконец, от надежности сети также косвенно зависит безопасность функционирования систем управления какими-либо объектами, в которых несвоевременная реакция (из-за отказов и сбоев в сети передачи данных) системы управления на какие-либо критические изменения в объекте управления могут привести к серьезным последствиям. В такой ситуации анализ показателей надежности сетей передачи данных является особенно актуальной проблемой.
В рамках научных исследований автора [4–10] было рассмотрено применение теоретической модели надежности восстанавливаемых систем, состоящих из множества идентичных независимых объектов, на трехуровневых локальных сетях передачи данных.
Модель надежности группы независимых элементов. Пусть имеется n идентичных восстанавливаемых элементов с одинаковыми интенсивностями отказов λ и восстановления μ. Элементы могут независимо отказывать и независимо восстанавливаться без каких-либо ограничений. Тогда получаем марковскую модель надежности (рис. 1).

Рис. 1. Модель надежности группы независимых восстанавливаемых элементов
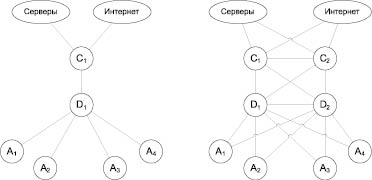
Рис. 2. Трехуровневые локальные сети с одним (схема слева) и с двумя (схема справа) коммутаторами ядра и распределения, и с 4 коммутаторами доступа
Математическая модель (система уравнений Колмогорова–Чепмена):
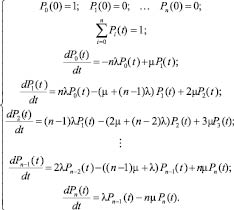
Общее решение системы дифференциальных уравнений в аналитическом виде выглядит следующим образом:
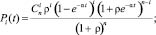
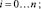
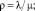
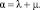 (1)
(1)
При t → ∞ марковский процесс становится установившимся, и вероятности уже не меняются с течением времени:
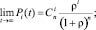
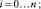
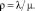
Трехуровневые локальные сети. В трехуровневых сетях передачи данных (рис. 2) можно выделить три независимые с точки зрения модели надежности группы объектов – группа коммутаторов уровня ядра, группа коммутаторов уровня распределения и группа коммутаторов уровня доступа.
Сеть содержит r ≥ 1 коммутаторов ядра (Core), s ≥ 1 коммутаторов распределения (Distribution) и k ≥ 1 коммутаторов уровня доступа (Access). Серверы локальной сети и сети Интернет доступны через каждый коммутатор ядра. Коммутаторы ядра и коммутаторы распределения связаны между собой каждый с каждым. Коммутаторы доступа между собой не связаны, но связаны с каждым коммутатором распределения. Отказ любого коммутатора доступа, также как и нарушение связи любого коммутатора доступа с серверами или сетью Интернет, считается отказом всей сети целом.
Модель надежности трехуровневой сети. Коммутаторы уровня ядра имеют интенсивность отказов λC и интенсивность восстановления μC, коммутаторы уровня распределения имеют интенсивность отказов λD и восстановления μD, коммутаторы уровня доступа имеют интенсивность отказов λA и восстановления λA.
Что касается группы коммутаторов ядра, то поскольку каждый из них связан с каждым с коммутатором распределения и каждый связан с серверами и сетью Интернет, то сеть считается работоспособной при первом условии, что хотя бы один коммутатор в группе коммутаторов ядра работоспособен. Вероятность этого равна сумме вероятностей от нулевого состояния до предпоследнего состояния в марковской модели надежности группы из r независимых объектов:
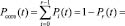
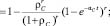
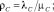
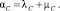
Что касается группы коммутаторов распределения, то поскольку каждый из них связан с каждым с коммутатором ядра и с каждым коммутатором уровня доступа, то сеть считается работоспособной при втором условии, что хотя бы один коммутатор в группе коммутаторов распределения работоспособен. Вероятность этого равна сумме вероятностей от нулевого состояния до предпоследнего состояния в марковской модели надежности группы из s независимых объектов:
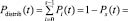
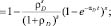
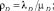
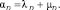
Наконец, поскольку отказ любого коммутатора доступа считается отказом всей сети в целом, то очевидно, сеть считается работоспособной при третьем условии, что все k коммутаторов в группе коммутаторов доступа работоспособны. Вероятность этого равна вероятности нулевого состояния в марковской модели надежности группы из k независимых объектов:
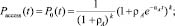
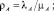
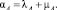
Объединим три условия работоспособности сети, перемножив их вероятности, и получим окончательную формулу для вероятности работоспособности двухуровневой сети в целом:
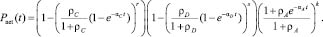
Тогда стационарный коэффициент готовности трехуровневой сети:
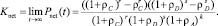 (2)
(2)
Пример расчета коэффициента готовности. Пусть имеется двухуровневая сеть из k = 6 коммутаторов доступа, s = 1 коммутатора распределения и r = 1 коммутатора ядра.
С целью повышения отказоустойчивости сети был внедрен второй коммутатор ядра (r = 2) и второй коммутатор распределения (s = 2).
Интенсивность отказов коммутатора ядра λC = 1/8760 час-1, а интенсивность восстановления μC = 1/24 час-1. Интенсивность отказов коммутатора распределения λD = 1/8760 час-1, а восстановления μD = 1/6 час-1. Интенсивность отказов коммутатора доступа λA = 1/8760 час-1, а восстановления μA = 1 час-1.
Оценим коэффициент готовности сети до и после ее модернизации.
Решение. Имеем ρC = λC/μC = 1/365, ρD = λD/μD = 1/1460, ρA = λA/μA = 1/8760.
Тогда коэффициент готовности до модернизации сети (r = 1, s = 1, k = 6) составит:
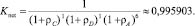
А после модернизации сети (r = 2, s = 2, k = 6) коэффициент готовности составит:
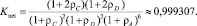
Если оценить среднее количество часов недоступности сети в год (8760 часов) по формуле 8760(1 – Knet), то до модернизации имеем около 36 часов недоступности в год, а после – около 6 часов в год.
Заключение
Таким образом, в рамках данной статьи была рассмотрена модель надежности трехуровневых локальных сетей передачи данных. Также были приведены формулы и примеры расчета коэффициента готовности сетей и среднего времени недоступности в год. Полученные теоретические результаты использовались в многолетней практике эксплуатации, развития и проектирования сетей среднего масштаба НИУ МЭИ (ТУ), ОАО «Красный Пролетарий» и ряда других предприятий.
Библиографическая ссылка
Рахман П.А. КОЭФФИЦИЕНТ ГОТОВНОСТИ ТРЕХУРОВНЕВЫХ ЛОКАЛЬНЫХ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ // Международный журнал прикладных и фундаментальных исследований. 2015. № 9-3. С. 463-466;URL: https://applied-research.ru/ru/article/view?id=7349 (дата обращения: 05.01.2026).

