Задача прогнозирования временных рядов (ВР) и, в частности, электропотребления не теряет своей актуальности на протяжении уже многих лет. В точном прогнозе электрической нагрузки заинтересованы и поставщики, и потребители электроэнергии, т.к. это позволяет минимизировать издержки обеих сторон. Большинство современных публикаций, посвященных данной проблеме, сконцентрированы на разработке и усовершенствовании новых информационных технологий прогнозирования временных рядов, таких нейронные, нечеткие сети, генетические алгоритмы и пр. Это объясняется способностью данных методов осуществлять прогноз в таких условиях как: неопределенность исходных данных (наличие телеметрических искажений), недостаточность априорной информации, сложное нестационарное поведение прогнозируемого временного ряда.
Временной ряд, описывающий электропотребление в полной мере отвечает перечисленным особенностям, именно поэтому предлагаемая система краткосрочного прогнозирования построена на базе интеллектуальных вычислительных технологий. Этапы синтеза системы прогнозирования потребления электрической нагрузки изложены ниже.
Исходными данными для анализа и прогнозирования являются почасовые значения объемов покупки электроэнергии на оптовом рынке электроэнергии и мощности для первой ценовой зоны (Европа и Урал) за рабочие дни января-февраля 2004 года. В качестве обучающих данных используются значения почасового электропотребления за первые 14 рабочих дней февраля 2004 года. Максимальный разброс данных обучающей выборки составляет 30 %.
Анализ исходной информации по электропотреблению позволил сформулировать рабочую гипотезу о целесообразности разделения исходного ВР на характерные разночастотные аддитивные компоненты, подбора для них метода прогнозирования и последующее объединение спрогнозированных составляющих для получения итоговой прогнозной оценки.
Выделение аддитивных компонент осуществляется при помощи вейвлет-преобразования. В качестве метода прогнозирования для каждой составляющей временного ряда выбрана нечеткая математическая модель на основе алгоритма Такаги-Сугено, параметры которой настраиваются при помощи адаптивной нейро-нечеткой сети ANFIS [3, 4]. Для построения ННС выбрана функция genfis2, которая производит более экономичное разбиение пространства входов на подобласти и является более эффективным инструментом для выявления правил из набора экспериментальных данных. По результатам исследований системы прогнозирования, построенной с помощью функции gеnfis2, можно сделать следующие выводы:
– явным преимуществом по сравнению с выходом-константой обладает линейный выход гибридной сети (средняя ошибка прогнозирования составила – 2.62 % (для линейного выхода), а для константы – 6.12 %);
– с точки зрения качества и скорости обучения наилучшими являются колоколообразная, Гауссова и трапецеидальная функции принадлежности (ФП); Анализ влияния типа функций принадлежности по каждому входу на качество прогнозирования выявил следующие показатели: среднюю ошибку обучения для колоколообразной ФП – 2,62 %; для треугольной ФП – 5,0 %; для Гауссовой ФП – 2,5 % и для разности двух Гауссовых функций – 2,79 %; для ПИ-образной ФП – 5,87 %; для произведения двух сигмоидальных функций – 6,82 % и, наконец, для трапецеидальной ФП – 3,5 %.
– увеличение числа уроков обучения, а также числа функции принадлежности для каждого входа при не всегда существенном увеличении точности обучения, приводит к значительным временным затратам на обучение сети и даже к ее полной неработоспособности;
– увеличение числа входов модели также приводит к сбою в работе ННС, максимальное число входов, при котором система не теряет работоспособность – 8,10.
– варьируя радиус кластеризации как для всех входных переменных, так и для каждой в отдельности, можно добиться увеличения точности прогноза. При этом если назначить величину радиуса кластеризации слишком маленьким, генерируется слишком большое число правил и сеть становиться неработоспособной. Значения радиусов кластеризации в каждом конкретном случае определяется эмпирически. Этот параметр является ключевым при построении ННС.
Таким образом, типовая структура системы прогнозирования представляет собой комитет из ННС, осуществляющих процедуру прогнозирования для нескольких каналов данных, полученных при помощи вейвлет-фильтрации исходного временного ряда. Данные статистик почасового потребления поступают на вход системы прогнозирования через пользовательский интерфейс. В качестве дополнительной информации на вход системы прогнозирования поступает информация о номере часа, для которого осуществляется прогнозирование. Разработана программа, реализующая модифицированный метод окон для автоматического формирования входных переменных, обучающей и тестовой последовательностей, для систем с различным числом входов и выходов, что существенно облегчает процедуру модификации ННС.
Для реализации процедуры переобучения нейронечетких моделей в случае превышения ошибки прогнозирования допустимой нормы (3 %), разработан блок оптимизации структур на основе генетического алгоритма. Программа находит наилучшую структуру ННС, при которой система дает наименьшую ошибку прогнозирования [2].
Функционирование типовой системы прогнозирования потребления электрической нагрузки осуществляется в следующей последовательности:
1) задание ретроспективных данных по нагрузке (минимум за последние 9 часов) и номера часа прогнозирования через интерфейс системы;
2) вейвлет-фильтрация данных по нагрузке и получение на выходе блока фильтрации четырех векторов, соответствующих разночастотным составляющим исходных данных;
3) формирование входных векторов для ННС при помощи специального программного блока;
4) прогнозирование нагрузки на час вперед по каждой составляющей вейвлет-разложения в отдельности;
5) суммирование полученных прогнозов и вывод результата.
Представляет интерес сравнительный анализ построенной системы прогнозирования с регрессионными моделями и с системой прогнозирования также основанной на ННС, но без предварительной вейвлет-фильтрации. Также планируется провести оценку устойчивости модели к возможным неточностям входной информации.
Поскольку обучение ННС и прогнозирование осуществляется для каждой компоненты ВР в отдельности, целесообразно оценить точность прогнозирования как каждого уровня вейвлет-разложения, так и системы в целом. Для глубины вейвлет-разложения равной трем средняя точность прогнозирования составляет: для уровня аппроксимации – 0,56 %, для детализации на уровне 3 – 3,54 %, для детализации на уровне 2 – 4,13 %, для детализации на уровне 1 – 6,26 %. Суммарная точность прогнозирования равна 1,6 %.
Не смотря на то, что точность прогнозирования для некоторых уровней детализации является невысокой, суммарное приближение к фактическому значению нагрузки выше при использовании разложения по вейвлету и прогнозированию каждой составляющей. Это объясняется тем, что нет необходимости в подборе такой архитектуры нечеткой нейронной сети, которая учитывала бы динамику изменения одновременно быстроменяющейся и медленноменяющейся компонент временного ряда. Точный учет изменения детальных компонент временного ряда (быстроменяющаяся компонента) дает плохую способность сети к обобщению, что приводит к значительным ошибкам прогнозирования как и при недостаточном обучении сети (игнорирование быстроменяющейся компоненты).
Точность оценивается как абсолютная средняя ошибка
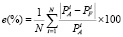 ,
,
где PA – фактическое значение нагрузки, PF – результат восстановления (прогноза) и N – количество данных (часов).
Кроме того, были проведены исследования на чувствительность данного подхода в прогнозировании к возможной неточности входной информации, поскольку данные телеметрических измерений, поступающие на вход систем прогнозирования содержат некоторую ошибку.
Отсюда возникает вопрос о работоспособности модели при искажении входной информации. Для этого на вход системы подавалась намеренно искаженная входная информация. Полученные в результате прогнозирования данные затем сравнивались с реальными значениями. Результаты исследований приведены в таблице.
Как видно из анализа таблицы, сильнее всего искажение данных оказывает влияние на ошибку детализирующих уровней, а особенно на ошибку уровней детализации 1 и 2, отвечающих за быструю динамику ВР.
Это объясняется тем, что входные данные искажались высокочастотным шумом, который отфильтровывался вейвлет-преобразованием на детализирующие (высокочастотные) компоненты. На рисунке видно, что показатель Херста [1] для этих двух составляющих (ряд 1 и 2 на рисунке) снижается гораздо резче, чем для первых двух (аппроксимация – ряд 4 и детализация 3 – ряд 3).
Как видно из анализа таблицы, при искажении входных данных до 7 % (по MAPE), модель все еще выдает более или менее адекватный прогноз. Затем происходит резкое ухудшение прогнозных качеств модели, когда вейвлет-преобразование с глубиной разложения 3 уже не в состоянии отфильтровать высокочастотную составляющую на уровне аппроксимации и детализации 3. При этом показатель Херста Н падает с 0,73 до 0,72. Таким образом, этот интервал можно считать критическим для построенной модели.
Результаты прогнозирования при искажении входных данных
|
Искажение шумом, % |
Н |
MAPE, % аппрокс. |
MAPE, % детал. 3. |
MAPE, % детал. 2. |
MAPE, % детал. 1. |
MAPE, % прогноза |
|
0 |
0,73 |
0,56 |
2,54 |
4,13 |
6,26 |
1,86 |
|
1,38 |
0,73 |
0,70 |
5,22 |
6,45 |
10,74 |
2,69 |
|
2,77 |
0,73 |
0,93 |
7,23 |
11,59 |
13,66 |
3,95 |
|
4,15 |
0,73 |
1,17 |
9,81 |
16,24 |
24,11 |
5,22 |
|
5,54 |
0,72 |
1,39 |
10,43 |
31,10 |
54,09 |
12,36 |
|
6,92 |
0,72 |
1,61 |
30,06 |
122,50 |
261,8 |
56,16 |
|
8,31 |
0,71 |
1,89 |
33,60 |
174,22 |
225,10 |
57,30 |
|
9,69 |
0,70 |
2,11 |
126,38 |
276,40 |
1161,30 |
58,42 |
|
11,08 |
0,69 |
2,41 |
299,65 |
321,02 |
223,93 |
50,89 |
|
12,47 |
0,68 |
2,62 |
247,63 |
167,29 |
1711,50 |
59,03 |
|
13,85 |
0,67 |
2,83 |
85,60 |
1967,20 |
337,89 |
64,91 |

Динамика изменения показателя Херста при искажении данных шумом
Анализ остатков модели электропотребления показал, что предъявляемые к ним требования выполняются:
1) у стандартизированных остатков отсутствуют ярко выраженные выбросы, и они распределены по нормальному закону с однородной дисперсией;
2) отсутствуют сериальные корреляции остатков, которые являются белым шумом, а дисперсия, обусловленная регрессией, значимо больше дисперсии остатков, что является подтверждением адекватности разработанной модели.
Был проведен сравнительный анализ предложенной методики прогнозирования с прогнозированием, выполненным по регрессионным моделям. Для всех исследованных линейных (по параметрам) моделей невозможно получить точность прогнозирования выше 3,5 % в приемлемых границах 95 % доверительного интервала. Увеличение числа регрессоров приводит к увеличению границ доверительного интервала для прогнозируемых значений и ухудшению прогнозных свойств модели вплоть до потери работоспособности. Кроме того, работоспособность модели утрачивается при попытке прогнозирования на 2 и более часов вперед, поскольку точность прогнозирования объясняется близостью требуемых прогнозируемых величин к предыстории (прогноз на час вперед).
Наилучшие результаты при прогнозировании на час вперед были получены для модели ARMA (20,10). Точность прогнозирования составила 2,7 %. Для нейронечеткой модели с использованием вейвлет-теории точность прогнозирования при тех же условиях (прогнозирование на час вперед, одинаковая обучающая выборка) составляет 1,6 %.
Для применения статистических моделей требуется большой набор экспериментальных данных (достаточных для определения характера распределения) и возможность приведения нестационарного процесса (каким является режим электропотребления) к стационарному. Пика нагрузки можно ожидать как в первой, так и во второй половине дня. Изменение во времени нагрузки представляет собой слабо коррелированный (нестационарный) случайный процесс, что может привести к снижению точности прогноза при использовании традиционных методов.
Также были проведены сравнительные исследования точности прогнозирования для построенной системы и модели прогнозирования на основе ННС без предварительной вейвлет-фильтрации.
Для этого при помощи ГА была выбрана наилучшая структура ННС, дающая наибольшую точность прогнозирования.
Нечеткий регулятор, в соответствии, построен на основе правил нечеткого логического выхода Такаги-Сугено. При фаззификации были выбраны Гауссовы функции принадлежности. Результирующая точность краткосрочного прогнозирования при использовании вейвлет-преобразования выше, чем без него. Точность прогнозирования для ННС с использованием вейвлет-преобразования – 1,6 %; для ННС – 2,1 %.
При искажении исходных данных на 3 % точность прогнозирования составила для ННС с использованием вейвлет-преобразования – 4 %; для ННС – 4,5 %, АРСС – 6,3 %. Отсюда можно сделать вывод, что предложенная система прогнозирования обладает более устойчивым характером работы, по сравнению с классическими алгоритмами.
Кроме того, по сравнению с ННС без использования ВП построенная модель также характеризуется меньшей погрешность прогноза. Это объясняется тем, что отфильтрованные на высокие уровни детализации высокочастотные искажения имеют меньший масштаб и ошибка прогнозирования для этих ВР вносит наименьший вклад в общую ошибку прогноза.
Для предложенной системы прогнозирования разработан пользовательский интерфейс, позволяющий осуществлять процедуру прогнозирования как в пользовательском (ручном), так и в автоматическом режиме.
Управляющая программа работает в двух режимах: коррекция и моделирование; просмотр и прогнозирование. В режиме коррекции и моделирования автоматически при помощи ГА осуществляется настройка прогнозной модели по ретроспективным данным ЭП, заданным оператором. В режиме просмотра и прогнозирования происходит непосредственно расчет прогнозируемого значения нагрузки, а также реализован графический просмотр результатов прогнозирования.
В программе предусмотрена возможность сохранения и печати результатов прогнозирования в текстовом и графическом виде и ручной коррекции прогноза путем исключения из расчета выбранных уровней детализации ВР.
Работа выполнена при финансовой поддержке гранта Президента Российской Федерации № 14.Z56.14.3734-МК.
Библиографическая ссылка
Филатова Е.С., Филатов Д.М., Стоцкая А.Д. СИСТЕМА КРАТКОСРОЧНОГО ПРОГНОЗИРОВАНИЯ ЭЛЕКТРОПОТРЕБЛЕНИЯ // Международный журнал прикладных и фундаментальных исследований. 2015. № 10-1. С. 46-50;URL: https://applied-research.ru/ru/article/view?id=7380 (дата обращения: 03.01.2026).

