Очевидно, что требование детерминированности входных данных является неоправданным упрощением реальности, так любой инвестиционный проект характеризуется множеством факторов неопределенности [6].
Теория нечетких множеств позволяет более детально интерпретировать результаты наблюдений, полученных опытным путем, т.к. дает исследователю основания для анализа неоднородных и недостаточных выборок, которые классическая теория вероятности законно игнорирует [7].
В [4] предложен альтернативный подход, базирующийся на включении в модель описания экспертного понимания природы этих параметров в нечеткой форме. Автор предлагает рассматривать входящие параметры как нечеткие числа с соответствующим инструментарием их анализа.
Используя этот подход и описанную модель [1–3], в данной статье приводятся расчеты задачи оптимального финансирования инвестиционных проектов, позволяющей максимизировать получаемый предприятием доход с использованием параметров в форме нечетких множеств.
Задача оптимального финансирования инвестиционных проектов, позволяющая максимизировать получаемый предприятием доход
Дадим ряд определений, используемых в данной работе [4].
Опр. Нечеткое подмножество А множества Х – это семейство подмножеств 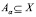 где
где 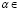 в [0,1], обладающее следующими свойствами:
в [0,1], обладающее следующими свойствами:
1. А0 = Х обладающее следующими,
2. 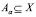 , если
, если 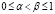 ,
,
3. 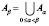 .
.
Нечеткое подмножество А множества Х называется нечетким множеством.
Нечёткое множество A задаётся посредством функции принадлежности. Значение есть число, лежащее между 0 и 1, показывающее степень принадлежности элемента x нечёткому множеству A [5].
Опр. Пусть 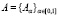 – нечеткое подмножество из Х. Функция определяемая как
– нечеткое подмножество из Х. Функция определяемая как 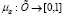 , определяемая как:
, определяемая как:
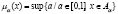 ,
,
называется функцией принадлежности, а ее значения 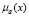 степенью принадлежности х нечеткому множеству А.
степенью принадлежности х нечеткому множеству А.
Равенство 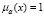 означает, что x точно принадлежит множеству A; равенство
означает, что x точно принадлежит множеству A; равенство 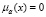 говорит о том, что x точно не принадлежит множеству A. Т. о. нечёткие множества отличаются от обычных множеств тем, что допускают промежуточные степени принадлежности, например,
говорит о том, что x точно не принадлежит множеству A. Т. о. нечёткие множества отличаются от обычных множеств тем, что допускают промежуточные степени принадлежности, например, 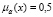 .
.
Далее мы будем предполагать, что нечёткое множество A нормировано, т.е. существует такой элемент x, что 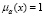 .
.
Для любого числа α, 0<α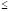 1 α-срезом нечёткого множества A называется подмножество
1 α-срезом нечёткого множества A называется подмножество 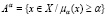 . 1-срез называют ядром нечёткого множества A. Заметим, что нечёткое множество однозначно восстанавливается по своим срезам.
. 1-срез называют ядром нечёткого множества A. Заметим, что нечёткое множество однозначно восстанавливается по своим срезам.
Когда X=R – множество вещественных чисел, говорят о нечётких числах. Для практических вычислений удобно работать с треугольными числами.
Пусть, а=(аL, аC, аR) – треугольное нечеткое число и аL<аC<аR, где аL – называется левым значением числа а, аC – средним, а аR – правым значением числа а. Тогда функция принадлежности задается выражением:
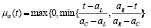 (1)
(1)
Примечание: любое действительное число можно представить в виде нечеткого, при условии, что аL=аC=аR
Нечёткие числа можно складывать, вычитать, умножать и делить, как и обычные числа [4]. Операции на нечётких числах определяются посредством следующего принципа расширения: Пусть 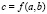 – произвольная числовая функция, например, функция сложения
– произвольная числовая функция, например, функция сложения 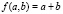 . Тогда значение
. Тогда значение 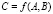 этой функции на нечётких числах A и B имеет функцию принадлежности, вычисляемую по следующей формуле:
этой функции на нечётких числах A и B имеет функцию принадлежности, вычисляемую по следующей формуле:
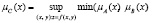
В этом случае α-срезы нечёткого множества C имеют вид:
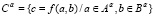
Применяя принцип расширения к арифметическим операциям и трапециевидным нечётким числам, мы получим следующие правила сложения и вычитания:
(аL, аC, аR)+ (bL, bC, bR)= (аL+ bL, аC+ bC, аR+ bR).
Рассмотрим случай, когда предприятие рассматривает различные инвестиционные проекты. Через 7 месяцев ему необходимо получить доход размером в 2 000 000 рублей, при этом возвратность кредита через 3 месяца должна составить 900 000 долларов [1-3]. Процент прибыли по каждому из проектов четко не определен и представим в виде треугольных нечетких чисел.
Задача состоит в том, чтобы найти стратегию максимизации величины ресурсов в конце данного семилетнего периода. Эта задача оптимального инвестирования может быть сформулирована как задача нечеткого линейного программирования с целевой функцией:
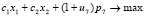 (2)
(2)
при ограничениях:
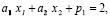
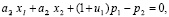
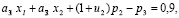
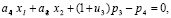
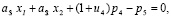 (3)
(3)
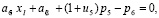
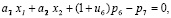
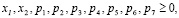
где сi – нечеткий доход от i-го проекта, i=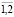 , в j-ом году, j=
, в j-ом году, j=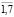 ; aij – нечеткий доход/затраты от i-го проекта, i=
; aij – нечеткий доход/затраты от i-го проекта, i=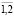 , в j-ом году, j=
, в j-ом году, j=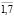 ; ui – нечеткая процентная ставка в j-ом году, j=
; ui – нечеткая процентная ставка в j-ом году, j=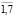 ; хi – мера участия в i-ом проекте, i=
; хi – мера участия в i-ом проекте, i=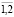 ; pj – распределение ресурсов в j-ом году, j=
; pj – распределение ресурсов в j-ом году, j=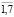 ; «+» – расширенное сложение [4]; «=» – отношение нечеткого равенства.
; «+» – расширенное сложение [4]; «=» – отношение нечеткого равенства.
Будем предполагать, что рассмотренные параметры являются треугольными нечеткими числами следующего вида:
|
с1=(4,6,8), с2=(3,5,7), a11=(6,10,14), a12=(3,6,9), a21=(-4,-2,0), a22=(1,2,3), a31=(6,8,10), a32=(6,12,18), |
a41=(7,8,9), a42=(6,10,14), a51=(3,5,7), a52=(8,9,10), a61=(6,11,16), a62=(7,10,13), a71=(6,8,10), a72=(3,5,7), |
u1=(0,001;0,002; 0,003), u2=(0,001;0,002; 0,003), u3=(0,001;0,003; 0,005), u4=(0,002;0,004; 0,006), u5=(0,001;0,004; 0,007), u6=(0,003;0,004; 0,005). |
Пусть 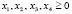 , исключая случай
, исключая случай 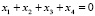 , т.е. исключается ситуация, при которой инвестор не участвует ни в одном проекте.
, т.е. исключается ситуация, при которой инвестор не участвует ни в одном проекте.
По принципу расширения левые части ограничений (2), являются треугольными нечеткими числами следующего вида [4]:
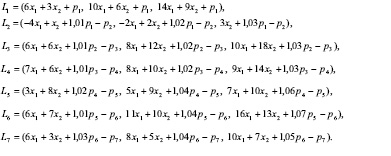 Применяя (1) вычислим функции принадлежности для
Применяя (1) вычислим функции принадлежности для 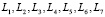 :
:
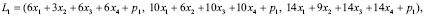
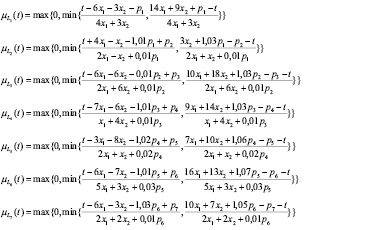
Допустимое решение задачи нечеткого линейного программирования (3) является нечетким множеством, определенным функции принадлежности:
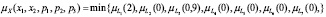
Используя методику [4] найдем допустимые решения задачи:
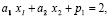
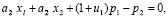
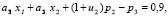
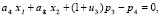 (4)
(4)
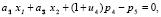
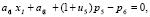
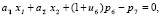
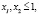
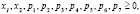
Удовлетворяющее решение будет иметь вид:
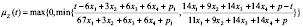
Чтобы найти max-удовлетворяющее решение это множество векторов х*=(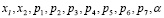 ), для которых выполняется условие (4).
), для которых выполняется условие (4).
Применение пакета Microsoft Office Solver позволило вычислить следующее оптимальное решение задачи (2)-(3).
Таким образом, формулировка задачи нечеткого линейного программирования позволяет находить оптимальное решение в условиях неопределенности параметров модели, а так же дает учитывать различные требования.
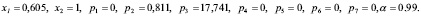
Библиографическая ссылка
Шаталова А.Ю., Лебедев К.А. НЕЧЕТКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ В ЗАДАЧЕ ОПТИМАЛЬНОГО ФИНАНСИРОВАНИЯ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ, МАКСИМИЗИРУЮЩЕЙ ПОЛУЧАЕМЫЙ ПРЕДПРИЯТИЕМ ДОХОД // Международный журнал прикладных и фундаментальных исследований. 2015. № 9-1. С. 35-38;URL: https://applied-research.ru/ru/article/view?id=7434 (дата обращения: 09.02.2026).

