Введение
В игровых видах спорта от спортсмена требуется быстрая оценка соревновательных ситуаций, принятие адекватных решений и техническое мастерство при выполнении двигательных действий [1]. В работе [5] отмечается, что эффективность двигательных действий зависит от моторных возможностей, обусловленных быстротой, и точностью движений, под которой понимают точность пространственных, временных и силовых характеристик движения.
При оценке вероятной успешности спортсмена тренеры (тренерский совет, психологи и другие специалисты) ориентируются на данные наблюдений за характером его действий в тренировочных играх, данные субъективной оценки психоэмоциональной напряженности и мотивационных установок, результаты психофизиологического тестирования и поведенческие реакции. По результатам оценки выносится суждение об ожидаемых спортивных результатах и решение о включении спортсмена в команду для участия в ответственных предстоящих соревнованиях. Однако такая оценка характеризуется выраженным субъективизмом и поэтому часто оказывается недостаточно достоверной.
Считается, что только показатели точности являются наиболее важными, но в то же время и наиболее трудными для нахождения критериями оценки и прогнозирования эффективности двигательных действий. Вопросы оценки точности и прогнозирования эффективности двигательных действий рассмотрены авторами ранее в работах [1, 5, 6].
Цель работы – разработка методики определения рейтинга спортсменов игровых видов спорта.
Методика определения рейтинга
Испытуемым предъявляли на экране видеомонитора окружность, на которой помещена метка 1 и точечный объект 2, движущийся с заданной скоростью по окружности, как показано на рис. 1.
Испытуемые, наблюдая за движением точечного объекта 2, в момент предполагаемого совпадения положения движущегося точечного объекта 2 с меткой 1 нажатием кнопки «Стоп» останавливали движение точечного объекта 2 по окружности. После останова компьютер вычислял ошибку не совпадения точечного объекта 2 и метки 1 – время ошибки запаздывания с положительным знаком, мс или упреждения с отрицательным знаком, мс и через заданное время, равное 1 секунде, возобновлял движение точечного объекта 2 по окружности.
Испытуемые выполняли описанную процедуру 13 раз, 3 начальных результата из анализа исключались, как принято в [5]. После этого определяли максимальное абсолютное значение Tmax ошибки несовпадения точечного объекта 2 и метки 1, мс; строили вариационный ряд ошибок несовпадения точечного объекта 2 и метки 1, вычисляли вариационный размах ряда по формуле:
R=tmax–tmin,
где tmax и tmin – соответственно наибольший и наименьший члены вариационного ряда, мс; вычисляли верхнюю квартиль максимального абсолютного значения Tmax ошибки несовпадения точечного объекта и метки, процент П абсолютных значений ошибок несовпадения точечного объекта и метки, находящихся в верхней квартили максимального абсолютного значения Tmax ошибки несовпадения точечного объекта и метки.
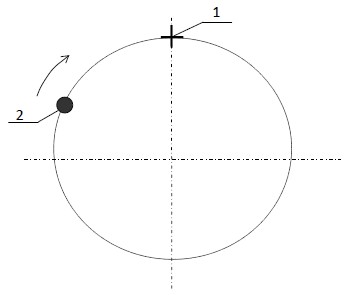
Рис. 1. Схема тестирования реакции на движущийся объект
Рейтинг Р вычисляли как обратную величину среднеарифметического значения максимального абсолютного значения Tmax ошибки несовпадения точечного объекта 2 и метки 1, вариационного размаха R и процента П абсолютных значений ошибок несовпадения точечного объекта 2 и метки 1, находящихся в верхней квартили максимального абсолютного значения Tmax ошибки несовпадения точечного объекта 2 и метки 1, умноженную на 100, по формуле [4]:
Р = 100× 1/(Тmax+R+П)/3 = 300/(Тр max+R+П)
|
Испытуемый |
Tmax, мс |
R, мс |
ВК |
% |
Р |
|
Б., 20 лет |
12 |
19 |
9,0 |
20 |
5,88 |
|
К., 23 года |
14 |
22 |
10,5 |
10 |
6,52 |
|
Д., 19 лет |
12 |
21 |
9,0 |
40 |
4,11 |
Tmax - максимальное абсолютное значение ошибки несовпадения точечного объекта и метки; R - вариационный размах значений ошибок несовпадения точечного объекта и метки; ВК - значение верхней квартили максимального абсолютного значения ошибки не совпадения точечного объекта и метки; % - процент абсолютных значений ошибок несовпадения точечного объекта и метки, находящихся в верхней квартили максимального абсолютного значения ошибки несовпадения точечного объекта и метки; Р – значение рейтинга.
Обсуждение
Анализ результатов тестирования свидетельствует, что максимальное абсолютное значение ошибки и вариационный размах ошибок не совпадения точечного объекта и метки у испытуемого К. несколько больше, чем у испытуемых Б. и Д. Однако процент абсолютных значений ошибок не совпадения точечного объекта и метки, находящихся в верхней квартили максимального абсолютного значения ошибки не совпадения точечного объекта и метки у испытуемого К. меньше, поэтому число его более точных реакций на движущийся объект и рейтинг выше, чем у испытуемых Б. и Д. По результатам тестирования испытуемый К. расценивается как наиболее перспективный и способный показать более высокие результаты в ответственных соревнованиях.
Успешность спортсмена в игровых видах спорта, как отмечается в [5], во многом зависит от пространственных (дифференцирование, точное воспроизведение и отмеривание пространственных интервалов, ориентация в пространстве) и временных (дифференцирование, точное воспроизведение и отмеривание временных интервалов) свойств.
Сложным пространственно-временным рефлексом является реакция на движущийся объект [6], поэтому этот тест может использоваться для определения рейтинга спортсмена игровых видов спорта путем оценки правильности принятия решений и точности двигательных действий.
Задача испытуемого, стремящегося остановить движущийся объект, точно совмещая его с меткой, состоит в нахождении некоторой величины упреждения с учетом скорости движения объекта, оставшегося расстояния и скорости своих двигательных действий. Действия испытуемого в подобной ситуации соответствуют действиям спортсмена игровых видов спорта, что позволяет оценить правильность принятия решений и точность двигательных действий испытуемого.
На современном этапе развития спорта возрастает необходимость эффективной рейтинговой оценки показателей подготовленности спортсмена для анализа и последующей корректировки как тренировочной, так и соревновательной деятельности. Обзор способов получения такой оценки по итогам соревновательной деятельности приведен в работе [9]. Так в футболе вычисляется показатель тактико-технических действий, для чего фиксируется темп их выполнения, время владения мячом, различные виды передач и процент брака. Это позволяет определить эффективность как отдельных футболистов, так и команды в целом.
В волейболе вычисляется интегральный показатель технико-тактического мастерства ПТМ спортсмена с учетом его амплуа по формуле:
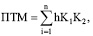
где n – количество приемов; h – эффективность приема; К1 – коэффициент специфичности приема; К2 – ценность приема.
В пляжном волейболе в качестве оценки используется коэффициент игровой подготовленности КИП, вычисляемый по формуле:
КИП= (а1+а2+а3+ … +аn)/n,
где а1, а2, а3, … , аn – оценка выполнения отдельных игровых действий; n – число игровых действий, выполняемых волейболистом.
В баскетболе за меру технического мастерства принимается математическое ожидание, а за технику выполнения М1 – средняя оценка, вычисляемая по формуле:
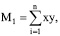
где n – количество приемов; x – вероятность выполнения приема; y – математическое ожидание оценки приема. Вероятность выполнения приема определяется по формуле:
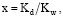
где Kd – количество выполнений одного приема; Kw – суммарное количество выполнений всех приемов.
В студенческом американском баскетболе вычисляется коэффициент полезности игрока КПИ, включающий большое количество показателей с весовыми коэффициентами, приведенных к игровому времени баскетболиста:
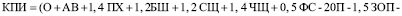
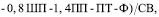
где О – набранные очки; АВ – атакующие передачи (всего); ПХ – перехваты; БШ – блокшоты; СЩ – подборы на своем щите; ЧЩ – подборы на чужом щите; ФС – фолы соперника на игроке; 2ОП – промахи 2-очковых бросков; 3ОП – промахи 3-очковых бросков; ШП – промахи штрафных бросков; ПП – потери при передачах; ПТ – потери технические; Ф – фолы игрока; СВ – сыгранное время.
А.Н. Корольков отмечает [3], что вопросы прогнозирования спортивных достижений являются постоянной темой многих исследовательских работ, в большинстве которых предпринимаются попытки предсказать будущие результаты путем экстраполяции временных рядов текущих результатов в зависимости от параметров тренировочных и соревновательных нагрузок на некоторый будущий момент времени. Для этого используются известные статистические методов анализа (факторный анализ, корреляция, регрессия и др.).
Так А.К. Тихомиров и соавт. [8] при обработке результатов тестирования вычисляют коэффициенты корреляции между этапными (ежегодными) значениями показателей. Н.М. Соколова и Э.А. Гайдуков считают [7], что построение линейных регрессионных моделей на основе результатов двигательных тестов, проводимых в каждый учебно-тренировочный месяц, в течение двух лет начального этапа тренировки юных легкоатлетов (мальчиков 10-12 лет), позволяет надежно прогнозировать результаты в ключевых характеристиках спринтерского бега и прыжков. Т. Е. Яворская [10] помимо линейной регрессии использует векторный и матричный анализ для выделения максимально возможного количества информативных параметров, дисперсионный и факторный анализ для решения задачи о минимально достаточном числе информативных параметров.
В последнее десятилетие возрос интерес к использованию нейронных сетей прежде всего для решения задач регрессионного анализа и анализа временных рядов с целью прогнозирования. Основная проблема использования нейронных сетей связана с нехваткой качественных данных, очищенных от ошибок и выбросов [2].
Заключение
Разработан метод определение рейтинга спортсмена игровых видов спорта по результатам тестирования реакции на движущийся объект. Он может быть использован как для первичного отбора, так для оценки качества тренированности и комплектации команды высококвалифицированных спортсменов.
Библиографическая ссылка
Полевщиков М.М., Роженцов В.В. ОПРЕДЕЛЕНИЕ РЕЙТИНГА СПОРТСМЕНА ИГРОВЫХ ВИДОВ СПОРТА // Международный журнал прикладных и фундаментальных исследований. 2015. № 9-1. С. 153-156;URL: https://applied-research.ru/ru/article/view?id=7459 (дата обращения: 09.02.2026).

