Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Медведев А.В. 1

---

1 Кемеровский филиал Российского экономического университета им. Г.В. Плеханова

В статье предложена математическая модель деятельности предприятия, решающая прямую задачу оптимального инвестиционного планирования в ее полной постановке: по заданному распределению стоимостей основных производственных фондов и стоимостей производимой на них продукции найти оптимальное распределение объемов инвестиций, производства продукции и финансирования инвестиционного проекта. Приведена краткая постановка задачи, описание и экономический смысл переменных, ограничений, критериев. Отличительной особенностью модели является возможность автоматического определения оптимальных объемов необходимых для реализации проекта инвестиционного и кредитного ресурса, что позволяет рассчитывать на решение ключевой для производителя задачи достижения состояния платежеспособности на всем горизонте планирования.

Статья в формате PDF

960 KB

линейная модель оптимизации

производственной предприятие

полная прямая задача инвестиционного планирования

1. Горбунов М.А. Оптимизационный пакет прикладных программ «Карма» и его применение в задачах бизнес-планирования / М.А. Горбунов, А.В. Медведев, П.Н. Победаш, А.В. Смольянинов // Фундаментальные исследования. 2015. №4. С. 42-47.

2. Медведев А.В. Моделирование стратегии социально-экономического развития региона на основе мезоэкономического подхода и оптимизационной математической модели // Вестник Красноярского госуниверситета. Серия «Физико-математические науки». 2006. №1. С.208-214.

3. Медведев А.В. Одна классификация прямых и обратных задач инвестиционного планирования / А.В. Медведев // Международный журнал прикладных и фундаментальных исследований. 2014. №10-2. С. 131а.

4. Медведев А.В., Победаш П.Н. Модель и оптимальный алгоритм согласования контракта между производителем, инвестором и поставщиком оборудования // Вестник Красноярского госуниверситета. 2006. №9. С.188-192.

5. Медведев А.В. Математическая модель оценки инвестиционной привлекательности региона / А.В. Медведев // Современные наукоемкие технологии. 2013. №8-2. С.357-361.

6. Моделирование производственно-инвестиционной деятельности фирмы / Под ред. Г.В. Виноградова. М.: ЮНИТИ-ДАНА, 2002. 319 с.

7. Никитенко С.М. Методологические и методические аспекты преобразования технологии в инновационный продукт / С.М. Никитенко, А.В. Медведев, А.В. Гребенников // Инновации. 2013. №6(176). С.115-119.

В настоящее время в сфере моделирования деятельности производственного предприятия и оценки ее экономической эффективности наблюдается недостаток моделей, с одной стороны, описывающих основные составляющие такой деятельности, а с другой, – позволяющих осуществить эффективную автоматизированную обработку получаемой из модели информации. Последнее требование обуславливает применение статических моделей, позволяющих учесть большее количество особенностей, необходимых для бизнес-планирования деятельности предприятия.

В работах [2,4] показано, что при планировании деятельности производственных предприятий целесообразно использовать линейные, оптимизационные модели, в которых, с достаточной для целей бизнес-планирования подробностью, описаны инвестиционная, операционная и финансовая составляющие. Пусть далее деятельность производителя продукции n видов (товаров и/или услуг) описывается, выраженными в стоимостном виде, материальными и финансовыми потоками стратегического (прибыль, инвестиции) и тактического (выручка от продажи продукции, амортизация, фонд оплаты труда, налоги, оборотные затраты, кредиты, дотации и пр.) характера. Важной предпосылкой здесь является выполнение принципа чистых отраслей: на одном типе ОПФ производится один вид продукции. Кроме того, предполагается, что указанная деятельность делится на три составляющие [6]: инвестиционную (учет потоков, обусловленных приобретением (продажей) основных производственных фондов (ОПФ), операционную (учет выручки, затрат на амортизацию ОПФ, оплату труда, сырья и материалов, энергии и т.п.) и финансовую (учет кредитов, налогов, сборов, дотаций и других доходно-расходных потоков, обеспечивающих финансирование (платежеспособность) производителя). Рассмотрим также такой инновационный аспект деятельности предприятия, как наличие периода послепродажного обслуживания инновационной, высокотехнологичной продукции [7], равного горизонту планирования Т. Требуется определить в стоимостном виде оптимальные объемы приобретаемых ОПФ (инвестиций), выпуска продукции каждого вида, кредитов, дотаций, при которых дисконтированное сальдо доходов и расходов, а также дисконтированный налоговый поток за горизонт планирования T являются максимальными с учетом естественных ограничений деятельности двух экономических агентов – производителя и управляющего налогового органа.

Введем далее следующие обозначения:

n – количество видов продукции, ед.;

k=1,…,n – порядковый номер ОПФ;

m_k – количество единиц k-го ОПФ, ед.ОПФ;

с_k – стоимость единицы k-го ОПФ, ден.ед/ед.ОПФ;

P_k – стоимость продажи единицы продукции на k-го вида, ден.ед./ед.продукции;

V_k – производительность k-го ОПФ за период Т, ед.продукции/(ед. ОПФ);

T_k – время полезного использования k-го ОПФ, лет;

q_k – спрос на продукцию, произведенную на k-м ОПФ, за период Т ден.ед./(ед.прод);

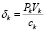– максимальная фондоотдача k-го ОПФ за период Т, %;

α_i, i=1,…,4 – соответственно ставки налогов на добавленную стоимость, имущество, прибыль, страховых взносов в социальные фонды;

α₅ – ставка других, зависящих от объемов производства, налоговых или неналоговых затрат;

p – доля оборотных затрат в сумме всех затрат производителя (экспертный показатель материалоемкости производства);

β – доля выручки от продаж, выделяемая в фонд оплаты труда (ФОТ) (экспертный показатель трудоемкости производства);

Т – горизонт планирования, rps(k)=Rs/Rp – экспертно задаваемый коэффициент, отражающий, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж инновационной продукции k-го вида за период Т. Следует отметить, что трактовка указанного коэффициента здесь отличается от трактовки аналогичного ему в моделях, представленных, например, в работах [5,7], что приводит к некоторым, несущественным для содержательного смысла, отличиям соответствующих математических моделей.

Введем далее следующие обозначения:

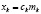(k=1,…,n) – стоимость всех приобретаемых ОПФ k-го вида за период Т, ден.ед.;

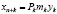(k=1,…,n) – выручка от реализации всей продукции k-го вида за период Т (в количестве y_k (ед.продукции/(ед.ОПФ), стоимостью P_k (ден.ед./ед.прод.)), произведенной на k-м ОПФ, ден.ед.;

x_2n+1=Cr – сумма кредита, взятого под обеспечение финансирования бизнес-проекта;

x_2n+2=Dot – сумма дотаций предприятию за период Т.

Тогда, учитывая введенные обозначения, получим:

W_int= R_int –Z – прибыль предприятия за период Т, ден.ед.;

где

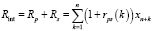– сум ма выручки от продаж продукции k-го вида и ее сервисного обслуживания за период Т, ден.ед.;

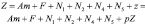– общие затраты производителя за период Т, ден.ед.;

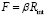– суммарные амортизационные отчисления за период Т, ден.ед.;

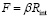– общий ФОТ за период Т, ден.ед.;

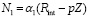– налог на добавленную стоимость;

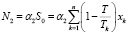– налог на имущество;

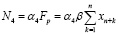– страховые взносы;

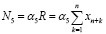– другие нало говые и неналоговые затраты (например, налог на добычу полезных ископаемых, экологические штрафы, «откаты» и пр.), зависящие от объемов производства;

z – материальные (сырье, материалы и пр.) затраты предприятия (в предлагаемой модели оцениваются экспертно через сумму всех затрат) за период Т.

Пусть предприятие (производитель) для финансирования своей деятельности предполагает взять кредит в сумме Cr на Тс лет под rс процентов годовых. В этом случае ежегодный платеж (основной долг плюс проценты) по кредиту составит:

S_пл=Cr(1+ r_с(12Т_с+1)/24)= Cr+[r_с(12Т_с+1)/24]Cr = Cr+ψCr.

Тогда, в предположении, что основной долг по кредиту преимущественно тратится на приобретение необходимого количества ОПФ (инвестиции в ОПФ), критерий производителя за период Т можно записать в виде:

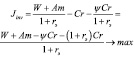
– чистая дисконтированная стоимость собственных средств организации, ден.ед.,

где 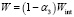– чистая прибыль, ден.ед.,

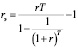– эффективная ставка дис контирования проекта за период Т.

С учетом введенных обозначений, математическая модель, описывающая деятельность производственного предприятия, принимает следующий вид двухкритериальной задачи линейного программирования (ЗЛП):

;

;

;

;

;

,, ,

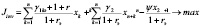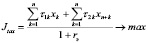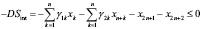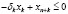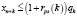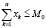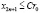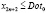где

,

,

,

.

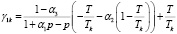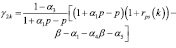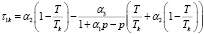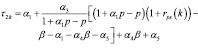M₀ – максимальная сумма инвестиций в ОПФ,

Cr₀ – максимальная сумма кредита,

Dot₀ – максимальная сумма дотаций.

Здесь первые два соотношения представляют собой критерии производителя и налогового центра соответственно, содержательно отражающие чистый дисконтированный доход указанных экономических агентов. Первое неравенство отражает условие платежеспособности производителя, использующего для реализации бизнес-проекта как внутренние (прибыль), так и внешние (кредиты и дотации) источники. Второе и третье неравенства выражают естественные для всякого бизнес-проекта ограничения на объемы производства, связанные с ограниченностью фондоотдачи ОПФ и спроса на продукцию. Последняя группа неравенств отражает ограниченность имеющихся в распоряжении производителя объемов финансовых ресурсов.

Имеется следующая трактовка критерия модели и суммы собственных средств производителя. Кредит в размере Cr расширяет финансовые возможности (платежеспособность) производителя и, тем самым, допустимое множество задачи (1), описываемое неравенством DSint≥0. Вместе с тем, кредит является платным финансовым ресурсом стоимостью в размере уплачиваемых за него процентов. Это учитывается в критерии производителя путем вычитания суммы процентных платежей. Включение переменной x2n+1 в модель позволяет решить важную для производителя задачу определения оптимального объема заемного ресурса, необходимого для достижения состояния платежеспособности на всем горизонте планирования своей деятельности.

Модель (1) позволяет находить оптимальные распределения инвестиций по видам ОПФ, объемы производимой на них продукции, а также оптимальные значения внешних источников финансирования – кредитов и дотаций – с точки зрения максимизации чистой приведенной стоимости производственного предприятия. Кроме того, указанная модель позволяет осуществлять двухкритериальный анализ при взаимодействии предприятия с налоговым центром c использованием оптимизационного пакета, подробно описанного, например, в работе [1].

Модель (1) представляет собой линейную задачу оптимального управления, учитывающую все основные виды деятельности производственного предприятия – инвестиционную, операционную и финансовую, что позволяет решить прямую задачу оптимального инвестиционного планирования [3] в ее полной постановке: по заданному распределению стоимостей ОПФ и стоимостей производимой на них продукции найти оптимальное распределение инвестиций, объемы производства продукции и объемы необходимого для обеспечения платежеспособности экономического субъекта финансового ресурса.

Библиографическая ссылка