Интенсивное изучение электродинамических явлений, возникающих в периодических решетках различной конструкции, ведущееся последние несколько десятилетий, традиционно связано с потребностями практики. Исследование свойств одномерных дифракционных решеток привело к созданию на их основе различных частотных и поляризационных фильтров, антенн, резонаторов, преобразователей излучения и иных устройств, широко используемых в СВЧ и оптическом диапазонах [1, 2]. В последние годы наблюдается рост интереса к изучению свойств двух- и трехмерных диэлектрических периодических структур, вызванный появлением нового класса оптических материалов – фотонных кристаллов, с которыми принято связывать возможные революционные события в технике связи и компьютерных технологиях [3].
К настоящему времени установлен ряд свойств, присущих только дифракционным решеткам различной геометрии, к числу которых можно отнести эффекты резонансного отражения и прохождения волн через такие структуры, наличие запрещенных и разрешенных зон в спектре собственных электромагнитных состояний решеток, аномалии Вуда и т.д. Одно из интереснейших явлений, наблюдающееся при падении плоской волны на одномерную бесконечно протяженную дифракционную решетку из идеально проводящих цилиндров произвольного поперечного сечения, заключается в полном (без отражения) прохождении волны сквозь структуру при выполнении условия (рис. 1):
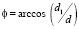(1)
где d1 – минимальное расстояние между соседними элементами решетки, d – период структуры, φ – угол падения, отсчитываемый от нормали к плоскости решетки.
Данный эффект наблюдается только для Н – поляризованных волн (вектор напряженности магнитного поля параллелен осям проводников) в частых решетках (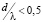
, где λ – длина волны) и по физическому механизму близок, по-видимому, к эффекту Брюстера, имеющему место при определенных условиях на границе раздела сплошных сред. Эффект полного прохождения волн через дифракционную структуру впервые был обнаружен Г.Д. Малюжинцем в конце 30-х годов прошлого века, и подробно исследовался в [2, 4]. Целью настоящей работы является теоретическое и экспериментальное изучение возможности возникновения аналогичных эффектов при облучении локальными источниками плоских и многослойных дифракционных решеток конечной протяженности.
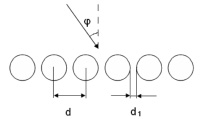
Рис. 1. Одномерно-периодическая дифракционная решетка
Экспериментальные результаты
Экспериментальная часть исследований проводилась с применением комплекта аппаратуры Р2-65, предназначенной для измерений ослабления поля в волноводных трактах и адаптированной для изучения дифракции волн на открытых системах. В качестве передающей и приемной антенн использовались волноводные излучатели. В ходе измерений расстояние между ними оставалось неизменным и составляло 35 см. Эксперименты проводились на частоте 32 ГГц. Погрешность определения уровня поля не превышала 0,5 дБ.
Дифракционная решетка представляла собой систему периодически установленных цилиндрических металлических элементов кругового поперечного сечения. Высота элементов составляла 30 см, что практически полностью исключало влияние конечности длины цилиндров на результаты измерений. Период решетки равнялся 3,5 мм, диаметр элементов структуры – 2,6 мм. В процессе измерений решетка вращалась таким образом, что ее плоскость изменяла свою ориентацию относительно линии связи излучатель – приемник в диапазоне от 0 до 90 градусов, при этом центральный элемент структуры занимал неизменную позицию относительно антенн. Точность угла установки решетки составляла 1 °.
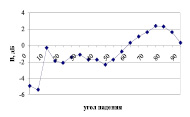
Поскольку непосредственное определение коэффициентов отражения и прохождения падающей на структуру волны при данной постановке эксперимента не представлялось возможным, в ходе измерений определялся относительный уровень поля, прошедшего сквозь решетку, который характеризовался величиной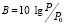 
, где Р – мощность излучения в присутствии решетки, Р0 – мощность, определяемая при отсутствии дифракционной структуры при том же пространственном разносе антенн. Полученные результаты представлены на рис. 2–4 в виде угловых зависимостей поля. Соответствующие углы определялись взаимной ориентацией плоскости решетки и линии связи антенн таким образом, что при нормальном падении волны на структуру угол считался равным нулю градусов. На рис. 2, а представлены результаты, относящиеся к однорядной дифракционной решетке, состоящей из 21 элемента. Рис. 2, б и 2, в описывают угловые зависимости поля прошедшего через аналогичные двух- и трехрядные структуры. Расстояние между рядами элементов в таких решетках равнялось периоду расположения цилиндров.
Из графиков следует, что эффект Малюжинца, выражающийся в данном случае в относительном увеличении уровня поля в секторе углов от 60 до 80 градусов на всех полученных зависимостях, может наблюдаться как в плоских, так и в объемных дифракционных решетках конечной протяженности. Оценка условия проявления эффекта Малюжинца, выполненная по формуле (1) для вышеуказанных параметров структуры, дает величину 75,1 °, что соответствует полученным результатам. Небольшое смещение максимума в угловых зависимостях поля, прошедшего через объемные структуры, в сторону меньших углов может быть объяснено взаимным влиянием рядов решеток.
Численное моделирование и обсуждение результатов
Теоретическое описание возбуждения дифракционных структур локальным источником проводилось по методике, изложенной в [5]. Поскольку рассматривалось взаимодействие излучения с системой бесконечно протяженных элементов, а линия связи антенн располагалась в плоскости, ортогональной осям цилиндров, решалась двумерная задача. При этом обе антенны описывались как элементарные магнитные излучатели, в экваториальной плоскости которых и проводился анализ дифракционной картины (рис. 3).
а) б)
в)
Рис. 2. Измеренный относительный уровень поля, прошедшего через дифракционную структуру, в зависимости от угла падения волны: а) для однорядной решетки; б) для двухрядной; в) для трехрядной
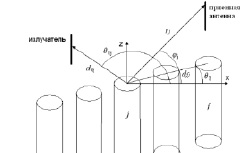
Рис. 3. К решению задачи о возбуждении системы цилиндров
Поле в данном случае было удобно описывать с помощью магнитного вектора Герца, единственная ненулевая z-ая компонента которого может быть представлена в виде:
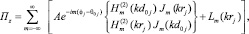(2)
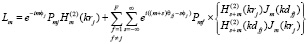. (3)
Здесь А – амплитудный коэффициент,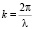 
– волновое число, 
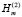– функция Ханкеля второго рода m – го порядка, Jm – функция Бесселя m – го порядка, F – общее число элементов в структуре, Pm – неизвестные коэффициенты, характеризующие амплитуду и фазу возбуждения цилиндров и определяемые из граничных условий. Остальные обозначения представлены на рис. 5. Первое слагаемое в выражении (2) описывает первичное поле, создаваемое источником излучения, второе – определяемое в соответствии с (3) – поле, переизлученное элементами дифракционной решетки. В свою очередь, в выражении (3) первое слагаемое характеризует рассеяние волн на произвольном j – ом элементе, второе слагаемое описывает поле, переотраженное всеми остальными цилиндрами, выраженное через волновые функции j – ого цилиндра путем применения теоремы сложения для цилиндрических функций.
Из удовлетворения граничным условиям на поверхности каждого входящего в решетку идеально проводящего элемента (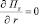
при rj = a, где a – радиус цилиндра) строится система F неоднородных линейных алгебраических уравнений относительно Pm, определяя которые, получаем строгое решение поставленной задачи.
Следует отметить, что описанная методика не налагает ограничений на взаимное положение антенн и дифракционных элементов и может быть использована для описания процессов возбуждения как периодических решеток, так и структур с произвольным расположением рассеивателей. Однако недостатком данного подхода являются высокие требования к вычислительным ресурсам и значительное время счета, особенно в случае, если поперечные размеры цилиндров, образующих структуру, оказываются соизмеримы с длиной волны излучения, следствием чего является необходимость учета большого числа членов в рядах (2) и (3). Поэтому в рамках численного моделирования, проводимого в данной работе, рассматривалась дифракция волн только на одно- и двухрядных решетках. В результате расчетов вновь, как и в экспериментах, определялись угловые зависимости относительного уровня поля, прошедшего сквозь структуры.
а) б)
Рис. 4. Результаты численного моделирования относительного уровня поля в звисимости от угла падения волны: а) для однорядной структуры; б) для двухрядной
На рис. 4, а представлены результаты, относящиеся к однорядной решетке, состоящей из 21 элемента, на рис. 4, б – к аналогичной двухрядной структуре. Остальные параметры моделирования полностью соответствовали условиям проведения экспериментальных исследований. На полученных зависимостях вновь видны интервалы углов, в пределах которых поле, прошедшее сквозь решетку, оказывается усиленным по сравнению с полем в свободном пространстве, что дает основание говорить о проявлении эффекта Малюжинца в рассматриваемых структурах.
Заключение
Таким образом, в настоящей работе теоретически и экспериментально доказана возможность возникновения эффекта полного прохождения Н – поляризованных волн сквозь частые дифракционные решетки – эффекта Малюжинца – в случае возбуждения объемных (многослойных) структур конечной протяженности.
Автор благодарен Басанову Б.В. за помощь в проведении экспериментов.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 15-47-04315).
Библиографическая ссылка
Ветлужский А.Ю. ПОЛНОЕ ПРОХОЖДЕНИЕ ИЗЛУЧЕНИЯ ЧЕРЕЗ МНОГОСЛОЙНЫЕ ДИФРАКЦИОННЫЕ СТРУКТУРЫ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 10-4. – С. 611-614;URL: https://applied-research.ru/ru/article/view?id=7591 (дата обращения: 23.11.2024).