Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Повзнер А.А. 1 Ясюлевич И.А. 1 Филанович А.Н. 1

---

1 ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина»

Твердые растворы Fe1-xCoxSi являются важными прототипами спинтронных материалов, так как обладают хорошей технологической совместимостью с кремнием. В последнее время исследование их физических свойств возобновилось с новой силой из-за открытия новых интересных фактов, таких как связь кристаллографической и спиновой киральности. В настоящей работе был выполнен первопринципный расчет электронной структуры по схеме LDA+U (в методе FP-LAPW) без спиновой разбалансировки в пакете Elk, с использованием экспериментальных данных о кристаллической структуре для разных концентраций твердого раствора Fe1-xCoxSi. Первопринципный расчет плотностей электронных состояний Fe1-xCoxSi выполнен для концентраций х = 0,1, 0,3, 0,5. Проведен анализ плотностей электронных состояний. Рассмотрено изменение фактора стонеровского усиления для различных составов Fe1-xCoxSi. В результате выполненной работы получено, что при переходе от кристаллографически правых образцов к кристаллографически левым качественное изменение плотности электронных состояний не происходит.

Статья в формате PDF

2269 KB

электронная структура

LDA

FP-LAPW

плотность состояний

киральность

FeCoSi

1. Изюмов Ю.А., Анисимов В.И. Электронная структура соединений с сильными корреляциями. – М.: НИЦ «РХД», 2003. – C. 376.

2. Повзнер А.А., Волков А.Г., Филанович А.Н. Электронная структура и магнитная восприимчивость почти магнитных металлов (на примере палладия и платины) // ФТТ. – 2010. – Т. 52. – Вып. 2. – С. 1879–1884.

3. Asanabe S., Shinoda D., Sasaki Y. Semimetallic properties of Co1-xFexSi solid solutions. – Phys. Rev. A. 1964, Vol.134. P. 774.

4. Beille J., Bloch D., Jaccarino V., Wernick J.H., Wertheim G.K. Effects of hydrostatic pressure on the magnetic properties of disorder monosilicide FexCo1-xSi alloys // J. de Physique. – 1997. –Vol. 38. – P. 339.

5. Beille J., Bloch D., Towfiq F., Voiron J. The magnetic properties of FexCo1-xSi and FexCo1-xTi alloys // J. Magnet. And Magnet. Mater. – 1979. – Vol. 10. – P. 265.

6. Grigoriev S.V., Chernyshov D., Dyadkin V.A., Dmitriev V., Maleyev S.V., Moskvin E.V., Menzel D., Schoenes J., and Eckerlebe H. Crystal Handedness and Spin Helix Chirality in Fe1-xCoxSi // Phys. Rev. Lett. – 2009. – Vol. 102. – P. 037204.

7. Mazurenko V.V., Shorikov A.O., Lukoyanov A.V., Kharlov K., Gorelov E., Lichtenstein A.I., Anisimov V.I. Metal-insulator transition and magnetism in correlated band insulator: FeSi and Fe1-xCoxSi // Phys. Rev. B. – 2010. – Vol. 81. – P. 125131.

8. Perdew J.P. and Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy // Phys. Rev. B. – 1992. –Vol. 45. – P. 13244.

9. Urasaki K., Saso T. Thermal and dynamical properties of the two-band Hubbard model compared with FeSi // Phys. Rev. B. – 1998. – Vol. 58. –P. 15528.

10. Zhi-Hui H., Wei H., Young S. and Zhao-Hua C. First principles study on the electronic structure and magnetism of Fe1-xCoxSi alloys // Chin. Phys. Soc. – 2007. – Vol. 16. – P. 3863.

Методом рассеяния поляризованных нейтронов [8] было показано что спиновые спирали в кубических магнетиках Fe1-xCoxSi могут быть реализованы как в правой, так и в левой конфигурациях киральной симметрии для различных концентраций структуры Fe1-xCoxSi вдоль оси (111) для кобальта. В исследовании [6] демонстрируется, что для Fe1-xCoxSi спиновая киральность обратна кристаллографической киральности. Что бы выяснить как связана спиновая и кристаллографическая киральность необходимо прежде всего изучить электронную структуру Fe1-xCoxSi. Электронная структура Fe1-xCoxSi описывалась ранее в работах [7, 10] она рассчитывалась в методе LSDA (FP-LAPW) со спиновой разбалансировкой. В данных расчетах за основное состояние брался слабый ферромагнетизм, что не соответствует экспериментально наблюдаемой геликоидальной структуре, кроме того в области парамагнитных температур эти результаты неприменимы.

Причина, по которой следует отказаться от LSDA в пользу LDA+U в том, что в DFT одноэлектронный потенциал действует одинаково на состояния заполненных и пустых орбиталей. Это приводит к тому, что частично заполненная t2g – зона с направлением спина «вниз» для Fe1-xCoxSi остается металлической в LSDA. Применение метода LDA+U радикально меняет результат. Орбитально-зависимый потенциал дает расщепление энергий заполненных и пустых d-состояний примерно на величину среднего кулоновского взаимодействия U. Пустые eg↓ – состояний поднимаются по энергии вверх, в то время как заполненные состояния сдвигаются вниз [1].

В настоящей работе расчеты электронной структуры выполнены по схеме LDA+U (в методе FP-LAPW) без спиновой разбалансировки в пакете Elk. Уровень Ферми находится в нуле энергии. Использовались экспериментальные данные [6] о кристаллической структуре, согласно которым Fe1-xCoxSi обладает группой симметрии Р213 и восьмью атомами в элементарной ячейке. Параметры решетки, применяемые в наших расчетах, были заимствованы из экспериментальных работ [3].

Расчет проводился при параметре U = 1eV [9] с учетом спин орбитального взаимодействия. Значение JH = 0,49 эВ было определено в рамках метода, предложенного в, который базируется на использовании потенциала Юкавы и эффективной длины экранирования. Использовался обменно-корреляционный потенциал LDA [8]. Каждый из наших расчетов был выполнен на 16х16х16 k-сетке, маффин-тин радиусы RFe(Co) = 2,4 a.u., RSi = 2,2 a.u. Параметр обрезания, дающий число плоских волн в межузельной области принимался Rmt*Kmax = 7, где Kmax максимальное значение вектора обратной решетки, используемого в разложении плоских волн в этой зоне. Критерии сходимости, которые мы использовали: изменение эффективного потенциала, а так же изменение полной энергии на последующих итерациях должны были быть меньше чем 0.000001 Ha и 0.0001 Ha соответственно. Изменение концентрации кобальта в Fe1-xCoxSi учитывалось с помощью параметра «chgexs», который контролирует количество заряда в элементарной ячейке. В нашем случае с помощью этого параметра каждому атому железа придавался дополнительный заряд, чтобы учесть концентрацию легирующего элемента (кобальта). Нейтральность заряда в ячейке сохранялась во всех расчётах.

Координаты атомов Fe, Co и Si применяемые для расчета разных энантиоморфных форм Fe1-xCoxSi:

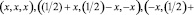
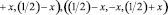(1)

где х принимает соответственно значения xFe(Co) = 0,8632 и xSi = 0,1574 для правой формы, xFe(Co) = 0,1376 и xSi = 0,8426 для левой формы (левая форма соответствует замене х на разность 1-x) [6].

Полученная плотность электронных состояний при х = 0,1 качественно согласуются с данными [7], в частности имеем узкую щель около 0,1eV. Для составов с х = 0,3 и 0,5 расчеты ранее не проводились.

Обе родительские системы, как известно, являются немагнитными. FeSi парамагнитный полупроводник с узкой зонной щелью, а CoSi диамагнитный полуметалл. DOS FeSi и CoSi очень похожи, разница – в жестком сдвиге EF. В Случае FeSi EF лежит в щели в середине d зоны демонстрируя высокую плотность состояний вблизи границ щели. Наоборот EF в CoSi лежит в энергетической области где DOS является очень низкой что является характерным для полуметалла. Твердые растворы этих соединений так же имеют B20 кристаллическую структуру, расположение уровня Ферми в этих растворах соответствует промежуточному значению их родительских систем и коррелирует с изменением концентрации Co, о чем свидетельствуют наши данные. Для широкой области концентраций (0,05 < х < 0,8) Fe1-xCoxSi сплавы являются металлическими и имеют геликоидальную магнитную структуру с большим вектором спирали 10–100нм [6].

В выполненных расчетах при изменении концентрации Fe1-xCoxSi, а следовательно так же спиновой и кристаллографической киральности, изменяется не только положение уровня Ферми но и ширина щели от 0,086 eV до 0,156 eV, что указывает на то что при данных концентрация Fe1-xCoxSi остается узкозонным полупроводником. В результате расчёта плотностей электронных состояний Fe1-xCoxSi для разных концентраций x, скачкообразного изменения плотности электронных состояний при переходе от кристаллографически правых образцов при концентрациях x = 0,1 к кристаллографически левым при концентрациях x = 0,3, 0,5 не выявлено.

Очень важным параметром является фактор S стонеровского усиления 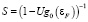[2]

. (2)

Учитывая, что в рамках теории Стонера:

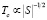(3)

можно оценить зависимость температуры Кюри от концентрации и сравнить полученную зависимость с экспериментальными данными [4, 5]. Для рассматриваемых составов фактор Стонера равен 0,99, 0,972, 1,22 соответственно. В результате получаем согласие с экспериментом для концентраций x = 0,1, 0,3, что подтверждает правильность расчета плотностей электронных состояний для разных концентраций Fe1-xCoxSi. В тоже время имеем расхождение с экспериментальными данными для концентрации x = 0,5.

Далее нами был проведен расчет левой формы Fe0.9Co0.1Si (в работе [6] указывается, что для такой концентрации x методом рассеяния поляризованных нейтронов было установлено, что существует только правая форма). Проанализировав плотности электронных состояний для данной концентрации x для левой и правой формы мы пришли к выводу, что в расчетах по схеме LDA+U (в методе FP-LAPW) в пакете Elk плотности электронных состояний не значительно отличаются друг от друга (различаются только в окрестностях 2 пиков удаленных на большой энергетический интервал от уровня Ферми).

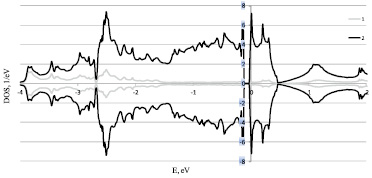
Рис. 1. Расчет плотностей электронных состояний правой формы Fe0,9Co0,1Si 1 – s+p и 2 – d электронов в рамках LDA+U

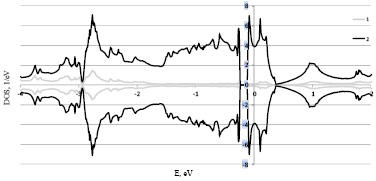
Рис. 2. Расчет плотностей электронных состояний левой формы Fe0,7Co0,3Si 1 – s+p и 2 – d электронов в рамках LDA+U

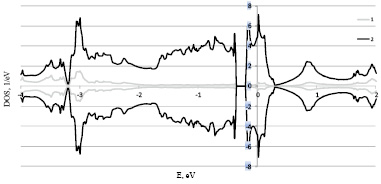
Рис. 3. Расчет плотностей электронных состояний левой формы Fe0.5Co0.5Si 1 – s+p и 2 – d электронов в рамках LDA+U

В работе [6] представлены интересные результаты о спиновой киральности Fe1-xCoxSi, в частности показано, что в Fe1-xCoxSi спираль переходит от лево-вращающейся при концентрациях x = 0,1, 0,15 к право-вращающейся при концентрациях x = 0,2, 0,25, 0,3, 0,5, при этом образцы переходят из кристаллографически правых образцов к кристаллографически левым при тех же концентрациях, что указывает на связь спиновой и кристаллографической киральности. Однако проведенный анализ плотностей состояний Fe1-xCoxSi для концентраций x = 0,1 для левой и правой формы показывает, что они отличаются не значительно, а при переходе от кристаллографически правых образцов x = 0,1 к кристаллографически левым x = 0,3, 0,5 качественное изменение плотности электронных состояний не происходит. Полученные значения температур Кюри соответствуют экспериментальным, только для концентраций x < 0,5. Однако дальнейшее исследование электронных и магнитных свойств Fe1-xCoxSi в любом случае требует учета спин-флуктуационных эффектов, а также кирального взаимодействия, приводящего к возникновению геликоидального ферромагнетизма.

Библиографическая ссылка