В современном информационном обществе полноценно реализовать себя, быть успешными могут люди, не просто обладающие системой предметных знаний, а интеллектуально развитые личности, свободно ориентирующиеся в быстро меняющемся мире, умеющие самостоятельно принимать ответственные решения в ситуации множественности выбора, анализировать причины и прогнозировать возможные последствия тех или иных событий и явлений, способные находить инновационные решения в условиях неопределенности, преодолевать консерватизм и отличающиеся мобильностью, динамизмом, конструктивностью. Всё это требует развития такого важного интеллектуального качества как гибкость мышления. Одним из эффективных средств развития данного качества мышления можно считать обращение математической задачи.
Под обращением математической задачи следует понимать последовательное видоизменение её путём извлечения из условия части или даже всех данных и включения их в требование; при этом из него, соответственно, исключаются несколько или все найденные искомые и переводятся в условие; обращённая задача станет обратной по отношению к исходной, если все её требования и условия полностью поменяются местами [1, 2].
Поскольку обращённые задачи, как уже говорилось, получаются в результате своеобразного оборота (обращения) элементов условия и требования исходной задачи, то для отражения этих изменений можно ввести специальную характеристику – меру обращённости задачи. Для её выражения обозначим число элементов условия исходной задачи через Nд, а число искомых в её требовании через Nи, число данных, перешедших после процесса обращения задачи в её требование, примем за N’д, а число искомых, включенных в её условие, - за N’и, тогда меру обращённости задачи (обозначим её буквой m) можно условно выразить формулой:
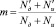∙100 %.
Очевидно, мера обращённости будет максимальна у обратной задачи и она равна 100 %. Собственно говоря, мера обращённости, введённая таким образом, позволяет ранжировать вновь полученные задачи по степени их обращения. Так, если прямая задача обращена полностью, то мера обращённости полученной задачи будет, как уже отмечалось выше, равна 100 %, если же имело место частичное обращение исходной задачи, то мера обращённости будет меньше 100 %. Диапазон варьирования меры обращённости определяется промежутком 0 < m ≤ 100 % .Понятно, что введённая таким образом мера обращённости является внешней характеристикой, показывающей величину «оборота» структурных элементов исходной задачи, и мало что даёт в оценке тех перемен в задачной ситуации, которые связаны с внутренними процессами, происходящими при её решении. Для отражения развивающей ценности обращения задач нужна характеристика, показывающая изменения в мыслительных процессах школьников. Так, для оценки обращения как средства, развивающего гибкость мышления, таким показателем может выступать число изменений хода мысли на обратный по сравнению с тем, который имел место при решении исходной задачи. Такие изменения могут быть связаны, например, с использованием в решениях взаимно обратных мыслительных операций, математических действий, видов математической деятельности. Если, к примеру, при решении прямой задачи по значениям двух слагаемых определялось значение их суммы, а при решении обращённой задачи по значению суммы и одного из слагаемых находилось значение другого слагаемого, то можно констатировать, что произошло изменение хода мысли с прямого на обратный.
В школьном курсе математики изучается немало взаимно обратных действий арифметического, алгебраического, логического характера: сложение и вычитание, умножение и деление, возведение в степень и извлечение корня, логарифмирование и потенцирование, нахождение корней уравнения и составление уравнения по значениям его корней, раскрытие скобок и заключение в скобки, дифференцирование и интегрирование и т.д. Взаимосвязь обратных действий выражается в том, что они показывают две различные стороны одно и того же процесса. Они существуют в синтезе, взаимно дополняя друг друга.
Характеристику обращения, показывающую изменения внутренней структуры задачи, связанные с переключением с прямого хода мысли на обратный в решениях исходной и обращённой задачи, логично назвать мерой обратимости. Для её численного выражения, обозначим за N′п/о – реальное количество изменений с прямого хода мысли на обратный в решениях исходной и обращённой задачи, а за Nп/о – возможное количество изменений хода мысли с прямого на обратный. Тогда математически меру обратимости задачи (обозначим её буквой М) можно записать так:
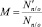∙100 %.
Причём стоит отметить, что у одной и той же задачи мера обратимости может быть различной, поскольку любую задачу возможно решить несколькими способами и произойдёт ли изменение хода мысли с прямого хода на обратный зависит от того, каким способом решена обращённая задача.
Обращаем внимание на то, что мера обращённости задачи это количественная характеристика процесса обращения, связанная с изменениями внешней структуры исходной задачи, а мера обратимости – качественная характеристика, выявляемая посредством сопоставления внутренних структур прямой и обращённой задач.
Ещё одной важной характеристикой обращения задачи можно считать потенциал обращения задачи P, показывающий максимально возможное количество обращений исходной задачи. Возникает вопрос, а допустимо ли, не осуществляя непосредственно процесс обращения какой-либо задачи, просчитать возможное количество её обращений? Если да, то как это сделать? Замечаем, что количество обращений задачи зависит от числа данных {yi} условия У исходной задачи и числа её искомых {tj} требования Т. Как было показано, процесс обращения задачи строится на всевозможных комбинациях элементов yi условия У задачи, переходящих в её требование Т, и различных комбинациях элементов tj требования исходной задачи, поступающих в её условие У.
Вычислим, сколько различных кортежей можно составить из элементов двух множеств У и Т таким образом, чтобы в кортеже было хотя бы по одному элементу от каждого множества У, Т, причём порядок их расположения нам не важен, отметим, что У = {y1, y2, y3… yn}, Т = {t1, t2, t3… tk}, где k, n є N.
Так, выбрать один элемент уi, т.е. одно произвольное условие из множества У возможно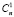 
способами, соответственно два элемента уi – 
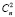способами и т.д.
1 элемент уi …………………………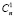 
способами;
2 элемента уi………………………...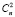
способами;
3 элемента уi…………………..……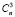
способами;
……………………………………………
n элементов ………………………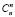
способами.
По свойству сочетаний сумма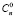 
+ 
+ 
+ 
+…+ 
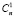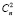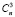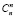= 2n, исключая тот случай, когда не выбран ни один элемент 
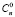= 1, получим, что общее число способов выбора кортежей элементов уi из множества У равно: 
+ 
+ 
+…+ 
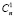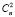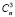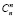= 2n – 1.
Рассуждая аналогичным образом над выбором кортежей, состоящих из различных комбинаций элементов tj множества Т, получим, что общее число способов их выбора равно:
+ 
+ 
+…+ 
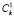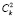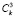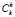= 2k – 1, исключая опять же случай, когда не выбран ни один элемент. В итоге, комбинацию элементов из множества У мы можем выбрать 2n –1 способами, и при любом выборе комбинации {yi} элементов У комбинацию {tj} элементов множества T можем выбрать 2k – 1 способами, тогда по правилу умножения, комбинацию из элементов данных и требований (т.е. множеств У и Т) можно выбрать (2n – 1)∙(2k – 1) способами. Таким образом, потенциал обращения любой задачи определяется по формуле:
P = (2n – 1)∙(2k – 1),
где n – число данных задачи, k – число её искомых.
Поскольку реально не все обращённые задачи получаются корректно поставленными, то считаем необходимой ещё одну характеристику – продуктивность обращения задачи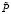 
, отражающую меру полезности использования этой задачи с целью получения обращённых задач. Для её определения используем формулу:
= 
,
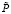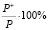где P+ – количество разрешимых обращённых задач, а Р – потенциал обращения задачи.
Таким образом, измеряя данную характеристику можно говорить об эффективности использования данной задачи для обращения, поскольку можно выбрать такую задачу, в результате обращения которой возможно получить значительную часть неопределённых (противоречивых) обращённых задач которые мало пригодны в процессе обучения математике.
Проиллюстрируем сказанное на конкретном примере.
Задача 1. Из двух городов расстояние между которыми 1620 км вышли одновременно навстречу друг другу два поезда. Скорость одного поезда равна 40 км/ч, а скорость второго поезда на 10 км/ч больше скорости первого. Найдите скорость второго поезда и время их движения до встречи.
Решение:
1) 40 + 10 = 50 (км/ч) – скорость второго поезда;
2) 50 + 40 = 90 (км/ч) – скорость сближения поездов;
3) 1620:90 = 18 (ч) – время встречи поездов.
Ответ: 50 км/ч, 18 ч.
Для начала подсчитаем потенциал обращения данной задачи. Прежде всего отметим, что условие У состоит из трёх элементов, а заключение Т исходной задачи – из двух элементов. Тогда потенциал обращения этой задачи, определяемый по формуле P = (2n – 1)∙(2k – 1), будет равняться:
P = (23 – 1)∙(22 – 1) = 7∙3 = 21, то есть в результате обращения исходной задачи 1 возможно получить 21 обращённую задачу.
Составим числовые цепочки структурных элементов решённой исходной задачи и всевозможных обращённых задач.
По этим числовым цепочкам структурных элементов обращённых задач определим меру обращения для каждого (из 21) случая.
Получим:
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
.
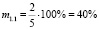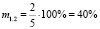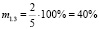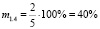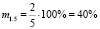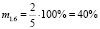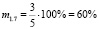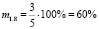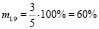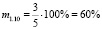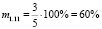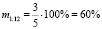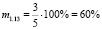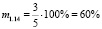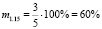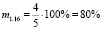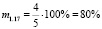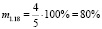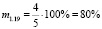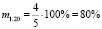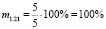Как можно увидеть, мера обращения исходной задачи 1 постепенно возрастает и достигает своего максимального значения в последнем случае, который соответствует получению обратной задачи. А теперь сформулируем условия обращённых задач по соответствующим им числовым цепочкам.
Задача 1.1. Из двух городов вышли одновременно навстречу друг другу два поезда и встретились через 18 ч. Скорость одного из них 40 км/ч, а другого – на 10 км/ч больше скорости первого. Найдите скорость второго поезда и расстояние между городами.
Решение:
1) 40 + 10 = 50 (км/ч) – скорость второго поезда;
2) 50 + 40 = 90 (км/ч) – скорость сближения поездов;
3) 90×18 = 1620 (км) – расстояние между городами.
Ответ: 50 км/ч, 1620 км.
Для того чтобы установить меру обратимости этой задачи, определим число переходов с прямого на обратное действие в решениях прямой и обращённой задач, используя при этом графовое представление процесса их решения. Графы их решений представлены на рис. 1.
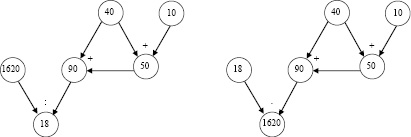
Рис. 1. Графы решений задач 1 и 1.1
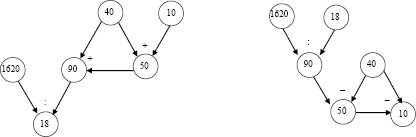
Рис. 2. Графы решений задач 1 и 1.3
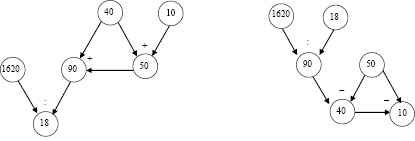
Рис. 3. Графы решений задач 1 и 1.17
Сопоставляя их, можно установить, что поскольку в решении обращённой задачи лишь одно действие (деление) изменилось на обратное (умножение), значит, число переходов мысли с прямого хода на обратный N′п/о = 1, а возможное количество переключений хода мысли с прямого на обратный Nп/о= 3, следовательно мера обратимости задачи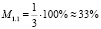 
.
Итак, выше мы установили, что приведённая задача имеет меру обращённости m1.1 = 40 %, а меру обратимости M1.1 ≈ 33 %.
Исследуем, все ли обращённые задачи, меры обращённости которых равны, имеют и равные меры обратимости. Для этого сформулируем условие обращённой задачи по числовой цепочке 1.3.
Задача 1.3. Из двух городов расстояние между которыми 1620 км вышли одновременно на встречу друг другу два поезда, которые встретились через 18 ч. Скорость первого поезда 40 км/ч. Найдите скорость второго поезда и укажите, на сколько скорость одного поезда меньше скорости другого.
Решение:
1) 1620:18 = 90 (км/ч) – скорость сближения поездов;
2) 90 – 40 = 50 (км/ч) – скорость второго поезда;
3) 50 – 40 = 10 (км/ч) – на столько скорость одного поезда больше другого.
Ответ: 50 км/ч, 10 км/ч.
Изобразим графы решений задач 1 и 1.3 (см. рис. 2).
Сопоставляя данные графы, можно увидеть, что в решении обращённой задачи 1.3 дважды происходит изменение прямого действия (сложение) на обратное ему (вычитание), значит, мера обратимости этой задачи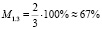 
.
Таким образом, мы получили, что, несмотря на то, что обращённые задачи 1.1 и 1.3, имеют равные меры обращённости m1.1 = m1.3 = 40 %, их меры обратимости различны, так M1.1 ≈ 33 %, а M1.3 ≈ 67 %. Имеет смысл проследить, а как поведёт себя мера обратимости задачи, т.е. уменьшится, или увеличится, либо останется неизменной, если её мера обращённости возрастёт. Например, сформулируем обращённую задачу 1.17, мера обращённости которой, как было указано выше, равна m1.17 = 80 %.
Задача 1.17. Из двух городов расстояние между которыми 1620 км вышли одновременно на встречу друг другу два поезда. Скорость одного из них равна 50 км/ч. Встреча поездов произошла через 18 ч. Найдите скорость другого поезда и укажите, на сколько скорость одного поезда больше скорости другого.
Решение:
1) 1620:18 = 90 (км/ч) – скорость сближения поездов;
2) 90 – 50 = 40 (км/ч) – скорость другого поезда;
3) 50 – 40 = 10 (км/ч) – на столько скорость одного поезда больше скорости другого.
Ответ: 40 км/ч, 10 км/ч.
Графы решений исходной задачи 1 и обращённой задачи 1.17 представлены на рис. 3.
Так, прослеживая действия решений на этих графах, заключаем, что мера обратимости задачи 1.17 составляет M1.17 =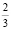 
∙100 % ≈ 67 %. В итоге, несмотря на то, что мера обращённости задачи 1.17 составляет m1.17 = 80 % и увеличилась по сравнению с мерой обращённости предыдущей задачи 1.3, у которой m1.3 = 40 %, мера же их обратимости осталась прежней и равной M1.3 = M1.17 ≈ 67 %. Более того, в ряде случаев обращений задач, приходилось констатировать тот факт, что несмотря на то, что обращённая задача не являлась обратной (m ≠ 100 %), тем не менее мера её обратимости оказывалась равна 100 %, т.е. имело место изменение всех прямых действий на обратные им.
Определим теперь меру продуктивности обращения задачи, которую вычислим по формуле:
,
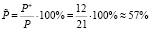где P+ = 12, поскольку разрешимыми являются лишь задачи 1.1 – 1.9, 1.16 – 1.18, а Р = 21.
Как видим, мера продуктивности задачи 1 является не высокой, поскольку практически половина обращённых задач являются неразрешимыми, но учитывая тот факт, что всего получена 21 обращённая задача, то можно считать, что данная задача вполне эффективна для обращения и её дидактический потенциал для развития гибкости мышления учащихся вполне ощутимый. Подчеркнём, что обращение задач является важным и перспективным направлением методической работы, позволяющим существенно усиливать развивающую значимость технологии обучения школьников математике [3].
Библиографическая ссылка
Абрамова О.М. ХАРАКТЕРИСТИКИ ОБРАЩЁННЫХ ЗАДАЧ В КОНТЕКСТЕ АНАЛИЗА ВОЗМОЖНОСТЕЙ ИХ ИСПОЛЬЗОВАНИЯ С ЦЕЛЬЮ РАЗВИТИЯ ГИБКОСТИ МЫШЛЕНИЯ СОВРЕМЕННЫХ ШКОЛЬНИКОВ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 10-5. – С. 896-901;URL: https://applied-research.ru/ru/article/view?id=7650 (дата обращения: 19.04.2024).