Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гришкан Ю.С. 1

---

1 Южный федеральный университет

Рассматриваются космологические решения уравнений движения для эффективных полевых мод в струнной сигма – модели Вселенной. Построены космологические решения для изотропной Вселенной на D – бране. Показано, что решение дефляционного типа в струнной метрике совпадает с решением Фридмана в метрике расширяющейся Вселенной.

Статья в формате PDF

1298 KB

теория струн

уравнения гравитационного поля

искривленное пространство – время

D – брана

расширяющаяся Вселенная

космологические решения Фридмана

1. Аshtekar А., Petkov V. (ed.). Springer Handbook of Spacetime. Springer-Verlag. Berlin – Heidelberg, 2014. – P. 1–839.

2. Гришкан Ю.С. Влияние нарушения лоренц-инвариантности на физические процессы в поздней Вселенной и жёсткое космическое гамма-излучение / А.А. Петрухин, М.Х. Хоконов // Сборник трудов 5-ой БМШ ЭТФ-2004. – М: МИФИ, 2005. – том 2. – С. 68–78.

3. Ellis J.R., Mavromatos N.E. and D.V. Nanopoulos, Physical Review Letters, – 1992. – v. B 293, p. 37–42/[arXiv:hep-th/9207103].

4. Antoniadis I., Bachas C., Ellis J.R., D.V. Nanopoulos. Liouville strings evidence. Physical Review Letters -1988- v. B 211 – p. 393- 397.

5. Гришкан Ю.С.// Сборник трудов 6-ой БМШ ЭТФ-2005 том 2 – 2005, – Москва, МИФИ – C. 72–86.

6. John Ellis, N.E. Mavromatos and D.V. Nanopoulos. The string coupling accelerates the expansion of universe./ [arXiv:gr-qc/0502119]. – 2005. – P. 1–6.

7. Хриплович И.Б. Общая теория относительности: учебн. для вузов-1 изд, – М: Институт компьютерных исследований, 2002. – С. 1–128.

8. Ландау Л.Д., Лифшиц Е.М. Теория поля: учебн. для вузов – 4 изд. – М: Наука,1988. – С. 1–503.

Как правило, космологические решения, описывающие эволюцию Вселенной, строятся для полей (гравитационного поля и поля темной энергии), которые описывают пространство-время расширяющейся Вселенной на разных стадиях эволюции. Однако, в последнее время возникла уверенность в том, что связанные с тем, что теория поля как классическая, так и квантовая не описывает некоторых существенных свойств наблюдаемого макроскопического мира и в частности, квантовые флуктуации.

Более фундаментальной структурой, чем полевая, является струнная структура пространства-времени [1], [2]. В этой теории струны занимают место полей и привлекаются для описания, как элементарных частиц, так и квантовых флуктуаций вакуума.

Уравнения движения для эффективных полевых мод в струнной сигма – модели согласно [3] имеют вид:

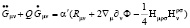(1)

где μ, ν,.. = 0,1,2,3, G_μν – метрика на струне, R_μν – эйнштейновская кривизна пространства-времени на бране, Ф – скалярное нелинейное дилатонное поле, H_μνρ – антисимметричный тензор, описывающий псевдоскалярное поле B, α’ постоянная – наклона Редже.

Совершенно нетривиальным является вопрос построения космологических решений в этой модели. Если в полевой модели время определяется одновременно с полем, то в эффективной модели струн Лиувилля в качестве времени выступает само дилатонное поле Ф – одно из фоновых полей модели. Поэтому необходимо отождествление этого псевдовремени Ф с мировым временем t. В ряде работ [4], [5] получена связь между t и Ф:

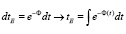. (2)

В результате, как показано в [4] эйнштейновское время в расширяющейся Вселенной связано со временем на мировой бране струнной сигма-модели соотношением

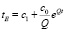, (3)

где c_1,0 – положительные константы.

При построении решений уравнений (1), динамическая эволюция этих решений прослеживается во времени t D – браны, для которой и справедливы уравнения (1). Любое точное космологическое решение может быть переведено из этого времени во время наблюдаемой нестационарной эйнштейновской вселенной с помощью формулы (3). Основной трудностью в построении струнной космологии является трудность, связанная с классификацией стадий динамической эволюции струнной структуры. Эта проблема связана с тем, что аппарат, привлекаемый для описания эволюции струнной структуры во времени содержит характерные черты двух разных подходов к описанию микро и макромира – теории рассеяния и динамической теории эволюции во времени [5].

Отражением этой дилеммы в математическом аппарате теории является отсутствие функциональной динамической связи между временем рассеяния частицы на D – бране, которое зафиксировано вструнной метрике G_ik(t) (и в котором описывается динамическая эволюция мира на бране) со временем расширяющейся Вселенной.

Наша идея состоит в построении космологических решений во времени t с последующим переводом их в космологическое время наблюдаемого мира t_E по формуле (3). Если при этом будут получены физически осмысленные известные космологические решения, то тем самым удастся построить последовательность во времени эволюции мира на бране, соответствующего эволюции коллективных мод струнной космологической модели с учетом флуктуаций геометрии мира.

Совершим внешне парадоксальный шаг. Построим космологические решения, описывающие стадию инфляции на бране. Для чего согласно [3] отожествим дилатонное поле со временем по формуле:

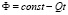, (4)

где Q – константа, называемая «центральный заряд браны»

Для удобства положим постоянную наклона Редже α’ = 1. Тогда согласно (1) и (4) уравнения примут вид:

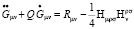. (5)

Решение для поля B будем искать, как и в работе [5] в виде:

B = βt, (6)

где β = const.

Зададим метрику на D-бране в стандартном 4-м космологическом виде

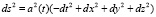, (7)

то есть,

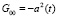
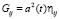(8)

где

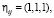
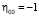. (9)

Тогда детерминант метрики можно представить в виде:

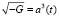. (10)

Таким образом, напряженность псевдоскалярного поля можно записать в виде

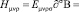
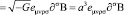(11)

где E_μνρσ – 4-мерный ковариантный антисимметричный символ Леви – Чивита.

Следуя (6) и (11), получаем:

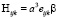(12)

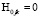. (13)

Теперерь уравнения (1), описывающие эволюцию мира во времени D-браны упрощаются:

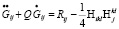(14)

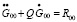(15)

В результате расчетов получим далее компоненты тензоров R₀₀, R_ij как функции масштабного фактора модели a(t) и вычислим его. Количество независимых констант модели может быть уменьшено, если предположить, что временное направление на бране не искривлено R₀₀ = 0 и центральный заряд на бране выражен так, чтобы решение имело инфляционный характер:

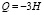. (16)

Тогда компоненты тензора кривизны Риччи примут вид [6, 7]:

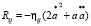, (17)

где точкой обозначена производная по времени

.

Преобразуем произведение напряженностей поля:

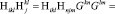
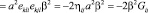(18)

Таким образом, можно записать на основании (17) и (18):

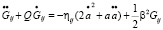(19)

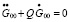(20)

Будем искать решение этих космологических уравнений в виде:

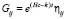(21)

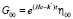(22)

где 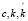– неизвестные константы.

Подставляя эти формулы в (19), (20), получим следующие соотношения между зависимыми константами модели:

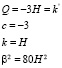(23)

Тогда космологические решения принимают вид:

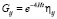(24)

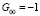. (25)

Построенное решение описывает быстрое экспоненциальное сжатие (дефляцию Вселенной на D-бране). Теперь необходимо перевести эти решения из времени на бране в эйнштейновское время расширения Вселенной. Для этого используем соотношение(3).

Расcчитаем выражение для масштабного фактора a(t_E) в наблюдаемой Вселенной.

Из (3), (24) следует

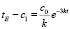(26)

Константа c₁ является тогда началом отсчёта времени t_E. Само эйнштейновское космологическое время

Введём обозначения, принятые в теории космологических моделей Фридмана. Обозначим момент начала расширения Вселенной как t₀ = c₁. Тогда

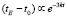(27)

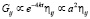(28)

Из (27), (28) следует

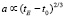(29)

Решение (29) есть космологическое решение Фридмана для физического времени t_E, описывающее расширение Вселенной на этапе динамического преобладания вещества над темной материей, т.е. стадия быстрого сжатия («дефляции» D-браны) соответствует, для наблюдателя, связанного с веществом, образующим расширяющийся мир, степенному расширению Вселенной по закону Фридмана в Общей Теории Относительности Эйнштейна [7], [8].

Построенное решения (29) позволяет связать заключительную стадию эволюции расширяющегося мира с одной из стадий динамической эволюции, входящих в его состав нелокальных дефектов, описывающих квантовые флуктуации метрики. А именно, дефляционное поведение нестационарной метрики D-браны соответствует расширению включающего внешнего мира по закону Фридмана для барионной материи.

Библиографическая ссылка