Считается, что магнитное поле создается только движущимися зарядами, так называемым молекулярным током и движущимися заряженными телами. Может ли незаряженное движущееся тело создавать магнитное поле, – вопрос, не лишенный смысла. Причиной появления магнитного поля могут быть в том числе и релятивистские преобразования скорости, принципиально отличающиеся от преобразований Галилея. Чтобы понять происхождение такого магнитного поля, достаточно рассмотреть две тождественные частицы, движущиеся со скоростями, равными по величине, но противоположными по направлению. В системе отсчета, связанной с центром масс частиц, суммарная скорость равна нулю. В лабораторной системе отсчета, относительно которой движется центр масс частиц, суммарная скорость нулю не равна. Именно это может стать причиной создания магнитного поля незаряженным движущимся телом [1]. К сожалению, такая простая интерпретация ожидаемого эффекта имеет ряд существенных недостатков. Во-первых, в реальных проводниках распределение зарядов, даже изотропное по направлениям движения в своей системе отсчета, в лабораторной системе отсчета не является изотропным. Это, в свою очередь, в той или иной степени может существенно подавить эффект. Кажутся нереальными оценки средней скорости классически движущихся в проводнике электронов. Лучше воспользоваться экспериментальными результатами, причем теми, которые могут быть интерпретированы с классической точки зрения. В противном случае, то есть при попытке объединить квантовую механику с классической, можно получить то, что является результатом превышения точности. И самое основное: простые оценки предсказывают аномально большое значение индукции магнитного поля, создаваемого телом, скорость которого относительно лабораторной системы далека от релятивисткой [1]. В экспериментах [2,3] такое, разумеется, не наблюдается. Причина понятна. Это – существенно завышенное значение классической плотности носителей тока в проводнике. С другой стороны, пока нет причин отвергать эффект. Разумных и адекватных оснований для этого пока нет. Поэтому актуальным становится экспериментальное обнаружение эффекта. Экспериментальное исследование явления может стать инструментом, позволяющим выяснить, как на самом деле распределены носители тока в проводнике. Судя по всему, задача должна быть решена в наиболее общем виде, стимулирующем в том числе и планирование эксперимента. Чрезвычайно слабое постоянное магнитное поле, скрытое за магнитными полями Земли, лабораторного оборудования и окружения, обнаружить крайне трудно, а иногда и практически невозможно.
Пусть в системе отсчета X/Y/Z/, движущейся относительно системы отсчета XYZ со скоростью vO, скорость электрона v/ имеет компоненты vx/,vу/,vz/. Тогда в лабораторной системе отсчета XOYOZO, повернутой на угол j вокруг оси Z другой лабораторной системы XYZ (рис. 1), скорость v/ будет иметь компоненты
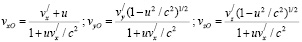 . (1)
. (1)
Переход к лабораторной системе отсчета, в точке P которой рассматривается магнитное поле, отвечает преобразованиям поворота:
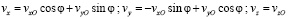 . (2)
. (2)
Поскольку скорость u каждой точки вращающейся с угловой скоростью w части тонкого диска мала по сравнению со скоростью света c, то преобразования (1), являющиеся следствиями специальной теории относительности, применимы, даже если одна из систем отсчета, конкретно X/Y/Z/, является вращающейся, то есть, не инерциальной.
Индукция магнитного поля, создаваемого движущимся со скоростью v зарядом dq в точке P лабораторной системы отсчета XYZ равна
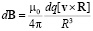 , (3)
, (3)
где
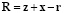 , (4)
, (4)
а неизменные векторы z и x определяют положение точки наблюдения P в лабораторной системе отсчета.
Нас будет интересовать Z-компонента индукции магнитного поля, поэтому
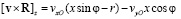 . (5)
. (5)
Пусть dV – элемент объема в системе отсчета XYZ, в системе отсчета X/Y/Z/ ему отвечает элемент объема
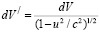 . (6)
. (6)
Так как элемент объема фазового пространства инвариантен по отношению к преобразованиям Лоренца, то инвариантной является и функция распределения [4], поэтому
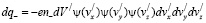 , (7)
, (7)
– отрицательный заряд, находящийся в точке, определяемой радиус-вектором r, и поскольку положительный заряд dq+ предполагается покоящимся в системе отсчета X/Y/Z/ (vxO=u) , то
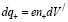 , (8)
, (8)
и для них
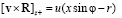 .
.
При малых скоростях u, vx/ и vy/
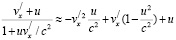 (9)
(9)
и
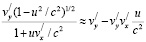 . (10)
. (10)
Поскольку вероятность обнаружить частицу с любыми значениями компонент скоростей vy/ и vz/ в пределах –∝<vy/<∝ и –∝<vz/<∝ равна единице
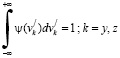 ,
,
а среднее значение компонент скоростей равно нулю
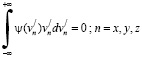 ,
,
то в нерелятивистском приближении от разложений (9) и (10) остаются только два слагаемые
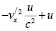 ,
,
дающие ненулевой вклад в индукцию магнитного поля, создаваемого электронами:
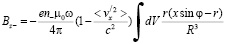 , (11)
, (11)
где dV=hrdrdj; u=ωr; h – толщина части диска и <vx/2>=<v/2>/3»<v2>/3 – среднее значение квадрата X-компоненты скорости в системе отсчета вращающегося тела.
Обязательно следует обратить внимание на индукцию магнитного поля, создаваемого положительными покоящимися в системе отсчета X/Y/Z/ зарядами:
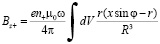 , (12)
, (12)
что при условии электрической нейтральности тела –en–+en+=0 означает
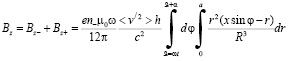 . (13)
. (13)
Удобно ввести автомодельные переменные r=r/a; c=x/a; z=z/a и полагая v/=v, записываем при h<<a
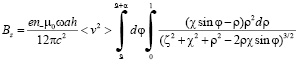 . (14)
. (14)
Прежде, чем анализировать этот результат, имеет смысл оценить коэффициент, имеющий размерность индукции магнитного поля, стоящий перед безразмерным интегралом. Сопоставляя работу выхода для Al со средней кинетической энергией электрона, получаем <v2>≈1.3⋅1012 м2/с2. Концентрацию носителей тока для того же алюминия удобно оценить, исходя из экспериментальных значений постоянной Холла [5] или термоэлектрических данных [6]: 1/n-e≈3×10-10м3/Кл [5,6]. Это дает n–=4.8⋅1029 м-3. Отсюда при a=2.5 см; h=0.8 см и n=w/2p=50 Гц, получаем
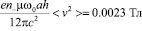 .
.
Это – более разумное значение по сравнению с тем, что предсказано ранее [1], но, правда, очень завышенное. Для сравнения: индукция магнитного поля Земли как минимум в тысячу раз меньше. Судя по всему, такое чрезвычайно завышенное значение возникло из-за очень большого значения электронной плотности. Не исключено, что слишком большим является и средний квадрат скорости электронов в металле. Проблема осталась: с одной сторона нейтральный вращающийся диск или его часть должны создавать магнитное поле, а с другой – вычисленное значение индукции магнитного поля оказалось слишком большим.
Такой сравнительно громоздкий расчет выполнен не зря. Кстати говоря, для диска (угол раствора сектора a=2p) на оси вращения, то есть при x=0, выражение (14) приобретает чрезвычайно простой вид:
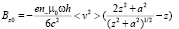 . (15)
. (15)
То, что следует исключить полностью, так это всякие подозрения, касающиеся справедливости преобразований скорости (1) или корректности постановки задачи. Классический подход к описанию кинематики носителей заряда в металлах удовлетворительно проявил себя в интерпретации закона Ома и закона Био-Савара. Была слабая надежда, что учет распределения по скоростям и по направлениям сведет индукцию магнитного поля либо к очень малой величине, либо к нулю. Этого не случилось. С другой стороны, простота и наглядность конечного результата, справедливость для любой функции распределения – от распределения Максвелла до вероятности обнаружить осциллятор с заданной скоростью – вот почему решение кажется настолько полным, чтобы на это не обращать внимание. Практически нет надежды на прямой расчет, избавленный от разложений (9) и (10). В этом случае индукция магнитного поля обязана зависеть не только от квадрата средней скорости, но и от особенностей функции распределения, а значит, тождественно нулю равна не будет.
Не исключено, однако, что в данной задаче классический подход парадоксальную роль. В любом случае все это полезно. Если есть вопросы, значит рано или поздно должны появиться и ответы. Так устроена природа: то, что должно произойти – рано или поздно случится, и это поле обязательно себя проявит. Пока же ответ приходится ждать только от эксперимента. Именно по этой причине пришлось решить по возможности общую задачу, то есть рассмотреть не вращающий диск, а его часть. Как и ожидалось, в этом случае магнитное поле является переменным (рис. 2). Более того, оно очень быстро спадает с увеличением расстояния z от плоской поверхности вращающегося диска. От угловой скорости вращения индукция магнитного поля зависит линейно. Это даст возможность отличить эффект от того, что может быть вызвано центробежным уходом электронов на периферию диска или его части.
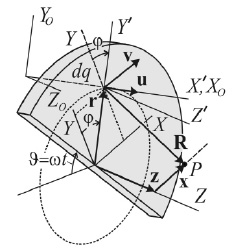
Рис. 1. Вращающееся нейтральное несимметричное тело
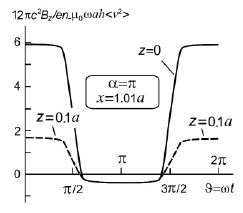
Рис. 2. Зависимость индукции магнитного поля от угла поворота при различных расстояниях z от плоской поверхности вращающегося тела
Библиографическая ссылка
Герасимов С.А., Дурыманов В.А. МАГНИТНОЕ ПОЛЕ ВРАЩАЮЩЕГОСЯ НЕЗАРЯЖЕННОГО ТЕЛА // Международный журнал прикладных и фундаментальных исследований. 2015. № 11-5. С. 614-618;URL: https://applied-research.ru/ru/article/view?id=7847 (дата обращения: 24.02.2026).

