Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Игошев П.А. 1 Игошев П.А. 2 Антипин Т.В. 1 Антипин Т.В. 2 Ирхин В.Ю. 1

---

1 Институт физики металлов УрО РАН

2 Уральский федеральный университет

В рамках обобщенного приближения Хартри-Фока для спирального магнитного порядка вычислена магнитная фазовая диаграмма основного состояния в периодической модели Андерсона на квадратной решетке. Последовательное рассмотрение фазовых переходов между различными магнитными фазами позволяет описать магнитное фазовое расслоение, возникающее как следствие скачка концентрации и амплитуды намагниченности при переходе первого рода. Показано, что физическая картина формирования спирального магнетизма для случаев целой и промежуточной валентности существенно различается. В случае целой валентности теория возмущений по обратному кулоновскому взаимодействию и глубине d-уровня приводит к эффективной s-d обменной модели. Последняя дает картину магнитного порядка, качественно близкую к ранее полученными результатами для модели Хаббарда.

Статья в формате PDF

1182 KB

спиральный магнитный порядок

зонный магнетизм

фазовое расслоение

периодическая модель Андерсона

1. Игошев П.А., Тимиргазин А.К., Аржников А.К., Ирхин В.Ю. Влияние электронных корреляций на формирование спиральных магнитных состояний в двумерной -модели Хаббарда // Письма в ЖЭТФ. – 2013. – Т. 98, №3. – С. 172-177.

2. Изюмов Ю.А., Курмаев Э.З. Материалы с сильными электронными корреляциями // УФН. – 2008. – Т. 178, №1. – С. 25-60.

3. Каган М.Ю., Кугель К.И. Неоднородные зарядовые состояния и фазовое расслоение в манганитах // УФН. – 2001. – Т. 171, №6. – С. 577-596.

4. Нагаев Э.Л. Разделение фаз в высокотемпературных сверхпроводниках и родственных им магнитных материалах // УФН. – 1995. – Т. 165, №5. – С. 529-554.

5. Arrigoni E., Strinati G.C. Doping-induced incom­mensurate antiferromagnetism in a Mott-Hubbard insulator // Phys. Rev. B. – 1991. Vol. 44. – P. 7455.

6. Igoshev P.A., Timirgazin M.A., Katanin A.A., Arzhnikov A.K., Irkhin V.Yu. Incommensurate magnetic order and phase separation in the two-dimensional Hubbard model with nearest- and next-nearest-neighbor hopping // Phys. Rev. B. – 2010. Vol. 81. – P. 094407.

7. Igoshev P.A., Timirgazin M.A., Arzhnikov A.K., Irkhin V.Yu. Spiral magnetism in the single-band Hubbard model: the Hartree-Fock and slave-boson approaches // J. Phys.: Cond. Matt. – 2015. Vol. 27. – P. 446002.

8. Schrieffer J.R., Wolff P.A. Relation between the Anderson and Kondo Hamiltonians // Phys. Rev. – 1966. Vol. 149. – P. 491.

9. Visscher P.B. Phase separation instability in the Hubbard model // Phys. Rev. B. – 1973. Vol. 10. – P. 943.

10. de Carvalho Costa N., Pimenel de Lima J., dos Santos R.R. Spiral magnetic phases on the Kondo Lattice Model: A Hartree-Fock approach // Cond-mat.str-el. 2.06.15. URL: http://www.arxiv.org/abs/1506.00890v1.

В последние годы классическая проблема связи магнитных свойств сильно коррелированных соединений переходных металлов с геометрией решетки и электронной структурой продолжает привлекать внимание исследователей. Чтобы получить физическую картину магнитного порядка, необходимо учитывать, наряду с влиянием электронных корреляций и спиральным (неколлинеарным) магнитным порядком, магнитное фазовое расслоение, возникающее при переходах первого рода (первое свидетельство о существовании этого явлении было получено в работе [9]), и влияние многоорбитальных эффектов. Кроме того, спиральный магнитный порядок может играть важную роль в механизме перехода металл-изолятор [1]. Для исследования формирования магнитного порядка используются различные многоэлектронные модели, такие как модель Хаббарда, s-d обменная модель и периодическая модель Андерсона. Эти модели широко применяются для описания свойств соединений переходных и редкоземельных металлов, высокотемпературных сверхпроводящих купратов, систем с тяжелыми фермионами [2,5]. Формирование магнитных спиралей было исследовано в рамках невырожденной модели Хаббарда [1,7], однако влияние гибридизации электронных состояний на конфигурацию магнитного порядка требует дополнительных исследований. Целью настоящей работы является изучение магнитной фазовой диаграммы периодической модели Андерсона для квадратной решетки с учетом магнитного фазового расслоения, а также неколлинеарных магнитных состояний и их взаимосвязи. Поставленная задача позволит пролить свет на роль многоорбитальных эффектов в формировании спирального магнитного порядка.

Формализм

Гамильтониан системы имеет вид

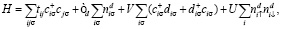(1)

где 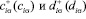– операторы рождения (уничтожения) s-электрона в зоне проводимости и локализованного d-электрона на узле i, обладающих проекцией спина 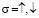, соответственно, 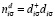– оператор числа локализованных электронов на узле i, обладающих проекцией спина 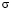, 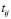– интеграл переноса между узлами i и j, 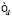– энергия локализованного электронного состояния, V – sd-гибридизация на одном узле, последний член отвечает за кулоновское взаимодействие d-электронов на одном узле. Полная концентрация электронов в системе

,

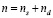где 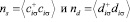– числа заполнения для зонного и локализованного состояний соответственно (⟨...⟩ – статистическое среднее).

Предположим, что имеет место спиральный магнитный порядок в плоскости xy, модулированный волновым вектором Q

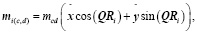(2)

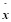где и 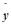– единичные векторы координатных осей, 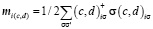– оператор намагниченности на узле, 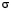– вектор матриц Паули. Выполняя локальный поворот в спиновом пространстве на узле i, что позволяет совместить направление намагниченности на разных узлах,

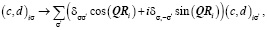(3)

и используя стандартное приближение Хартри-Фока для представления кулоновского взаимодействия в новой системе координат

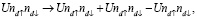(4)

мы получим гамильтониан спирально упорядоченной системы в обобщенном приближении Хартри-Фока.

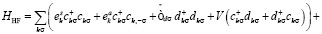
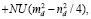(5)

где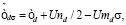

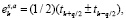
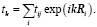
При решении уравнений обобщенного приближения Хартри-Фока выполнялась численная диагонализация гамильтониана (5) на сетке 100×100 в зоне Бриллюэна. Для определения энергетически выгодной спиральной фазы (в число которых включаются ферромагнетизм с Q=0 и антиферромагнетизм с 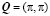) вычислялся и минимизировался термодинамический потенциал 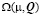для каждого волнового вектора Q спирали, выбранного на достаточно большой сетке в зоне Бриллюэна 20×20 [1,6], где µ – химпотенциал. Варьируя химпотенциал, можно определить зависимость магнитной конфигурации кристалла от концентрации носителей, в том числе и с учетом магнитных переходов первого рода, возникающих при условии 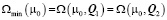. В этом случае при 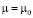параметры магнитного упорядочения испытывают скачок от 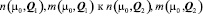и система при 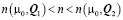неустойчива как однородная (явление «магнитного» фазового расслоения).

Если d-уровень лежит значительно ниже энергии Ферми и 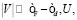гамильтониан (1) может быть сведен с помощью преобразования Шриффера-Вольфа [8] у s-d модели с параметром обмена

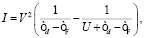(6)

где 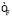– уровень Ферми.

Результаты. Результаты вычислений, описанных в предыдущем разделе, представлены на рис. 1–4. На фазовых диаграммах спиральные фазы идентифицированы видом их волнового вектора. Закрашенная область ‘’Ф1+Ф2» означает фазовое расслоение между фазами Ф1 и Ф2. Толстые линии означают переходы второго рода, тонкие линии – границы области фазового расслоения.

На рис. 1 представлен пример магнитной фазовой диаграммы основного состояния в переменных 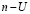для случая 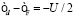, когда имеет место частично-дырочная симметрия.

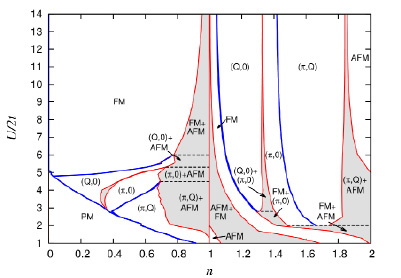
Рис. 1. Магнитная фазовая диаграмма основного состояния решеточной модели Андерсона в переменных n–U для случая 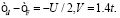«AFM» – антиферромагнитный порядок с 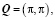«FM» – ферромагнетизм

При 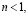когда перенос тока осуществляется d-состояниями и наша модель каноническим преобразованием сводится к эффективной модели Хаббарда, для достаточно больших U доминируют ферро- и антиферромагнитное упорядочение (между ними имеется фазовое расслоение), при меньших U – спиральный магнитный порядок. При 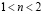для всего диапазона значений U, за исключением достаточно малых, доминирует спиральный магнитный порядок. Вблизи половинного заполнения 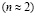имеется антиферромагнитная область.

На рис. 2 представлен пример фазовой диаграммы основного состояния в переменных 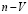для случая умеренных значений 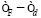и U, что обеспечивает нецелое заполнение локализованного состояния (см. рис. 4, случай промежуточной валентности). Видно, что распределение фаз на фазовой диаграмме для случаев 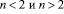существенно отличаются.

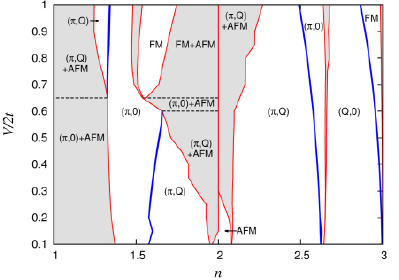
Рис. 2. Фазовая диаграмма основного состояния решеточной модели Андерсона с U=12t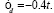 Слева: 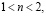справа: 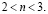Обозначения фаз те же, что и на рис. 1

При n=1 и n=2 имеет место шахматный антиферромагнитный порядок, при легировании в области 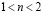возникает область магнитного фазового расслоения: при малых 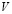– с участием «параллельной» спиральной фазы, при большем V и 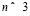– с участием ферромагнитной фазы, причем ее ширина в обоих случаях существенно превышает соответствующую область для невырожденной модели Хаббарда [1,6,7]. С другой стороны, при 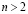и значительном легировании фазовое расслоение практически исчезает. Таким образом, картина магнитного упорядочения является существенно ассиметричной по отношению к знаку носителей заряда.

Совершенно иная картина наблюдается для случая целой валентности, что реализуется для 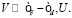Пример такой фазовой диаграммы представлен на рис. 3. Видно, что фазовая диаграмма практически симметрична по отношению к знаку носителей заряда, а распределение фаз подобно случаю промежуточной валентности при 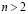. Физически реализуется случай решетки локализованных магнитных моментов, взаимодействующих друг с другом через электроны проводимости (подобно взаимодействию РККИ). Ясно, что в этом предельном случае реализуется спиральная фаза с волновым вектором, обеспечивающим максимальность функции Линдхарда

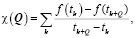(7)

где 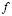– функция Ферми. Выражение для эффективного обмена дается формулой (6).

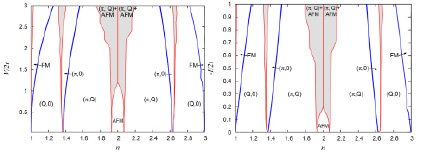
Рис. 3. Фазовая диаграмма основного состояния решеточной модели Андерсона с U=200t и 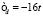. Слева: в терминах V, справа: в терминах эффективного s-d обменного параметра I

Наши результаты находятся в согласии с результатами s-d модели [10] при малом обменном параметре I (отметим однако, что спиральная фаза (Q,Q) полученная в это работе, оказывается нестабильной по отношению к фазовому расслоению между неелевской антиферромагнитной фазой и спиральной фазой 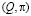). Кроме того, как можно видеть, последовательность магнитных фаз на рис. 3 качественно согласуются с результатами для невырожденной модели Хаббарда [6] при промежуточных U (концентрация носителей равна 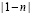для модели Хаббарда и 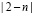для модели Андерсона). Однако, в отличие от модели Хаббарда, где при малых U реализуется парамагнитная фаза, в модели Андерсона (или s-d обменной модели) магнитные моменты не исчезают с уменьшением s-d обменного взаимодействия и парамагнитная фаза никогда не реализуется.

Чтобы проиллюстрировать поведение чисел заполнения для зонных и локализованных электронных состояний, на рис. 4 представлена их зависимость от концентрации электронов. Заметим, что направление намагниченности для s- и d-состояний противоположны. В случае 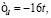соответствующем целой валентности 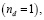фазовая диаграмма почти симметрична. С другой стороны, когда 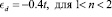мы имеем случай промежуточной валентности, а для 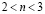– случай почти целой валентности. В этом случае фазовая диаграмма становится существенно ассиметричной. Для различных спиральных состояний степень насыщенности магнетизма (отношение намагниченности к числу носителей практически не зависит от концентрации как для s-, так и для d-состояний).

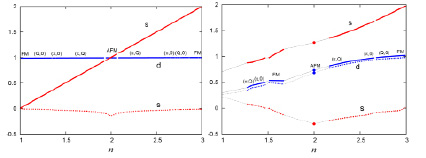
Рис. 4. Зависимость чисел заполнения (сплошная линия) и намагниченности на одном узле m (пунктирная линия) от концентрации электронов. Разрыв линий происходит при фазовом переходе первого рода, что связано со скачком волнового вектора Q спирального состояния. Тонкие линии соответствуют областям фазового расслоения. Обозначены типы спирального упорядочения. Слева: 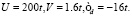Справа: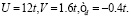

Заключение

Мы исследовали формирование спирального магнитного порядка для периодической модели Андерсона в различных режимах, включая случай целой и промежуточной валентности, и установили связь с другими многоэлектронными моделями. Мы показали, что картина формирования спиральных состояний и магнитного фазового расслоения, важного для кинетических явлений [3,4], существенно меняется по сравнению со случаем невырожденной модели Хаббарда. Однако и в том, и в другом случае реализуется богатое многообразие спиральных фаз. Эти результаты могут быть применены для объяснения электронных свойств соединений переходных металлов.

Работа поддержана проектом УрО РАН №15-8-2-9.

Библиографическая ссылка