Недавно международная группа исследователей презентовала в Nature [1] экспериментальное открытие циркулярной поляризации оптического послесвечений гамма – всплеска GRB 121024A. Объединив эти данные с наблюдением поляризации других гамма – всплесков (в частности, GRB 091018) эта группа получила, в достаточной мере, надёжную информацию о связи линейной и круговой поляризаций. В качестве источника поляризации излучения в оптическом диапазоне в подстрочнике письма предлагались ударные волны в хозяйской галактике. При этом, на современном уровне исследований не представляется возможным эти волны увидеть в том же оптическом диапазоне, что подтверждается приведёнными в работе цифрами. Основным результатом этого исследования является связь между циркулярной и линейной поляризациями V/L = 0.15.
Это открытие заставляет по-новому взглянуть на другие механизмы поляризации излучения, в частности, на механизм нарушения Лоренц- инвариантности (LV). Как будет показано ниже, LV механизм порождает именно такое излучение. В результате он остаётся конкурентоспособным в смысле объяснения возникновения поляризованных оптических волн рекордно – большой мощности. Именно высокая мощность излучения выделяет внегалактические гамма – всплески среди других явлений природы. Ошибочным является умозаключение о том, что LV нарушение неспособно генерировать поляризованные оптические волны, генерируемые в оптическом диапазоне. Как будет показано ниже, для оптического диапазона излучения отсутствует активная связь с гравитаций, в частности, осцилляции поляризационных параметров, но величина циркулярной поляризации от диапазона излучения не зависит.
Само явление LV связано с эффектом многомерности пространства. Пространство – время должно иметь минимум пять измерений, как это предполагалось в механизме Майерса – Поспелова. Поиск многомерности пространства является одним из приоритетных направлений развития современной физики. Именно к таким явлениям, с высокой степенью достоверности, относятся осцилляции нейтрино [2]. Другая возможность заключается в поиске явления LV в доступном современным установкам диапазоне энергий.
Дисперсионное соотношение для волн с нарушенной Лоренц – инвариантностью в общепринятой форме Майерса – Поспелова [3] (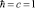 ) имеет вид:
) имеет вид:
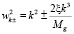 , (1)
, (1)
где 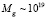 Гэв – планковская энергетическая шкала,
Гэв – планковская энергетическая шкала,
Здесь принято ограничение на параметр параметра нарушения лоренцц- инвариантности LV [4] ξ ≤ 3∙10–16.
Рассчитаем поляризационные параметры Стокса оптического излучения с нарушенной Лоренц – инвариантностью в гравитационном поле, следуя [5].
Выберем метрику стандартной модели расширяющейся Вселенной в виде:
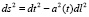 (2)
(2)
где 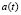 – масштабный фактор Вселенной.
– масштабный фактор Вселенной.
В статье [3] показано, что вектор –потенциал волны можно представить в виде:
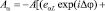
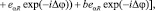 (3)
(3)
где 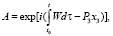
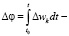 фаза смешивания поляризаций.
фаза смешивания поляризаций.
Рассчитаем напряжённость электрического поля волны в унитарной калибровке:
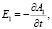
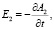 (4)
(4)
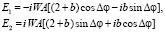 (5)
(5)
Пусть спектральная плотность принимаемого пакета плоских волн имеет вид n(P). Построим поляризационные параметры Стокса для этого пакета аналогично [3] с учётом нелинейных по параметру b смешивания поляризаций членов.
N = Ip = n(P)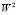 (
(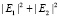 ) = = n(P)
) = = n(P)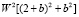 (6)
(6)
Q = n(P) 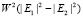 = = n(P)
= = n(P) 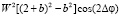 (7)
(7)
U = n(P) 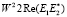 = – = n(P)
= – = n(P) 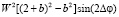 (8)
(8)
V = n(P) 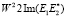 = = n(P)
= = n(P) 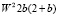 (9)
(9)
Построенные параметры образуют ортогональный поляризационный базис Стокса:
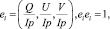 (10)
(10)
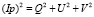 .
.
Рассчитаем линейную поляризацию рассматриваемого пакета плоских волн.
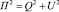 =
= 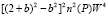 (11)
(11)
Квадрат мощности принимаемого волнового пакета
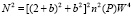 (12)
(12)
Выражение для линейной поляризации в рассматриваемой модели имеет вид:
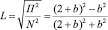 (13)
(13)
Эта кривая изображена на рис. 1.
Рассчитаем круговую поляризацию этого излучения
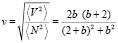 (14)
(14)
Эта кривая изображена на рис. 2.
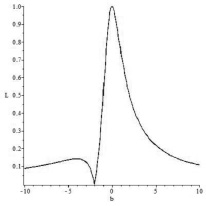
Рис. 1. Зависимость линейной поляризации L излучения гамма- всплеска от параметра смешивания b
Из (13), (14) видно, что линейная и круговая поляризации рассматриваемого оптического излучения зависят только от параметра смешивания поляризаций b и не зависит от от вида дисперсионного соотношения для волны.
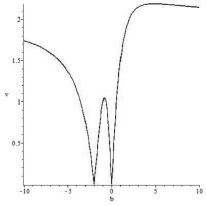
Рис. 2. Зависимость циркулярной поляризации v излучения гамма-всплеска от параметра смешивания b
Рассчитаем зависимость от времени t дисперсионного соотношения принимаемых волн.
Следуя [5], перепишем фазу смешивания поляризаций 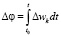 через квантовую поправку к частоте
через квантовую поправку к частоте 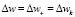 , релятивистскую частоту волны в метрике (2) как
, релятивистскую частоту волны в метрике (2) как 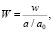
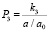 .
.
Из (1) следует, что поправка к дисперсионному соотношению для фотонов, вследствие нарушения Лоренц – инвариантности электромагнитного поля равна:
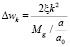 . (15)
. (15)
Как оказывается, от вида этой поправки зависят более тонкие поляризационные эффекты, связанные с различием скоростей левых и правых фотонов на нестационарном фоне расширяющейся Вселенной. Вследствие этого различия плоскость поляризации света поворачивается. На скорости этого поворота оставляет слепок расширение Вселенной.
Высчитаем приведённые поляризационные параметры
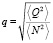 ,
, 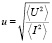 из (6)–(8).
из (6)–(8).
Эти параметры имеют вид:
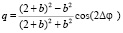 ,
,
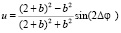 (16)
(16)
Согласно данным упомянутого выше эксперимента, циркулярная поляризация света меньше линейной v ≤ 0.15 но v/L < 1.
Строя графики поляризаций (13) (14) как функций получаем, что эти условия выполняются для интервала значений b = 0–0.14.
В литературе встречается и более жёсткий вариант ограничений на поляризацию оптического излучения: v = 0.15L.
Обобщим последнее условие с помощью нелинейного по параметру b уравнения
v = x L (17)
Легко показать, что это уравнение имеет единственный действительный корень x = b. Если x = 0.15, то едиственным действительным корнем уравнения (17) является b = 0.15.
То есть, амплитуда правой поляризации волны должна составлять менее 15 % от амплитуды левой поляризации. Эти наблюдения выявляют связь между и правой поляризациями света в источнике. Как видим, левая поляризация намного больше правой. Для установления механизма работы «центральной машины» гамма-всплеска это весьма существенно.
На рис. 3 построена зависимость v/L как функция параметра b.
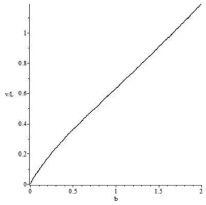
Рис. 3. Зависимость отношения поляризационного параметра v/L от красного смещения от параметра смешивания b
Параметры q, u (как и ) зависят от времени t. Значит q, u должны осциллировать по красному смещению. Эти параметры измеряются оптическими поляриметрами, что хорошо известно из наблюдения астрономических объектов. Обнаружение их осцилляций, поэтому, важно для обнаружения нарушения Лоренц – инвариантности электромагнитного поля 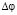 . В используемой системе единиц справедлива оценка по энергии [6], [7]
. В используемой системе единиц справедлива оценка по энергии [6], [7]
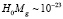 Гэв
Гэв
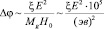 (18)
(18)
Нормируя (17) на энергию видимого света, 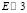 эв, получим оценку
эв, получим оценку
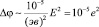 , (19)
, (19)
где 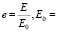 1 эв.
1 эв.
Для параметра ξ нарушения LV принято ограничение [4].
Наблюдение осцилляций [16] является тонким инструментом по измерению самого параметра ξ. Как видно из оценки (18) величина 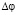 , согласно современным представлениям, мала. То есть, осцилляции по красному смещению, согласно современным представлениям отсутствуют. Обнаружение этих осцилляций и в оптическом и в рентгеновском диапазонах излучения одновременно дало бы основания для пересмотра современной теории LV.
, согласно современным представлениям, мала. То есть, осцилляции по красному смещению, согласно современным представлениям отсутствуют. Обнаружение этих осцилляций и в оптическом и в рентгеновском диапазонах излучения одновременно дало бы основания для пересмотра современной теории LV.
Согласно [3],
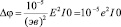 ,
,
где
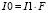
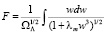 (20)
(20)
Предсказанные осцилляции поляризационных параметров q, u можно зарегистрировать при I1 = порядка 1.
Обозначим для удобства
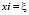 (21)
(21)
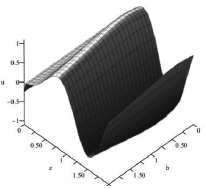
Рис. 4. Зависимость осцилляций поляризационного параметра q от красного смещения z и параметра смешивания b
На рис. 4 приведён трёхмерный график зависимости осцилляций параметра u от красного смещения z и параметра cмешивания
Библиографическая ссылка
Гришкан Ю.С. ПОЛЯРИЗАЦИЯ ИЗЛУЧЕНИЯ ПОСЛЕСВЕЧЕНИЙ ОПТИЧЕСКИХ ГАММА – ВСПЛЕСКОВ КАК СЛЕДСТВИЕ НАРУШЕНИЯ ЛОРЕНЦ – ИНВАРИАНТНОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ // Международный журнал прикладных и фундаментальных исследований. 2015. № 12-2. С. 236-239;URL: https://applied-research.ru/ru/article/view?id=7891 (дата обращения: 13.02.2026).

