В мире информационных технологий конечные поля Галуа GF(2m) имеют огромное практическое значение [1]. В частности, важнейшие алгоритмы обнаружения и исправления искажения информации в системах хранения и сетях передачи данных, использующие коды Рида-Соломона, а также криптографические алгоритмы (например, AES – Advanced Encryption Standard), защищающие информацию от несанкционированного доступа, базируются на арифметике конечных полей Галуа GF(2m).
Однако для эффективной программной и аппаратной реализации алгоритмов, также необходима быстродействующая аппаратная реализация арифметики поля Галуа GF(2m). В частности, для ускорения операций умножения и деления элементов поля применяют логарифмический подход, однако, здесь возникают дополнительные вопросы по реализации быстрого сложения и вычитания логарифмов.
В рамках научных исследований в области надежности систем хранения, передачи и обработки данных [3–9], а также методов информационного резервирования [2, 10], автором была исследована эффективная аппаратная схема сложения и вычитания логарифмов, и на базе нее была разработана схема арифметического процессора для поля Галуа GF(2m).
Арифметика поля Галуа GF(2m). Поле Галуа GF(2m), по определению являющееся полем многочленов вида 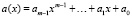 ,
, 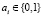 , образуется на базе простого поля Галуа GF(2) и нормированного примитивного неприводимого многочлена m-й степени:
, образуется на базе простого поля Галуа GF(2) и нормированного примитивного неприводимого многочлена m-й степени: 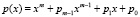 ,
, 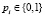 . Особо отметим, что элементы поля можно также рассматривать как m-разрядные двоичные числа
. Особо отметим, что элементы поля можно также рассматривать как m-разрядные двоичные числа 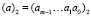 , и более того, для компактной формы представления записывать двоичные эквиваленты элементов поля в десятичной форме (а)10.
, и более того, для компактной формы представления записывать двоичные эквиваленты элементов поля в десятичной форме (а)10.
Например, поле Галуа GF(24) образуется при помощи неприводимого многочлена 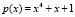 , и его элементы можно рассматривать как многочлены, так и соответствующие двоичные и десятичные эквиваленты:
, и его элементы можно рассматривать как многочлены, так и соответствующие двоичные и десятичные эквиваленты:
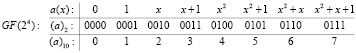
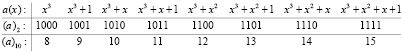
Отметим, что в базовом простом поле GF(2) для элемента 0 обратным элементом по сложению является сам элемент 0, также как и для элемента 1 обратным элементом по сложению является сам элемент 1. Соответственно, как сложение, так и вычитание элементов простого поля GF(2) фактически сводятся к одной и той же операции суммирования по модулю 2, и обозначается символом 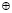 .
.
Тогда, при сложении и вычитании элементов поля GF(2m) мы имеем сложение соответствующих коэффициентов многочленов по модулю 2 (при представлении в виде многочленов) или побитовое сложение по модулю 2 соответствующих разрядов двоичных чисел (при представлении в виде двоичных чисел):
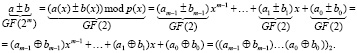 (1)
(1)
Пример 1. Найдем сумму элементов расширенного поля GF(24), представленных в виде соответствующих чисел «12» и «6» в десятичной системе счисления. Имеем,
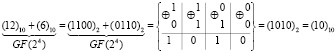 .
.
Что касается операций умножения (деления) элементов, то их можно свести к сложению (вычитанию) соответствующих дискретных логарифмов элементов поля по основанию примитивного элемента α поля Галуа GF(2m), и последующего вычисления степени примитивного элемента в степень суммы (разности) логарифмов.
 (2)
(2)
В качестве примитивного элемента обычно выступает элемент α(х) = х, который в десятичном представлении выглядит как (α)10 = 2, но в общем случае может быть и другой элемент поля (например, в криптографических алгоритмах (α)10 = 3). Особо отметим, что логарифмирование и возведение степень для максимальной скорости вычислений лучше производить табличным методом, причем таблицы подготавливать заранее для заданного поля GF(2m), с заданным неприводимым многочленом p(x) и примитивным элементом α, путем последовательного вычисления 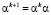 , причем
, причем 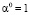 , k = 0…2m – 2.
, k = 0…2m – 2.
Так, например, для поля GF(24) таблицы степеней и логарифмов в двоичном и десятичном представлении элементов выглядят следующим образом:


Пример 2. Найдем произведение элементов поля GF(24), представленных в виде соответствующих чисел «5» и «7» в десятичной системе счисления. По «таблице логарифмов» для поля GF(24) имеем логарифмы элементов: 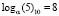 и
и 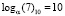 . Тогда получаем:
. Тогда получаем:
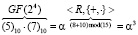 .
.
По «таблице степеней» для поля GF(24) имеем α3 = (8)10. Таким образом, результат равен (8)10.
Пример 3. Найдем отношение элементов «12» на «9» в поле GF(24). По «таблице логарифмов» для поля GF(24) имеем логарифмы элементов: 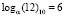 и
и 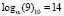 . Тогда получаем:
. Тогда получаем:
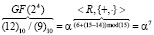 .
.
По «таблице степеней» для поля GF(24) имеем α7 = (11)10. Таким образом, результат равен (11)10.
Сложение и вычитание логарифмов элементов поля GF(2m). Теперь отметим то, что для аппаратной реализации операций умножения и деления элементов поля GF(2m) с использованием таблиц степеней и логарифмов, очевидно, что помимо ПЗУ, хранящих эти таблицы, потребуется функциональный узел сложения и вычитания логарифмов элементов поля. Учтем, что логарифмы с точки зрения алгебры вещественных чисел являются целыми неотрицательными числами в диапазоне 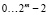 и их сложение / вычитание производится по модулю 2m – 1. Среди цифровых интегральных микросхем присутствуют, так называемые полные сумматоры, позволяющие складывать целые неотрицательные числа в диапазоне
и их сложение / вычитание производится по модулю 2m – 1. Среди цифровых интегральных микросхем присутствуют, так называемые полные сумматоры, позволяющие складывать целые неотрицательные числа в диапазоне 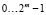 , представленные в виде m-разрядных двоичных чисел. Полные сумматоры также формируют выходной сигнал «переноса» в случае, когда сумма чисел больше 2m – 1 и не умещается в m разрядов. Также полные сумматоры имеют специальный вход для учета сигнала переноса от другого сумматора. То есть, фактически полный сумматор складывает три двоичных числа: два m-разрядных и одно 1-разрядное двоичное число, и формирует m + 1 – разрядную двоичную сумму. Особо отметим, что без разряда переноса, m-разрядная сумма, формируемая полным сумматором при сложении m-разрядных двоичных чисел u и v, это не что иное, как остаток (u + v) по модулю 2m, иными словами
, представленные в виде m-разрядных двоичных чисел. Полные сумматоры также формируют выходной сигнал «переноса» в случае, когда сумма чисел больше 2m – 1 и не умещается в m разрядов. Также полные сумматоры имеют специальный вход для учета сигнала переноса от другого сумматора. То есть, фактически полный сумматор складывает три двоичных числа: два m-разрядных и одно 1-разрядное двоичное число, и формирует m + 1 – разрядную двоичную сумму. Особо отметим, что без разряда переноса, m-разрядная сумма, формируемая полным сумматором при сложении m-разрядных двоичных чисел u и v, это не что иное, как остаток (u + v) по модулю 2m, иными словами 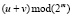 , а разряд переноса можно интерпретировать как целую часть от деления (u + v) на число 2m, иными словами
, а разряд переноса можно интерпретировать как целую часть от деления (u + v) на число 2m, иными словами 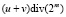 . Теперь заметим, что мы имеет место быть тождество
. Теперь заметим, что мы имеет место быть тождество
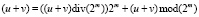 .
.
Преобразуем его следующим образом:
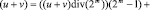
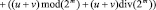 .
.
Теперь применим операцию вычисления остатка по модулю 2m – 1 к левой и правой части тождества, и тогда в итоге получим:
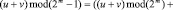
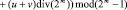 .
.
Тогда, очевидно, что для сложения m-разрядных двоичных чисел u и v по модулю 2m – 1 можно воспользоваться двумя полными сумматорами: первый будет осуществлять сложение чисел, вычисляя m-разрядную двоичную сумму 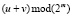 и перенос
и перенос 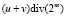 , а второй – складывать
, а второй – складывать 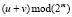 с переносом
с переносом 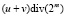 , как с одноразрядным двоичным числом, и на втором сумматоре будет получаться
, как с одноразрядным двоичным числом, и на втором сумматоре будет получаться
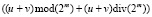 .
.
Однако, для получения итогового результата нужно еще вычислить остаток по модулю 2m – 1, но мы заметим, что в большинстве случаях 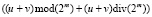 меньше 2m – 1, и вычисления остатка по модулю 2m – 1 излишне, кроме двух особых случаев, когда
меньше 2m – 1, и вычисления остатка по модулю 2m – 1 излишне, кроме двух особых случаев, когда 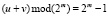 , а
, а 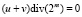 , и когда
, и когда
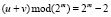 ,
,
а 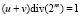 ,
,
в обоих случаях получается, что
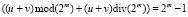 ,
,
и итоговым результатом должен быть 0. Заметим, что в m-разрядной двоичной сетке, число 2m – 1 несложно превратить в 0, прибавив к нему «лишнюю» 1 при возникновении особых случаев на втором сумматоре, используя его возможность складывать два m-разрядных и одно 1-разрядное число.
Наконец, для реализации операции вычитания логарифмов воспользуемся тождеством
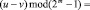
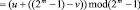 .
.
Также заметим, что 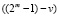 это не что иное, как «побитовая» инверсия разрядов m-разрядного двоичного числа v.
это не что иное, как «побитовая» инверсия разрядов m-разрядного двоичного числа v.
Тогда с учетом всего вышесказанного, можно использовать следующую схему сложения / вычитания логарифмов u и v по модулю 2m – 1, представленную на рис. 1.
Двоичное число u поступает непосредственно как первое слагаемое на первый сумматор. Двоичное число v поступает как второе слагаемое, предварительно пройдя элементы XOR, которые либо сохраняют его в неизменном виде в случае операции сложения (вход выбора операции Add/Sub = 0), либо осуществляют побитовую инверсию в случае операции вычитания (вход выбора операции Add/Sub = 1). Первый сумматор вычисляет m-разрядную сумму и одноразрядный перенос, которые поступают на второй сумматор, где m-разрядная сумма складывается с переносом, как с одноразрядным двоичным числом. Кроме того, если либо сумма равна 2m – 1, а перенос равен 0, либо сумма равна 2m – 2, а перенос равен 1, то при помощи многовходового элемента «И» и двухвходового элемента XOR формируется «лишняя» 1, которая также подается на второй сумматор, как слагаемое. В итоге на выходе второго сумматора получаем сумму или разность u и v по модулю 2m – 1.
Арифметический процессор для поля Галуа GF(2m) на базе схемы сложения и вычитания логарифмов. Теперь располагая узлом сложения / вычитания по модулю 2m – 1, и добавив к нему двухпортовое ПЗУ с таблицей логарифмов, а также ПЗУ с таблицей степеней, и некоторые вспомогательные узлы, можем рассмотреть арифметический процессор, выполняющий четыре основные операции с элементами поля Галуа GF(2m). Суммарная емкость двух ПЗУ составляет 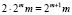 бит.
бит.
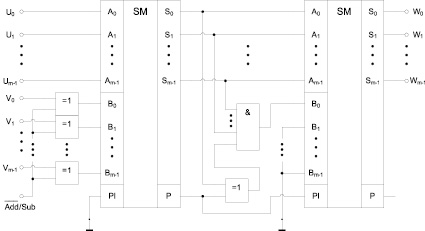
Рис. 1. Функциональная схема узла сложения и вычитания по модулю 2m – 1
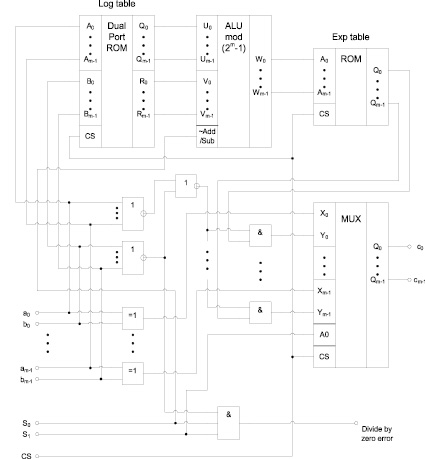
Рис. 2. Функциональная схема арифметического процессора для поля Галуа GF(2m) с использованием таблиц логарифмов по основанию и степеней примитивного элемента.
Ниже на рис. 2 представлена функциональная схема арифметического процессора. Ключевым элементом является m-разрядный выходной мультиплексор 2 → 1, который при управляющем сигнале S1 = 0 соединяет свои выходы с выходами элементов XOR, осуществляющих фактически сложение (оно же эквивалентно вычитанию) путем операции «побитового» XOR между входными операндами a и b – элементами поля GF(2m). При управляющем сигнале S1 = 1, мультиплексор подключает свои выходы к выходам ПЗУ с таблицей степеней, на вход которого, в свою очередь, поступает результат сложения (при управляющем сигнале S0 = 0) или вычитания (при S0 = 1) по модулю 2m – 1 логарифмов, извлекаемых из ПЗУ с таблицей логарифмов, одновременно по двум независимым шинам для обоих входных операндов a и b – элементов поля GF(2m).
Таким образом, при S1 = 0, и S0 = 0 или S0 = 1, выполняется операция сложения (вычитания) элементов поля путем одной и той же операции «побитового» XOR. При S1 = 1 и S0 = 0 выполняется операция умножения, а при S1 = 1 и S0 = 1 выполняется деление. Отметим также, что в схеме присутствует логическая схема, проверяющая равенство второго операнда b нулю, и при b = 0 в случае выбора операции деления, формируется специальный выходной сигнал ошибки деления на нуль – «divide by zero error». Управляющий вход CS (chip select) служит для активизации выходов микросхем ПЗУ и мультиплексора.
Заключение
Таким образом, в данной статье рассмотрены поля Галуа GF(2m), их арифметика, операции сложения, а также умножения и деления на базе логарифмов элементов поля. Также рассмотрена схема сложения и вычитания логарифмов элементов, а также предлагаемая автором схема арифметического процессора для поля Галуа.
Полученные результаты были использованы автором для разработки обучающей программы и лабораторных стендов для изучения студентами технических специальностей технологии кодирования информации при применении кодов Рида-Соломона.
Библиографическая ссылка
Рахман П.А. АРИФМЕТИКА ДВОИЧНОГО ПОЛЯ ГАЛУА НА БАЗЕ СХЕМЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ ЛОГАРИФМОВ И ЕЕ АППАРАТНАЯ РЕАЛИЗАЦИЯ // Международный журнал прикладных и фундаментальных исследований. 2015. № 12-3. С. 397-402;URL: https://applied-research.ru/ru/article/view?id=7941 (дата обращения: 25.12.2025).

