Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гришкан Ю.С. 1

---

1 Южный федеральный университет

Рассчитана степень анизотропии галактических космических лучей (эффект Комптона – Геттинга) с помощью релятивистских кинетических уравнений СТО и с помощью кинетических уравнений Общей Теории Относительности (ОТО). Второй вариант эквивалентен расчётам во вращающейся неинерциальной системе отсчёта.Показано, что оба результата совпадают друг с другом.

Статья в формате PDF

1554 KB

галактические космические лучи

анизотропия потока

кинетические уравнения

специальная теория относительности (СТО)

искривленное пространство – время

общая теория относительности (ОТО)

1. Алексеев Е.Н. и др. Анизотропия космических лучей с энергией ~ 2 Тэв по данным, полученным за 10 лет непрерывных наблюдений на Баксанском Подземном Сцинтилляционном телескопе ИЯИ РАН. // Известия РАН. Сер. Физическая. – 1995. – т. 59, в. 4. – С. 200–205.

2. Compton A.H., Getting I.A. An apparent effect of galactic rotation on the intensity of cosmic rays. // Physical Review. – 1935. – v. 47. – P. 817–822.

3. Хаякава C. Физика космических лучей, ч. 2. – М: Мир, 1974. – С. 1–342.

4. Захаров А.В. Макроскопическая гравитация: учебн. для вузов. – 1 изд. – М.: Янус – К, 2000. – С. 1–284.

5. Лифшиц Е.М., Питаевский Л.П. Физическая кинетика: учебн. для вузов. – 1 изд. – М: Наука, 1979. – С. 1–526.

6. Лифшиц Е.М. Теория поля: учебн. для вузов-4 изд. – М.: Наука, 1973. – С. 1–503.

7. Bailey Q.G., Kostelecky A.V. Non inertial reference frame in GTR // Physical Review. – 2006. – v. D 74. – P. 045001–045020.

Степень анизотропии не превышает нескольких процентов и зависит от направления. Наблюдаемую анизотропию обычно выражают, как вариацию потока j. Степень анизотропии характеризуется величиной

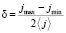(1)

где 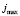, , 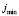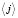– максимальная, минимальная и средняя интенсивности потока космических лучей.

В области энергий E < 10 ГэВ коэффициент анизотропии мал – δ < 10–3. При высоких энергиях эта ситуация меняется радикально и зависит от множества дополнительных факторов. Эксперимент показывает, что направление движения частиц концентрируется вблизи галактической плоскости. Частицы небольших энергий приходят из внутренней части Галактики, а больших энергий – из обеих частей. Существуют направления (кластер галактик Вирго), вдоль которых эти частицы концентрируются так, что коэффициент анизотропии растёт вплоть до значений δ < ~ 1. При регистрации анизотропии, являющейся важнейшей характеристикой потока космических лучей, используются все виды детекторов. Используемые детекторы базируются как на сцинтилляционных датчиках космического излучения, так и на черенковских. То есть, часто используются фотографии космической сферы в нейтринном свете и данные больших современных установок типа Суперкамиоканде.

Данные экспериментов по суточным вариациям космических лучей на Баксанском Подземном Сцинтилляционном Телескопе [1] приведены на рис. 1. Карта потока космических лучей по данным установки Суперкамиоканде приведена на рис. 2.

Эффект анизотропии, возникающий при движении Солнечной системы относительно галактических космических лучей называется эффектом Комптона – Геттинга (КГ) по имени его первооткрывателей [2], [3]. Пусть дифференциальный спектр первичных частиц представлен степенным законом, зависящим только от энергии E:

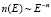, (2)

рα – импульс релятивистских частиц, rα – их координаты в собственной системе отсчета. Тогда для достаточно разреженных бесстолкновительных потоков в отсутствии внешних полей, кинетическое уравнение в (rp) пространстве будет иметь вид, аналогичный [4], [5]:

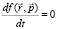(3)

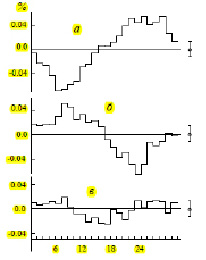
Рис. 1. Суточная анизотропия космических лучей по данным БПСТ

Дифференциальный поток j(E) и плотность частиц n(E) можно связать с функцией распределения следующим образом. Величина 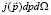есть число частиц в интервале 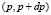внутри элемента телесного угла dΩ. Эти частицы за время dt пересекают поверхность dS, расположенную перпендикулярно 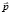. Элемент объема в 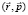пространстве равен 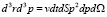. Полное количество зарегистрированных под всеми углами частиц является инвариантом и фигурирует в обеих частях нижеследующего равенства:

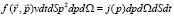(4)

где v ≈ c – скорость регистрируемых частиц.

С учетом связи между полной энергией и импульсом частиц (9) получаем связь между дифференциалами 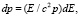а связь между потоком и фазовой скоростью принимает вид:

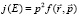. (5)

Дифференциальная плотность частиц для изотропного распределения примет вид:

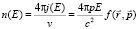(6)

Пример 1. Эффект Комптона – Геттинга в СТО [3].

Если рассматривать частицы в системе координат, которая движется со скоростью 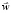, то импульс 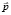частицы в системе покоя преобразуется в импульс 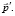Согласно СТО, преобразования Лоренца для импульсов имеют вид:

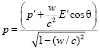. (7)

Так как скорость движения системы отсчета является нерелятивистской w<

Тогда, выражение для функции распределения в движущейся системе координат можно разложить в степенной ряд:

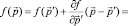
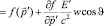(8)

Рассчитаем дополнительную часть потока частиц, связанную с движением системы координат, через поверхность, перпендикулярную 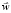, с помощью формул (75), (76):

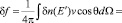
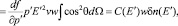(9)

где С(E) – коэффициент анизотропии Комптона – Геттинга. Из последних формул следует, что поток частиц под углом θ к w про- порционален 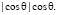Если интегральный поток частиц, пересекающих поверхность, перпендикулярную 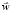, равен δf, то дифференциальная интенсивность, обусловленная потоком чатиц под углом θ, равна

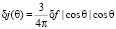(10)

Складывая (80) с интенсивностью фона изотропно распределенных частиц плотности n, которая равна vn/4π получаем

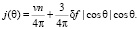
Поток δf связан с плотностью через КГ – коэффициент

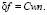(11)

Для степенного спектра частиц (2) отсюда следуют выражения для коэффициентов анизотропии потока

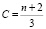(12)

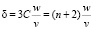(13)

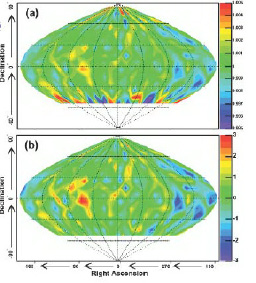
Рис. 2. Карта потока космических лучей в мюоном свете по данным установки Супер – Камиоканде. Интенсивность потока в условных единицах представлена на 1(a). На 1(b) представлено стандартное отклонение σ. Области анизотропии обозначены контрастом серого и черного тонов

Будем считать, что наблюдатель вращается либо вместе с Галактикой, либо в солнечной системе.

Рассчитаем анизотропию δ с помощью бесстолкновительной кинетической теории ОТО [4, 6]:

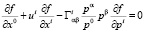(14)

Здесь и далее примем скорость света с = 1.

При 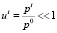(84) упрощается:

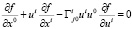(15)

При вращении Галактики и звездных систем сила Кориолиса значительно больше других неинерциальных сил [7]:

Поэтому, отличные от нуля компоненты метрики вращающейся системы отсчета примут вид:

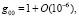
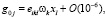
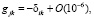(16)

где δik – тензор Кронекера, eikl – тензор Леви – Чивита, wk ~ 10–3/R0 – угловая скорость вращения, R0 – характерный масштаб исследуемой системы (например, галактики или солнечной системы).

Метрика (16) позволяет рассчитать символы Кристоффеля, играющие роль классических сил в кинетическом уравнении (15).

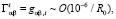
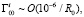
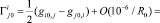
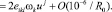(17)

По определению компонент 4 – импульса (9), в искомом приближении

.

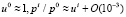Тогда кинетическое уравнение (85) примет вид:

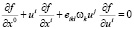(18)

Из (18) видно, что сила Кориолиса является в этом уравнении аналогом магнитной части силы Лоренца в уравнении электромагнитного поля.

Решение (18) для стационарного (не зависящего от времени) и однородного (не зависящего от координат) состояния f0 принимает вид:

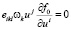(19)

Его решением является функция

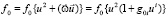, (20)

где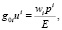

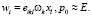
Разложим решение (90) в ряд по 1/E:

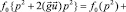
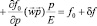(21)

здесь δf –анизотропная часть функции распределения, связанная с движением наблюдателя.

Соответствующие δf плотность δn и поток δj имеют вид:

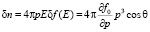(22)

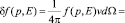
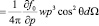(23)

Интегрирование (93) дает

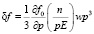. (24)

Подставляя в (24) степенной спектр (12), получим коэффициент КГ

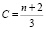, (25)

анизотропную часть потока

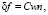(26)

полный поток

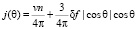(27)

и анизотропию космических лучей

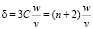. (28)

Из (13), (28) вытекает, что оба рассмотренных сериала по расчету анизотропии космического излучения за счет движения наблюдателя эквивалентны и приводят к одинаковым числовым значениям. Анизотропия за счет вращения Галактики 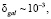анизотропия за счет собственного вращения Солнца .

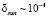Библиографическая ссылка