Известно, что обкатывание с силой превышающей определенное значение может привести к перенаклепу и как следствие шелушению обкатанной поверхности. Об этом свидетельствует и наличие экстремума у кривых зависимости шероховатости от погонной силы обкатки (рис. 1) [1].
При обработке жесткими обкатниками это явление может наступить при натяге ≈ 150…175 мкм [2]. Начало шелушения зависит от механических свойств обкатываевого материала, формы микронеровностей, условий смазки и режима обкатки. В.М. Браславским [1], для бочкообразных роликов, предложено определять это усилие по формуле:
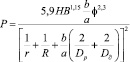(1)
где a и b – полуоси эллиптической площадки контакта; φ – средний угол вдавливания; Dp, r – диаметр и радиус профиля ролика; Dд, R – диаметр и радиус кривизны образующей детали.
Покажем как эта зависимость может быть применена для роликов конического профиля. Контурная линия контакта конического ролика с цилиндрической деталью имеет каплевидную форму (рис. 2), причем пятно контакта можно рассматривать как совокупность двух зон: зоны внедрения ролика – а1 в заготовку и зоны упругого восстановления (сбега) – а2. Геометрические параметры контакта могут быть определены по зависимостям приведенным в работе [3].
Приняв, что деформирующее усилие представляет собой равномерно распределенную по длине контакта нагрузку, полное усилие будет равно:
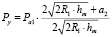(2)
где Ра1 – усилие действующее на участке внедрения; а2 – полуось контакта на участке упруго восстановления; hm – наибольшая глубина внедрения деформирующего ролика; R1 – радиус ролика на участке внедрения.
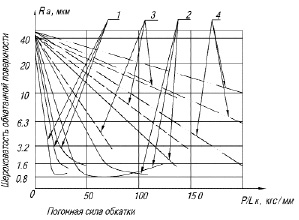
Рис. 1. Зависимость шероховатости от погонной силы обкатки роликами с прямолинейной образующей при диаметре ролика 3 мм (1), 5 мм (2), 12,5 мм (3), 32 мм (4) [1]
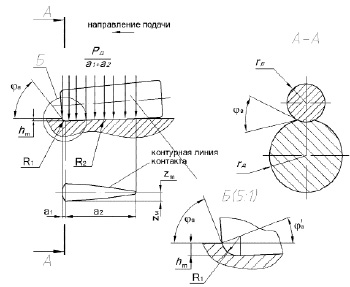
Рис. 2. Схема внедрения конического ролика в поверхность вала
Средний угол вдавливания определяется по формуле:
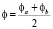(3)
где φa – угол вдавливания в направлении подачи; φв – угол вдавливания в направлении скорости обкатки.
Для определения угла φa рассмотрим схему внедрения ролика в направлении подачи (см. рис. 2, Б).
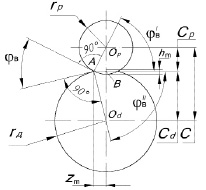
Рис. 3. Схема к определению угла вдавливания в направлении скорости обкатывания
; 
;
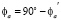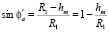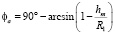(4)
Для нахождения угла φb рассмотрим схему внедрения ролика в сечении перпендикулярном продольной подаче (рис. 3).
Из этой схемы: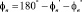 
Из прямоугольных треугольников ОрАВ и ОdАВ:
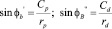
С другой стороны:
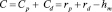
И, следовательно:
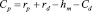
Катет AB = zm из тех же треугольников:
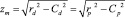
Откуда: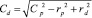 
Решая совместно полученные уравнения получим:
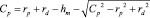
Откуда:
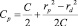(5)
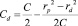(6)
Таким образом можно записать для синусов определяемых углов:
;
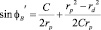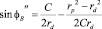
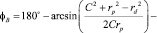
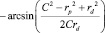(7)
Для нахождения отношения 
применим зависимости [3] для геометрических параметров контакта каплевидной формы:
;
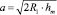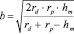(8)
Откуда:
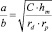(9)
Усилие, действующее на участке внедрения, будет определяться по формуле:
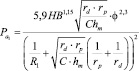(10)
Подставив полученную зависимость в формулу (2) получим зависимость силы деформирования от геометрических параметров контактной зоны, размеров контактирующих тел, а также механических свойств обрабатываемого материала, при которой возможно шелушение обрабатываемой ППД поверхности:
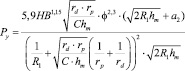(11)
Библиографическая ссылка
Никифоров Н.И. ОПРЕДЕЛЕНИЕ СИЛЫ ДЕФОРМИРОВАНИЯ ПРИ ППД СООТВЕТСТВУЮЩЕЙ НАЧАЛУ ШЕЛУШЕНИЯ В РЕЗУЛЬТАТЕ ПЕРЕНАКЛЕПА ПОВЕРХНОСТИ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 12-4. – С. 599-601;URL: https://applied-research.ru/ru/article/view?id=7984 (дата обращения: 21.11.2024).