В работах [1–3] показано, что атом водорода может находится в субатомных состояниях с энергией связи ε0 ~ 103 эВ. Субатомные состояния атома водорода возможны, если справедлива формула де Бройля.
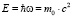
Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 представляет собой «сгусток» энергии, который должен двигаться по законам квантовой механики. Субатомные состояния атома водорода возможны тогда, когда расстояния между протоном и электроном настолько малы, что перекрываются области их пространственной локализации, вызванные наличием собственной квантовой энергии движения. В этих работах не была исследована устойчивость таких состояний при смещении протона относительно центра вероятности собственной локализации электрона. Рассмотрим подробнее этот принципиальный вопрос, от которого зависит величина энергии связи.
Постановка задачи
Уравнение Шредингера для субатома водорода записывается в виде:
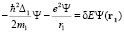 (1)
(1)
где δE = E1 ε0 > 0 и E1 = m1c2 – эйнштейновское выражение для энергии покоя электрона. Уравнение (1) было решено методом теории возмущений в сферической системе координат и была найдена волновая функция невозмущенного состояния электрона:
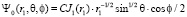 (2)
(2)
Здесь J1(r1) – функция Бесселя первого порядка. Далее необходимо вычислять энергию связи в виде:
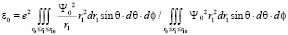 (3)
(3)
В интеграле (3) r0 – радиус области, которая недоступна для свободного электрона. Она определяется из условия, что угловая составляющая энергии движения не должна превышать его полную энергию. В области локализации свободного электрона нет барьеров и не может быть туннельных областей с отрицательной энергией. r10 – есть величина, определяемая первым нулем функции Бесселя J1(r10) = 0. Плотность вероятности нахождения электрона в области r1 ≤ r10 является наибольшей. Отношение амплитуд плотностей вероятностей в первой полуволне к амплитуде во второй составляет ~ 2,8. «Обрезание» интегралов связано с тем, что сама по себе плотность вероятности свободного электрона представляет собой неоднородную стоячую волну.
Вычисление энергии связи
Пусть протон смещается на радиус 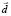 относительно вероятностного центра локализации электрона. Тогда уравнение (1) перепишется в виде:
относительно вероятностного центра локализации электрона. Тогда уравнение (1) перепишется в виде:
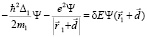 , (4)
, (4)
или в сферической системе координат
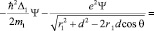
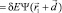 (5)
(5)
Вектор смещения 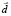 направлен вдоль оси z. Будем решать это уравнение методом возмущений, считая, что кулоновская энергия взаимодействия частиц мала по сравнению с эйнштейновской энергией покоя электрона. Тогда при вычислении энергии связи такой системы согласно формуле (3) возникают интегралы
направлен вдоль оси z. Будем решать это уравнение методом возмущений, считая, что кулоновская энергия взаимодействия частиц мала по сравнению с эйнштейновской энергией покоя электрона. Тогда при вычислении энергии связи такой системы согласно формуле (3) возникают интегралы
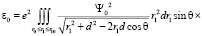
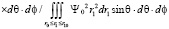 , (6)
, (6)
в одном из них можно выделить частный интеграл, определяющий зависимость энергии связи от смещения протона
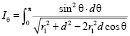 (7)
(7)
Чтобы не иметь дело с эллиптическими интегралами, вычислим это интеграл приближенно. Пусть d > r10 ≥ r1. В этом случае протон покидает собственную оболочку электрона. Воспользовавшись выписанным неравенством, имеем:
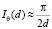 (8)
(8)
Энергия притяжения двух разноименных зарядов убывает по кулоновскому закону.
В другом предельном случае d < r1 ≥ r0, когда протон смещается в области недоступной для движения электрона, имеем:
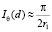 (9)
(9)
Протон может смещаться в пределах радиуса d < r0, при этом энергия связи субатома не изменяется.
Рассмотрим случай, когда r1 = d в области пространственного заряда электрона
Тогда вычисляя интеграл (7), получим
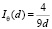 (10)
(10)
Сравнивая это выражение с формулой (8) можно видеть, что энергия связи в области пространственного заряда электрона убывает по кулоновскому закону с несколько меньшим коэффициентом. Имеет место «торможение» протона в области пространственного заряда электрона. Кулоновские силы притяжения (в системе координат вероятностного центра электрона) должны возвращать протон в область d < r0, где на протон не действуют силы. Иначе говоря, имеется пространственная область устойчивых субатомных состояний водорода.
Переформатируем уравнение (1) к виду:
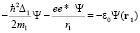 (11)
(11)
Уравнение (11) описывает «кулоновский» атом с эффективным зарядом e*, величина которого возрастает от центра системы по закону:
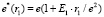 (12)
(12)
Для уравнения (11) с эффективным зарядом (12) пока не найдено аналитическое решение. Для оценки энергии связи субатома воспользуемся выражением для энергии связи атома водорода в виде:
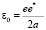 ,
, 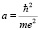 , (13)
, (13)
a – боровский радиус. Энергия связи в этой формуле зависит от величины эффективного заряда электрона, которая в свою очередь зависит от радиуса его локализации. Для свободного электрона его собственная область локализации пространственного заряда определяется спином. В составе субатома его спин не должен изменяться, стало быть, и границы области локализации остаются практически неизменными. Положим для оценок
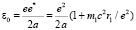 (14)
(14)
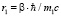
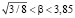
Коэффициент β учитывает область локализации пространственного заряда свободного электрона. Тогда из (14) получаем:
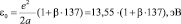 (15)
(15)
Для оценки энергии связи субатома получаем диапазон возможных значений:
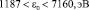
что согласуется вычислениями по теории возмущений ε ≈ 3∙103, эВ. Таким образом, найдена еще одна оценка энергии связи субатома.
Проблема образования субатомов водорода
Рассмотрим в общих чертах проблему образования субатомов водорода. В системе координат, связанной с протоном, электрон должен подлетать с энергией ~ ε0. Далее должно произойти резкое торможение электрона в области локализации протона и запас кинетической энергии должен быть передан окружающей электронной системе в виде многоэлектронных молекул с водородом, например, LiH, или твердому телу (аноду), на поверхности которого находится водород, например, в составе молекул воды. При этом должно наблюдаться тормозное излучение. По-видимому, такие условия эксперимента были созданы в работе [4].
В этой работе описаны результаты экспериментов по исследованию электрических взрывов фольг из особо чистых материалов в воде. Было обнаружено появление новых химических элементов и зарегистрировано «странное» излучение, которое не удалось идентифицировать (т.е., отнести к какому-либо из известных видов проникающей радиации). Напряжение на батарее конденсаторов, за счет разряда, который производились электровзрывы, составляло ≈ 4,8 кВ. Электроны с такой энергией вполне могут стимулировать образование субатомного водорода в воде. Компактность и высокая энергия связи субатомов водорода позволяет, на наш взгляд, приближаться им к ядрам других элементов на значительно более близкие расстояния и вступать с ними в ядерные реакции.
Заключение
В целом с помощью метода теории возмущений показано, что энергия связи субатома водорода является максимальной по абсолютной величине и устойчивой к возможным осцилляциям протона в области субатома и убывает по кулоновскому закону при разлете частиц.
Библиографическая ссылка
Неволин В.К. УСТОЙЧИВОСТЬ СУБАТОМНЫХ СОСТОЯНИЙ ВОДОРОДА // Международный журнал прикладных и фундаментальных исследований. 2015. № 12-4. С. 611-613;URL: https://applied-research.ru/ru/article/view?id=7987 (дата обращения: 10.03.2026).

