В [4] мы предложили новый подход к развитию математического аппарата электродинамики в направлении более адекватного описания перехода от одной инерциальной системы отсчета к другой на основе гиперконтинуальных представлений о пространстве и времени за счет совершенствования дифференциального исчисления полевых функций в предположении их зависимости от скорости движения наблюдателя. В плане такого совершенствования дифференциального исчисления полевых функций введены в рассмотрение глобально и локально транскоординатные дифференциальные уравнения электродинамики, использующие новые галилееву и транскоординатную производные полевых функций, а также новый дифференциальный оператор Дубровина, обобщающий оператор Даламбера.
В теории относительности электромагнитное поле тоже зависит от скорости движения наблюдателя, но только опосредованно через зависимость от нее интервалов времени и пространственных расстояний (преобразования Лоренца), следствием чего оказывается релятивистская инвариантность электрического заряда. Более фундаментальная же (непосредственная) зависимость поля от скорости сопряжена с наличием такой зависимости даже абсолютной величины электрического заряда. До последнего времени такая не инвариантность заряда подтверждалась лишь косвенными эмпирическими данными, заключавшимися в появлении электрического потенциала на сверхпроводящих обмотках и торах при введении в них постоянного тока, а также в наблюдении электрического импульса ядерных взрывов [10].
В частности, 9 июля 1962 года при взрыве в космосе над Тихим океаном водородной бомбы с тротиловым эквивалентом 1,4 Мт по программе США «Starfish» напряженность электрических полей превзошла предсказанные нобелевским лауреатом Бете Х.А. в 1000 раз. При взрыве термоядерного заряда в космосе по программе «Программа К», который был осуществлён в СССР осенью 1962 г, радиосвязь и радарные установки были блокированы на расстоянии до 1000 км примерно аналогично случаю вышеуказанного американского взрыва. Было обнаружено, что регистрация последствий космического ядерного взрыва возможна на больших (до 10 тысяч километров) расстояниях от места взрыва. Электрические поля импульса привели к большим наводкам на силовой кабель в свинцовой оболочке, закопанный на глубину ~ 1 м, соединяющий электростанцию в Акмоле с Алма-Атой. Наводки были настолько велики, что автоматика отключила кабель от электростанции.
Однако в 2015 году было получено уже прямое экспериментальное подтверждение этого феномена в результате обнаружения и исследования импульса электрического поля, возникающего при разогреве плазмы в результате разряда через разрядники конденсаторов большой ёмкости [10]. Оказалось, что в процессе разогрева плазмы при равном количестве в ней электронов и положительных ионов в ней образуется унитарный отрицательный заряд свободных электронов, не скомпенсированный более медленными положительными ионами.
Этот факт противоречит не только классическим, но и релятивистским преобразованиям электромагнитного поля при переходе от одной инерциальной системы отсчета к другой, свидетельствуя о несовершенстве не только классических, но и релятивистских представлений о пространстве и времени. Идея о том, что перспективная электродинамика должна предполагать существование зависимости электромагнитного поля от скорости движения наблюдателя, обусловленной не геометрией пространства-времени, а физической природой поля, не предполагающей инвариантность электрического заряда, развивалась в ряде работ Менде Ф.Ф., начиная с [8]. В этих работах, в частности, в [8, 10] приведено обоснование введения в электродинамику вместо классических и релятивистских новых преобразований электромагнитного поля, получивших название преобразований Менде.
Однако последовательное развитие такой радикальной идеи, как не инвариантность заряда, требует глубокого пересмотра математического аппарата электродинамики, призванного к созданию математических средств более адекватного описания перехода от одной инерциальной системы отсчета к другой. Подход к именно такому развитию математического аппарата электродинамики был как раз предложен нами в [4]. Этот подход лежит в рамках очередного пересмотра представлений о пространстве и времени с отказом от релятивистских и переходом к новым представлениям, которые мы называем гиперконтинуальными.
Понятие пространственно-временного гиперконтинуума введено в [1] в результате совместного изучения алгебраической и геометрической структур коммутативных алгебр с единицей, элементами которых являются функции синусоидальных волн. Гипотеза гиперконтинуума (об иерархической гиперконтинуальной структуре мирового физического пространства-времени) является отправной точкой научных исследований, направленных на обобщение представлений о структуре пространства и времени в русле перехода от современной квантовой научной парадигмы к новой системной, одновременно конструктивно соединяющей в своих рамках непрерывность и дискретность, динамичность и статичность, а также глобальность и локальность [3, 5, 6]. Иерархичность гиперконтинуума ограничивает применимость общепринятого принципа геометризации в физике и связанных с ним идей симметрии в геометрии за счет введения в теоретическую физику идей иерархичности [7, 9], эффективность которых апробирована нами при создании эталонной модели защищенной автоматизированной системы (ЭМЗАС) и математического аппарата ЭМЗАС-сетей [2].
Предложенный нами в [4] подход к развитию математического аппарата электродинамики, базирующийся на гиперконтинуальных представлениях о пространстве и времени, концепции не инвариантности электрического заряда и использовании новых галилеевой и транскоординатной производных полевых функций, приводит к переформулированию электродинамики с переходом от традиционной формулировки Герца-Хевисайда к новой формулировке, которую мы называем транскоординатной. При этом сразу возникает вопрос о том, какой вид имеют преобразования электромагнитного поля при переходе от одной инерциальной системы отсчета к другой, и будут ли эти преобразования преобразованиями Менде.
Цель исследования
Цель исследования – в рамках транскоординатной формулировки электродинамики и гиперконтинуальных представлений о пространстве и времени вывести преобразования электромагнитного поля при переходе от одной инерциальной системы отсчета к другой.
Материалы и методы исследования
Рассмотрим две инерциальные системы отсчета с единым для них временем ![]() ℝ. Одну из них (с системой прямоугольных декартовых пространственных координат
ℝ. Одну из них (с системой прямоугольных декартовых пространственных координат ![]() ) назовем лабораторной (не штрихованной) и будем интерпретировать ее, как относительно неподвижную. Вторую (с системой прямоугольных декартовых пространственных координат
) назовем лабораторной (не штрихованной) и будем интерпретировать ее, как относительно неподвижную. Вторую (с системой прямоугольных декартовых пространственных координат ![]() ) назовем субстанциональной (штрихованной) и будем интерпретировать ее, как связанную с некой движущейся реальной или воображаемой средой. Примем, что при t = 0 системы пространственных координат систем отсчета совпадают. Введем индексы
) назовем субстанциональной (штрихованной) и будем интерпретировать ее, как связанную с некой движущейся реальной или воображаемой средой. Примем, что при t = 0 системы пространственных координат систем отсчета совпадают. Введем индексы ![]() ,
, ![]() . Координаты по осям OX, OY, OZ и
. Координаты по осям OX, OY, OZ и ![]() ,
, ![]() ,
, ![]() будем задавать переменными xα и
будем задавать переменными xα и ![]() соответственно. Орты по осям OX и
соответственно. Орты по осям OX и ![]() , осям OY и
, осям OY и ![]() , осям OZ и
, осям OZ и ![]() обозначим через
обозначим через ![]() , причем
, причем ![]() , где δαβ – символ Кронекера. Через v и v обозначим вектор скорости движения субстанциональной системы отсчета относительно лабораторной и модуль этого вектора. Направляя орт e1 вдоль v, имеем:
, где δαβ – символ Кронекера. Через v и v обозначим вектор скорости движения субстанциональной системы отсчета относительно лабораторной и модуль этого вектора. Направляя орт e1 вдоль v, имеем: ![]() ,
, ![]() . Событие в данных двух системах отсчета имеет вид
. Событие в данных двух системах отсчета имеет вид ![]() ;
; ![]() , где
, где ![]() ,
, ![]() – радиус-векторы. Будем считать, что физическая эквивалентность событий
– радиус-векторы. Будем считать, что физическая эквивалентность событий ![]() и
и ![]() означает справедливость преобразования Галилея
означает справедливость преобразования Галилея
![]() (1)
(1)
или, иначе, заменяя векторное представление на компонентное,
![]() . (2)
. (2)
Электромагнитное поле в изотропной однородной среде без дисперсии описывается в лабораторной и субстанциональной системах отсчета своими переменными (напряженность электрического поля ![]() ,
, ![]() и магнитная индукция
и магнитная индукция ![]() ,
, ![]() ), постоянными (электрическая ε0 и магнитная μ0, а также выражающаяся через них скорость света в вакууме
), постоянными (электрическая ε0 и магнитная μ0, а также выражающаяся через них скорость света в вакууме ![]() ), параметрами (диэлектрическая и магнитная проницаемость ε и μ, а также плотность стороннего электрического заряда ρ, плотность электрического тока проводимости
), параметрами (диэлектрическая и магнитная проницаемость ε и μ, а также плотность стороннего электрического заряда ρ, плотность электрического тока проводимости ![]() , электрический заряд Q, электрический ток I), полевыми функциями
, электрический заряд Q, электрический ток I), полевыми функциями
![]() ,
, ![]()
, ![]() ,
,
![]() ,
,
причем
![]() ;
; ![]() . (3)
. (3)
В классической нерелятивистской электродинамике полагается:
![]() ;
;
![]() , (4)
, (4)
что математически выражает физическую концепцию инвариантности поля относительно скорости движения наблюдателя. Предлагаемые нами гиперконтинуальные представления о пространстве и времени [1] выходят за рамки этой концепции, но объясняют природу этой не инвариантности не геометрией единого пространства-времени подобно теории относительности, а фундаментальными свойствами поля. Данный взгляд на пространство, время и электромагнитное поле привел нас к новой формулировке электродинамики [4], которую мы называем транскоординатной, обобщающей общепринятую формулировку Герца-Хевисайда.
Интегральная форма уравнений Максвелла в представлении Герца-Хевисайда являет собой следующую систему четырех интегральных уравнений электродинамики:
![]() ;
; ![]() ;
;
![]() ;
;
![]() , (5)
, (5)
где s, l – произвольная двумерная замкнутая (для первых двух уравнений) или открытая (для вторых двух уравнений) поверхность и ограничивающий ее замкнутый контур, не обязательно совпадающий с электрическим контуром.
Область применимости (5) ограничена требованием состояния покоя контура l в лабораторной системе отсчета. Если снять это ограничение, потребовав лишь состояния покоя контура l в субстанциональной системе отсчета, то получится известное представление уравнений Максвелла (мы называем его транскоординатным [4]), интегральная форма которых будет являть собой в нем систему обобщающих (5) четырех интегральных уравнений электродинамики движущихся сред:
![]() ;
; ![]() ;
;
![]() ;
;
![]() . (6)
. (6)
Если транскоординатное представление уравнений Максвелла (как в рассмотренной интегральной, так и в рассматриваемой ниже дифференциальной формах) интерпретировать в контексте описания электромагнитного поля в пространственно-временном гиперконтинууме, то необходимо считать, что равенства (3) всегда выполняются, а (4) – в общем случае нет.
Дифференциальная форма уравнений Максвелла в представлении Герца-Хевисайда являет собой следующую систему четырех соответствующих интегральным уравнениям (6) дифференциальных уравнений электродинамики, относящихся к лабораторной системе отсчета:
![]() ;
; ![]() ;
; ![]() ;
;
![]() . (7)
. (7)
Уравнения (7) традиционно успешно используются в электродинамике, но при этом имеют существенный недостаток – область их применимости ограничена случаем совпадения лабораторной и субстанциональной систем отсчета (v = 0), то есть эти уравнения лишены математических средств адекватного описания перехода от одной инерциальной системы отсчета к другой, всецело привязывая процесс к одной (лабораторной системе отсчета).
В соответствии с предложенным в [4] новым подходом к развитию математического аппарата электродинамики в направлении более адекватного описания перехода от одной инерциальной системы отсчета к другой на основе гиперконтинуальных представлений о пространстве и времени там же разработаны глобально и локально транскоординатные дифференциальные уравнения электродинамики, использующие новые галилееву и транскоординатную производные полевых функций. Так, дифференциальная форма уравнений Максвелла в транскоординатном представлении являет собой следующую систему четырех новых глобально транскоординатных дифференциальных уравнений электродинамики:
![]() ;
; ![]() ; (8)
; (8)
![]() ;
;
![]() , (9)
, (9)
где ![]() ,
, ![]() – производные Галилея полевых функций, выражаемые через частные производные по времени и конвективные производные тех же полевых функций в лабораторной системе отсчета следующими равенствами:
– производные Галилея полевых функций, выражаемые через частные производные по времени и конвективные производные тех же полевых функций в лабораторной системе отсчета следующими равенствами:
![]() ; (10)
; (10)
![]() . (11)
. (11)
Глобальность транскоординатности, обеспечиваемая использованием галилеевой производной, означает, что связываемые дифференциальными уравнениями инерциальные системы отсчета (лабораторная и субстанциональная) могут двигаться друг относительно друга с произвольной, а не только бесконечно малой, скоростью v. При v = 0 (8)–(9) переходит в (7).
В частном случае отсутствия свободных зарядов и токов уравнения (8)-(9) примут вид:
![]() ;
; ![]() ;
; ![]() ;
; ![]() . (12)
. (12)
При ![]() (12) переходит в следующую общеизвестную систему уравнений Максвелла:
(12) переходит в следующую общеизвестную систему уравнений Максвелла:
![]() ;
; ![]() ;
; ![]() ;
; ![]() . (13)
. (13)
Конвективные производные полевых функций в (10)-(11) можно записать в виде:
![]() ; (14)
; (14)
![]() . (15)
. (15)
В силу первых двух уравнений (12) с учетом (1)-(2) имеем:
![]() ;
; ![]() . (16)
. (16)
Подставив (16) в (14)-(15), получим равенства для конвективных производных:
![]() ; (17)
; (17)
![]() . (18)
. (18)
После подстановки (17)-(18) в (10)-(11) имеем другой вид галилеевых производных:
![]() ; (19)
; (19)
![]() . (20)
. (20)
Подстановка галилеевых производных (19)-(20) в последние два равенства (12) дает:
![]() ; (21)
; (21)
![]() . (22)
. (22)
Подставив последние два уравнения (13) в (21)-(22), получим:
![]() ; (23)
; (23)
![]() . (24)
. (24)
Опустим операцию ротора в обеих частях равенств (23)-(24):
![]() ; (25)
; (25)
![]() . (26)
. (26)
Кроме штрихованной системы отсчета, движущейся относительно лабораторной со скоростью v введем еще относительно подвижную систему отсчета – дважды штрихованную, движущуюся в том же направлении с другой скоростью v + ∆v относительно лабораторной. Тем самым, дважды штрихованная система отсчета движется относительно штрихованной со скоростью ∆v, так что штрихованную систему отсчета можно принять за новую лабораторную (относительно неподвижную), а дважды штрихованную – за новую субстанциональную.
Равенства (25)-(26) для них запишем с учетом замены радиус-вектора r′ на r′′:
![]() ; (27)
; (27)
![]() , (28)
, (28)
Запишем равенства (27)-(28) в следующем виде:
![]() ; (29)
; (29)
![]() . (30)
. (30)
В (29)-(30) величины ![]() ,
, ![]() и
и ![]() ,
, ![]() описывают электромагнитное поле в одной и той же точке пространства (среды), но в разных системах отсчета (штрихованной и дважды штрихованной). В рамках концепции инвариантности поля относительно скорости движения наблюдателя они равны:
описывают электромагнитное поле в одной и той же точке пространства (среды), но в разных системах отсчета (штрихованной и дважды штрихованной). В рамках концепции инвариантности поля относительно скорости движения наблюдателя они равны:
![]() ;
; ![]() , (31)
, (31)
причем равенства (4) и (31) имеют одинаковый физический смысл, но применительно к разным парам систем отсчета. Однако вне рамок указанной концепции при переходе от штрихованной к дважды штрихованной системе отсчета полевая функция в данной точке пространства испытывает приращение, предел отношения которого к ∆v при ∆v → 0 дает впервые введенную в [4] транскоординатную производную полевой функции:
![]() ; (32)
; (32)
![]() . (33)
. (33)
Равенства (29)-(30) при ∆v → 0 с учетом (32)-(32) после замены r’’ на r принимают вид:
![]() ;
;
![]() . (34)
. (34)
Если уравнения (12) являются глобально транскоординатными дифференциальными уравнениями электродинамики для случая изотропной однородной среды без дисперсии в отсутствии свободных зарядов и токов, то уравнения (34) представляют собой локально транскоординатные дифференциальные уравнения электродинамики для того же самого случая. Локальность транскоординатности, обеспечиваемая использованием транскоординатной производной, означает, что связываемые дифференциальными уравнениями инерциальные системы отсчета (условно говоря, штрихованная и дважды штрихованная) движутся друг относительно друга с бесконечно малой скоростью ∆v. Уравнения (34) образуют систему, решая которую, можно получить преобразования электромагнитного поля при переходе из одной инерциальной системы отсчета в другую.
Результаты исследования и их обсуждение
Применим систему уравнений (34) для получения преобразований электромагнитного поля при переходе от лабораторной системы отсчета к субстанциональной.
Опуская аргументы функций, запишем векторные произведения в (34) в виде:
![]()
![]() ; (35)
; (35)
![]()
![]() . (36)
. (36)
С учетом (35)-(36) система уравнений (34) разбивается на две независимые системы из двух уравнений каждая и еще два независимых уравнения:
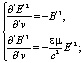
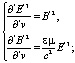
![]() ;
; ![]() (37)
(37)
Продифференцируем первые уравнения систем (37) и подставим их во вторые уравнения:
![]() ;
; ![]() ;
;
![]() ;
; ![]() . (38)
. (38)
Общее решение уравнений (38) выражается через произвольные постоянные ![]() :
:
![]() ;
; ![]() ;
;
![]() ; (39)
; (39)
![]() ;
; ![]() ;
;
![]() . (40)
. (40)
Так как мы ищем преобразования электромагнитного поля при переходе от лабораторной системы отсчета, то искомые частные решения уравнений (38) должны при v = 0 описывать электромагнитное поле в лабораторной системе отсчета, то есть удовлетворять равенствам (3) и (37), а, значит, следующей совокупности равенств:
![]() ;
;
![]() ;
;
![]() ; (41)
; (41)
![]() ;
; ![]() ;
;
![]() ; (42)
; (42)
![]() ;
;
![]() ; (43)
; (43)
![]() ;
;
![]() . (44)
. (44)
Подстановкой (39)-(40) в (41)-(44) найдем значения постоянных ![]() , в результате чего после подстановки этих постоянных в (39)-(40) получим окончательное выражение в компонентной форме для искомых преобразований электромагнитного поля при переходе от лабораторной системы отсчета к субстанциональной:
, в результате чего после подстановки этих постоянных в (39)-(40) получим окончательное выражение в компонентной форме для искомых преобразований электромагнитного поля при переходе от лабораторной системы отсчета к субстанциональной:
![]() ;
;
![]() ; (45)
; (45)
![]() ; (46)
; (46)
![]() ; (47)
; (47)
![]() ; (48)
; (48)
![]() . (49)
. (49)
В векторной форме те же самые преобразования имеют следующий вид:
![]() ; (50)
; (50)
![]() . (51)
. (51)
Легко видеть, что преобразования (45)-(51) есть известные преобразования Менде.
Заключение
Таким образом, преобразования Менде получают достаточное теоретическое обоснование в рамках транскоординатной формулировки электродинамики, связанной с гиперконтинуальными представлениями о пространстве и времени, а также с концепцией не инвариантности электрического заряда относительно скорости движения наблюдателя. Наряду с представленным в [10] прямым экспериментальным подтверждением концепции не инвариантности электрического заряда, это является убедительным свидетельством их большей адекватности физической реальности по сравнению не только с классическими, но и с релятивистскими преобразованиями электромагнитного поля, а также убедительным свидетельством оправданности перевода электродинамики с традиционной формулировки Герца-Хевисайда на транскоординатную. Мы считаем, что последовательное развитие транскоординатной электродинамики способно не только вывести на новый качественный уровень представления о пространстве и времени, но и открыть принципиально новые горизонты развития техники и технологий за счет открытия и освоения новых физических явлений и эффектов.
Библиографическая ссылка
Дубровин А.С. ПРЕОБРАЗОВАНИЯ МЕНДЕ В ТРАНСКООРДИНАТНОЙ ЭЛЕКТРОДИНАМИКЕ // Международный журнал прикладных и фундаментальных исследований. 2015. № 12-6. С. 1006-1012;URL: https://applied-research.ru/ru/article/view?id=8071 (дата обращения: 11.02.2026).

