Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кудряшов А.А. 1 Кытин В.Г. 1 Лунин Р.А. 1 Кульбачинский В.А. 1 Banerjee A. 2

---

1 Московский Государственный Университет имени М.В. Ломоносова

2 University of Calcutta

Исследован эффект Шубникова – де Гааза и эффект Холла в монокристаллах n-Bi2-xTlxSe3(x = 0, 0.01; 0.02; 0.04) и p-Sb2-xTlxTe3 (x = 0; 0.005; 0.015; 0.05). По Фурье-спектрам осцилляций мы рассчитали подвижности носителей заряда и их изменение при легировании Tl в обоих типах материалов. Мы установили, что легирование Tl понижает концентрацию электронов в n-Bi2-xTlxSe3 и увеличивает их подвижность. В p-Sb2-xTlxTe3 и концентрация дырок и их подвижность уменьшается при легировании Tl. В n-Bi2-xTlxSe3 увеличение подвижности электронов указывает на уменьшение концентрации заряженных точечных дефектов при легировании таллием. В p-Sb2-xTlxTe3 концентрация заряженных точечных дефектов, ответственных за начальную высокую концентрацию дырок, понижается в связи с увеличением полярности связей в решетке при замещении сурьмы таллием.

Статья в формате PDF

1641 KB

Эффект Шубникова – де Гааза

подвижности электронов

легирование

1. Janíček P., Drašar Č., Beneš L., andLošťák P. Thermoelectric properties of Tl-doped Bi2Se3 single crystals. Cryst.Res. Technol. – 2009. – Vol. 44. – Р. 505–510.

2. Lošťák P., Novotný R., Horák J. and Klikorka J. Properties of Sb2Te3 single crystals doped with Tl atoms. physica status solidi (a). – 1985. – Vol. 89. – K55-K59.

3. Sher A., Shilon M., and Ben-dor L. The effect of Tl2Te3 on the properties of the solid solution (Sb2Te3)0.75*(Bi2Te3)0.25. J. Electron. Mater. – 1983. – Vol. 12. – № 6. – 983–988.

4. Кульбачинский В.А., Кудряшов А.А., Кытин В.Г. Эффект Шубникова−де Гааза и термоэлектрические свойства Sb2Te3 и Bi2Se3, легированных таллием ФТП. – 2015. – том 49. – вып. 6, 786–792.

5. Kulbachinskii V.A., Kudryashov A.A., Kytin V.G. Influence of Thalliumon the Shubnikov – de Haas effect and Thermoelectric Properties of Sb2Te3andBi2Se3. J. Phys.: CS. – 2014. – Vol. 568. – 052014-1–5.

6. Kul’bachinskii V.A., Kytin V.G., Lunin R.A., Mokerov V.G., Senichkin A.P., Bugaev A.S., Karuzski A.L., Perestoronin A.V.. Transport and optical properties of tin d-doped GaAs structures. Semiconductors.– 1999.– Vol. 33.– №7.– 771-778 (1999).

7. Kulbachinskii V.A., Oveshnikov L.N., Lunin R.A., Yuzeeva N.A., Galiev G.B., Klimov E.A., Pushkarev S.S., Maltsev P.P.. Influence of Buffer-layer Construction and Substrate Orientation on the Electron Mobilities in Metamorphic In0.70Al0.30As/In0.76Ga0.24As/In0.70Al0.30As Structures on GaAs Substrates. Semiconductors.– 2015.– Vol. 49.– №7.- 921-929.

8. Koenraad P.M., van de Stadt A.F.W., Shi J.M., Hai G.Q., Studart N., Vansant P., Peeters F.M., Devreese J.T., Perenboom J.A.A.J., Wolter J.H.. Electron mobility in Si delta doped GaAs.Physica B.– 1995.– Vol.211.– 462-465.

9. Skuras E., Kumar R., Williams R.L., Stradling R.A., Dmochowski J.E., Johnson E.A., Mackinnon A., Harris J.J., Beall R.B., Skierbeszewski C., Singleton J., van der Wel P.J. and Wisniewskiy P. Subband dependent mobilities and carrier saturation mechanisms in thin Si doping layers inGaAs in the high density limit. Semicond. Sci. & Technol.– 1991.– Vol. 6.– 535-546.

10. Kulbachinskii V.A., Miura N., Arimoto H., Ikaida T., Lostak P., Horak H., Drasar C.. Cyclotron Resonance in High Magnetic Fields in Bi2Se3, Bi2Te3 and Sb2Te3 based crystals, J. Phys. Soc. Jap.–1999.– Vol.68.– N10.– 3328-3333.

Теллуриды и селениды висмута и сурьмы являются хорошими термоэлектриками при комнатной температуре, то есть обладают высокой электропроводностью s, низкой теплопроводностью k, высоким значением коэффициента Зеебека S, что приводит к высоким значениям термоэлектрической эффективностью 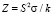. Для получения материалов с высокими значениями Z необходимо исследовать влияние различных факторов, в том числе легирования, на перечисленные величины. Несмотря на интенсивные исследования как теллуридов так и селенидов висмута и сурьмы влияние легирования Tl на их электрофизические и термоэлектрические свойства практически не исследовалось, Есть всего несколько работ по влиянию легирования Tl на свойства Bi2Se3, Sb2Te3 и Sb1.5Bi0.5Te3 [1-5].

В данной работе мы исследовали влияние легирования таллием на полученные из эффекта Шубникова – де Гааза (ШдГ) подвижности носителей зарядав монокристаллах p-Sb2Te3 и n-Bi2Se3.

Образцы

В работе исследованы легированные таллием монокристаллы p-Sb2-xTlxTe3 (x = 0; 0.005; 0.015; 0.05) иn-Bi2-xTlxSe3 (x = 0, 0.01; 0.02; 0.04), полученные методом Бриджмена. При измерениях эффекта Шубникова – де Гааза ток направлялся вдоль оси С2 в базисной плоскости, магнитное поле было направлено перпендикулярно базисной плоскости вдоль оси С3. Измерения эффекта Шубникова – де Гааза проводилось в импульсных магнитных полях до 30-38 Тл при Т = 4.2 К. Концентрация таллия приводится по загрузке при росте монокристаллов. Концентрации носителей тока и энергии Ферми определялись из данных эффекта ШдГ, по методике, описанной в [4,5].Полученные значения следующие: Bi2Se3 (n = 2,2*1019 см-3;EF = 161,7 мэВ), Bi1.99Tl0.01Se3(2,1*1019 см-3; 160,1 мэВ); Bi1.98Tl0.02Se3 (1,9*1019 см-3; 153,4 мэВ); Bi1.96Tl0.04Se3 (1,6*1019 см-3; 140,3 мэВ). Sb2Te3 (n = 2,8*1019 см-3; 97,1 мэВ); Sb1.995Tl0.005Te3(2,7*1019 см-3; 93,7 мэВ); Sb1.985Tl0.015Te3(2,6*1019 см-3; 92,2 мэВ); Sb0.95Tl0.05Te3(1,4*1019 см-3; 61,1 мэВ). Как видно из данных концентрацииэлектронов и дырок, а также энергия Ферми уменьшаются в n-Bi2Se3иp-Sb2Te3при легировании таллием.

Результаты исследования и их обсуждение

Для образцов Bi2-xTlxSe3 (x = 0.01; 0.02; 0.04) эффект Шубникова-де Гааза в сильных магнитных полях также исследовался при ориентации магнитного поля B вдоль оси С3. На рис. 1 приведены осцилляции ШдГ и эффект Холла для исследованных образцов, а на вставке их Фурье-спектры. Во всех образцах наблюдалась только одна частота, что соответствует одному эллипсоиду электронной поверхности Ферми легких электронов в Bi2Se3. Из данных эксперимента по эффекту Шубникова-де-Гааза можно рассчитать концентрацию электронов и энергию Ферми, которые приведены в табл. 1. Методику расчета можно посмотреть в работах [4, 5]. Концентрация электронов и энергия Ферми убывают в Bi2Se3 при легировании Tl.

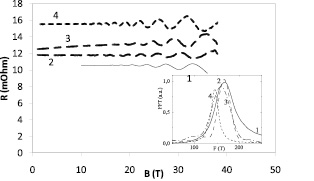
Рис. 1. Осцилляции магнетосопротивления R при Т = 4,2 K образцов 1 – Bi2Se3, 2 – Bi1.99Tl0.01Se3, 3 – Bi1.98Tl0.02Se3 и 4 – Bi1.9Tl0.04Se3(кривые сдвинуты по оси у для наглядности); на вставке их Фурье-спектры

Осцилляции Шубникова-де Гааза для монокристаллов Sb2-xTlxTe3 и их Фурье-спектры приведены на рис. 2. Все измерения были проведены для ориентации магнитного поля вдоль оси С3. В этом случае все сечения 6 эллипсоидов дырочной поверхности Ферми совпадают, и наблюдается только одна частота осцилляций F, что и видно в Фурье-преобразовании, приведенном на вставке рис. 2. Частота осцилляций уменьшается при увеличении легирования, что соответствует уменьшению концентрации легких дырок. По Фурье-анализу найдены частоты осцилляций и определены концентрации легких дырок и энергии Ферми в исследованных образцах.

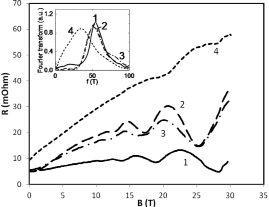
Рис. 2. Осцилляции ШдГ при температуре 4,2 К образцов Sb2-xTlxTe3, x= 1 – 0; 2 – 0.005; 3 – 0.015; 4 – 0.05. На вставке показаны Фурье-спектры соответствующих осцилляций

По эффекту Шубникова – де Гааза можно рассчитать подвижности носителей заряда и их изменения при легировании в Bi2-xTlxSe3 и Sb2-xTlxTe3. При определении подвижностей носителей заряда необходимо различать транспортные и квантовые времена релаксации [6, 7]. Транспортное время релаксации импульса электрона tt определяется средним временем между упругими актами рассеяния на примесях, существенно изменяющих направление импульса, и может быть записано в виде:

(1)

где s(j) пропорционально вероятности рассеяния в единицу времени на угол j. Квантовое время жизни (одночастичное время релаксации) получается при усреднении времени между любыми событиями рассеяния и дается выражением:

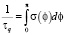(2)

Из-за множителя (1-cosj) в выражении для tt, транспортное время рассеяния может отличаться от квантового. Для изотропного рассеяния, например на фононах, эти времена рассеяния равны. Однако для кулоновского рассеяния на ионизированных примесях s(j) велик при рассеянии на небольшие углы, поэтому tt может быть в несколько раз больше tq.

Анализ зависимости амплитуды осцилляций Шубникова – де Гааза от магнитного поля дает возможность определить квантовые подвижности электронов 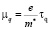. От квантовой подвижности экспоненциально зависит огибающая осцилляций Шубникова – де Гааза [8]:

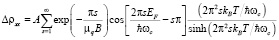(3).

Простейший способ получения квантовой подвижности был предложен в работе [9], в которой показано, что Фурье-спектр первой гармоники осцилляций Шубникова – де Гааза пропорционален следующему выражению:

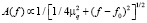, (4)

где mq – квантовая подвижность, а f0 – частота максимума Фурье-спектра. Из формулы (4) следует, что ширина Фурье-пика ∆f (полная ширина на половине высоты) может быть использована для нахождения квантовой подвижности [9]:

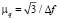. (5)

Ширины Фурье-пиков ∆f для образцов Bi2-xTlxSe3позволили определить квантовые подвижности mq (cm2/Vs) = 340; 520; 360; 930 для х = 0; 0,01; 0,02; 0,04 соответственно и для Sb2-xTlxTe3mq (cm2/Vs) = 1160; 790; 760; 420 для х = 0; 0,005; 0,015; 0,05.

Формула (4) получена в приближении, что температура измерений много меньше температуры Дингла 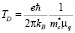, и поэтому последний множитель в формуле (3), содержащий температуру, равен ½. Для исследованных образцов это условие выполнено, так как температура измерений равна 4.2 К, при циклотронной масса электронов для n-Bi2-xTlxSe3 в нижней зоне 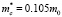22 < 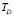< 60 К. Дляp-Sb2-xTlxTe3 циклотронная масса легких дырок в верхней зоне [10], и 23 < 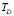< 62 К. Полученное увеличение подвижности объясняется уменьшением заряженных точечных дефектов 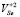, что превалирует над образованием дефектов типа .

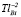Легирование таллием Sb2Te3 приводит в результате к подавлению формирования антиструктурных дефектов 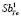(ответственных за высокую начальную концентрацию дырок),что понижает концентрацию дырок и приводит к уменьшению подвижности.

Заключение

Исследован эффект Шубникова – де Гааза и эффект Холла в монокристаллах n-Bi2-xTlxSe3 и p-Sb2-xTlxTe3. Установлено, что легирование таллием понижает концентрацию электронов в n-Bi2-xTlxSe3 и дырок в p-Sb2-xTlxTe3. Подвижности электронов в n-Bi2-xTlxSe3 увеличиваются, а дырок в p-Sb2-xTlxTe3 уменьшаются при легировании Tl.

Работа поддержана РФФИ, грант ИНД-а 15-52-45037.

Библиографическая ссылка