Проектирование микроГЭС проводилось в программе Компас-3Д. Основными задачами при проектирование были:
– доступность технологи при ее изготовлении;
– возможность смены рабочего колеса;
– минимальное количество дополнительного оборудования при монтаже затраты при монтаже монтажа;
– доступность и ремонтопригодность всех узлов.
В результате проведенных расчетов и проработки различных вариантов узлов, была получена следующая конструкция в соответствии с рисунком 1. Устройство работает следующим образом: поток рабочей жидкости с напором через 6 входной раструб поступает в спиральную камеру 1, где происходит работа турбины расположенной в подшипниковым узле 7, скорость и момент через ременную передачу 3 на генератор 2 с повышением частоты вращения. отработанный поток жидкости выходит через расширительный выходной раструб 4. При проектирование предусмотрена выемка подшипникового узла для смены шнековой турбины. Подшипниковый узел вставляется сверху на свои посадочные узлы и закрепляется болтами и на оси закрепляется ведущий шкив.
На раме 5 расположен пазы в которые установлен генератор. Пазы выполнены так чтобы можно производить натяжку ремня. Рама микроГЭС может быть вмонтирована в основани при помощи дополнительных закладных деталей.
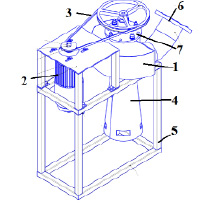
Рис. 1. Общий вид шнековой микроГЭС: 1 – спиральная камера; 2 – электрогенератор; 3 – ременная передача; 4 – выходной расширительный раструб, 5 – рама; 6 – входной раструб; 7 – подшибниковый узел с рабочей турбиной
В работе приведен расчетное обоснование параметров спиральной камеры, на основе методик полученных с применением графоаналитического метода согласно работам Сухоребного П.Н. и Исаева Р.Э., Б.М. Кабланбекова [1, 2].
При расчетном обосновании параметров ставились следующие задачи [3, 4]:
– определить угол f охвата спирального канала для обоснования его геометрических и гидравлических характеристик;
– расчет спиральной камеры определяющий геометрию и обеспечивающий равномерное распределение расхода по всему диаметру направляющего аппарата;
– разработать спиральную камеру, обеспечивающей распределение потока жидкости, которая является потенциальной и обладает осевой симметрией;
– подбор меридионального сечения спиральной камеры так, чтобы обеспечивалось равномерное распределение расхода воды по окружности диаметра направляющего аппарата спиральной камеры.
Структура потока в спиральной части камеры зависит от формы поперечных сечений, угла охвата и принятого закона распределения скорости вдоль спирального канала. Скорость в любой точке потока в спиральной камере состоит из меридиональной Vm и Vu окружной составляющих.
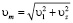 . (1)
. (1)
При рассмотрении движения жидкости и расчете спиральной части камеры обычно принимают следующие допущения:
– поток установившийся и осесимметричный;
– расход через любое сечение спиральной камеры, расположенное в плане под углом φ,
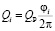 , (2)
, (2)
где Qi – расход через меридиональное сечение спиральной камеры, проведенное под углом φ, QP – расчетный расход через турбину.
Поток в спиральной камере потенциальный, характеризуемый постоянством момента скорости Vu×R= const вдоль спирального канала.
Результирующее движение жидкости в спиральных камерах можно представлено как сумму двух составляющих потенциальных потоков: меридионального потока и циркуляционного потока вокруг оси турбины. Для исследования потока в спиральной камере используем гидродинамическую модель, которая имитирует движение жидкости в спиральной камере при помощи вихревой нити и системы стоков, размещенных на оси турбины. Полагаем, что вихревая нить индуцирует симметричное потенциальное движение жидкости с определенной величиной вращения потока вокруг оси турбины; система стоков характеризует потенциальное симметричное движение, обеспечивающее заданный расход через турбину. Потенциал скорости суммарного потока Ф при этом состоит из потенциала скоростей Фх движения, вызываемого системой стоков, и потенциала скоростей Ф2 движения, вызываемого вихревой нитью.
Гидромеханический расчет турбинной камеры состоит в определении размеров ее поперечных сечений и их углового расположения в плане. Выбор метода расчета зависит от принятых исходных расчетных параметров и характера распределения скоростей вдоль спиральной части камеры. Применяют следующие методы расчета турбинных камер [5, 6]:
– расчет спиральной камеры, основанный на допущении постоянства момента скорости в любой точке потока в спиральном канале (VuR= const);
– проектирование спиральной камеры в предположении, что средняя скорость потока постоянна вдоль спирального канала (Vcp= const);
– расчет турбинной камеры из условия убывания средней окружной скорости вдоль спирального канала;
– определение размеров спирали исходя из принятого изменения направления потока на входных кромках колонн статора и лопаток направляющего аппарата.
В соответствии с рис. 2 приведена расчетная схема рассматриваемой формы спиральной камеры [7, 8, 9]. Из условия равномерности распределения расхода очевидно, что через любое сечение должен пройти расход Qφ, достаточный для питания оставшейся части окружности, определяемый углом φ:
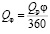 , (3)
, (3)
где Qφ – расход определяемый углом φ; Qp – расчетный расход.
Через входное сечение будет расход:
Qвх=(Qp/360)× φохв. (4)
Определение площади сечения спиральной камеры
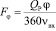 . (5)
. (5)
За площадь сечения камеры следует принимать площадь, ограниченную контуром сечения и входной кромкой направляющего аппарата, расположенной на радиусе rна. Из расчетной модели спиральной камеры можно видеть, что
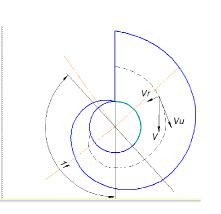
Рис. 2. Расчетная схема спиральной камеры
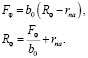 (6)
(6)
Определим рациональное сечение камеры по периметру. При расчете спиральной камеры на основе заданных параметров турбины: мощности N=1000 Вт, расхода Q=17 л/с=0,012 м3/с, напора H=12 м, КПД n=0,68 зададимся минимальной скоростью естественного водотока 2,8 м/с.
Построим входное сечение, удовлетворяющее условию пропуска расхода Qex через это сечение с входной скоростью vвх [10]:
Qвх=(Qp/360)fохв; (7)
Qвх=(0,12/360) 360=0,12 м3/с;
F=Qp×f/(360·vbx)= =0,012·360/(360·2,8)=0,042 м2.
Значение b0 = 0,495 примем как расчетное для определения площади входного сечения спирального канала в соответствии с рис. 3:
b0 D =0,495· 0,1372 = 0,0679 м,
Rf – rна = F/b0 = 0,042/0,0679 = 0,61 м.
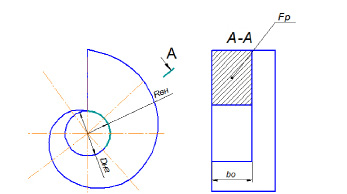
Рис. 3. К расчету спиральной камеры
Используя формулы найдем значения для расчетных углов охвата спиральной камеры через интервал ∆15°.
Применим расчет, основанный на предположении постоянства произведения окружной составляющей скорости vni = vui на радиус Rt в любой точке спиральной камеры, или, как обычно выражаются, – постоянство момента скорости:
vuR = const. (8)
Это выражение является частным случаем постоянства произведения скорости на радиус в осесимметричном потенциальном потоке. Наиболее наглядно это можно показать, когда все скорости направлены по радиусам к центру стока. Тогда из условия сплошного течения несжимаемой идеальной жидкости в плоском горизонтальном слое единичной толщины, расход на окружности радиуса rг можно выразить как
vri 2tcRi = Q, (9)
откуда:
vriRt = Q/(2·pi) = const = C, (10)
так как Q для всех концентричных сечений одинаково.
Гидравлический расчет спиральной камеры по закону vur=const исходит из предположения, что движении жидкости вокруг общей оси при этом общий момент количества движения для каждой элементарной линии величина постоянная, т.е. жидкость при движении по спирали никакой работы не совершает, она лишь получает закрутку в спирали и направляющем аппарате, а закрученный поток воды лишь при поступлении на рабочее колесо изменяет свой момент количества движения, за счет чего и вращается колесо турбины.
В каждой точке потока в спиральной камере скорость воды может быть разложена на две составляющие – радиальную скорость vr, направленную по радиусу к оси турбины, и окружную скорость vu, направленную перпендикулярно к радиусу.
Радиальная скорость будет равна:
Vr=Q/(piDнаb0), (11)
где Q – расход через турбину; Dна – диаметр окружности выходных кромок ребер; b0 – высота направляющего аппарата.
Эта радиальная составляющая скорость должна быть постоянной, чтобы обеспечить равномерное питание направляющего аппарата по всей окружности.
Окружная скорость в любой точке должна подчиняться закону постоянства площадей.
Так как расход через входное сечение спирали Qex известен, а входной скоростью vr;x и формой сечения задаются, то можно определить площадь входного сечения Fex и постоянную спирали.
Определяем постоянную спирали чтобы сохранить вхождения скорости положения в сечений спирали. Для этого в масштабе по вертикали откладываются значения b0/r в зависимости от радиуса R для входного сечения и промежуточных сечений 1, 2, 3, 4,. в соответствии с рис. 4. Результаты расчета сведем в таблицe.
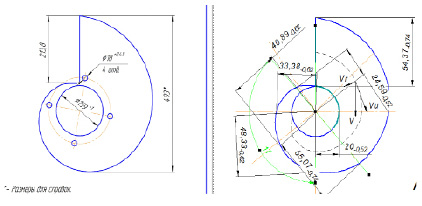
Рис. 4. Конструктивные размеры спиральной камеры: а – размеры спиральной камеры высота спиральной камеры 192 мм; б – закручивание спирали в масштабе (1:4)
Размеры сечений спиральной камеры
|
Сечения |
φ |
Rвн, мм |
Rна, мм |
Rвн–Rна |
|
1 2 3 4 |
150° 120° 90° 60° |
221 193 164 133 |
80 |
141 113 84 53 |
Угол охвата и площадь входного сечения спиральном камеры. Как показывают данные модельных испытаний различных гидротурбин, потери энергии в турбинной камере, статоре и направляющем аппарате зависят (при заданной ширине блока в плане) от соотношения между принятыми площадью входного сечения FBX и углом охвата φ. При выбранных размерах входного сечения спиральной камеры увеличение угла охвата, с одной стороны, приводит к уменьшению неравномерности потока вдоль периметра направляющего аппарата, что благоприятно влияет на характеристики гидротурбин. С другой стороны, при этом увеличиваются скорости. Потери энергии в спиральной камере, статоре и направляющем аппарате уменьшают энергию потока на входе в рабочее колесо и, следовательно, влияют на КПД турбины. Основными потерями энергии в спиральной камере являются потери по длине.
Вывод. В общем случае коэффициент потерь энергии зависит от угла охвата спиральной камеры, изменения средней скорости по длине спирального канала и формы его поперечного сечения. Расчетные и экспериментальные исследования показывают, что величина относительной кинетической энергии в спиральной камере невелика 2~ 4 % и потери энергии в ней незначительны, согласно опытным данным для турбинной камеры трапециевидного вида.
Библиографическая ссылка
Нурдаулеткызы А., Умбетов Е.С., Уткин Л.А. ОБОСНОВАНИЕ ПАРАМЕТРОВ СПИРАЛЬНОЙ КАМЕРЫ МИКРОГЭС СО ШНЕКОВОЙ ТУРБИНОЙ // Международный журнал прикладных и фундаментальных исследований. 2016. № 1-1. С. 14-18;URL: https://applied-research.ru/ru/article/view?id=8284 (дата обращения: 05.01.2026).

