Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чермидов С.И. 1

---

1 ФГБОУ ВПО «Кубанский государственный университет»

В статье на базе множества DCPN распределения параметров составных чисел CN и простых чисел PN (Distribution of Parameters of Composite and Primer Numbers) [1], получено что множество состоит из следующих трёх подмножеств чисел: PPCN – параметров простых и составных чисел; PTw – параметров близнецов простых чисел; PTwCN – параметров чисел близнецов составных чисел отличающихся также друг от друга с той же разностью на 2 (два), что и в Tw. На базе множества DCPN предлагается вариант доказательства бесконечности близнецов составных чисел, а также рассматриваются причины их возникновения. В статье приводится доказательство того факта, что в интервалах между квадратами соседних натуральных чисел, всегда существуют элементы множества θ. Представлен вариант решения гипотезы Лежандра (3-я проблема Ландау), что между квадратами соседних натуральных чисел всегда существуют простые числа. Почти для всех утверждений приведены числовые примеры. На представленные в статье алгоритмы приведены описания и их листинги программ на Software Module ACCESS.

Статья в формате PDF

1724 KB

гипотеза Лежандра (3-я проблема Ландау)

бесконечность близнецов составных чисел в множестве θ

1. Чермидов С.И. (Tsermidis S.I.) Распределение простых чисел. Алгоритм чисел близнецов и их бесконечность // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета (Научный журнал КубГАУ) [Электронный ресурс]. – Краснодар: КубГАУ, 2015. – № 06(110). – С. 414–436. – IDA [article ID]: 1101506028. – Режим доступа: http://ej.kubagro.ru/2015/06/pdf/28.pdf.

2. Минаев B.А. Об интегральных оценках распределения простых чисел // Вестник Российского нового университета. – 2011. – № 4.

3. Колесников Е.Ю. Анализ принципов и законов распределения простых чисел // Вестник Московского государственного университета печати. – 2012. – № 9.

4. Bateman P.T. EWING // Department of Mathematics, http://www.math.uiuc.edu/~berndt/hundred-years-of-prime-numbers.pdf.

5. Drushinin V.V. The proof for hypothesis of Legendre existence of a prime between two squares // Austrian journal of Technical and Natural Sciences. – 2014. – № 7–8.

6. Прахар К. Распределение простых чисел / пер. с нем. А.А. Карацуба, под ред. А.И. Виноградова. – М.: МИР. 1967.

7. Шыхалиев Л.А. Решение 3-й проблемы Ландау // Открытые математические проблемы.

Значительна простых чисел как в самой математике так и далеко за её пределами. Например, во второй половине 20-го века они находят практическое применение в криптографии для засекречивания важной военной информации, для защиты информации крупных компаний, в навигации, в кодировании и т.д.

Задача распределения простых чисел [6] в натуральном ряду до сих пор является нерешенной. Известные математики в прошлом [4], предлагали ряд теорий и гипотез, для того чтобы приблизиться к закономерностям их распределения. Поэтому распределения простых чисел до сих пор является актуальной значимой задачей.

В списке перечисленных проблем немецкого математика Ландау представлена, так называемая гипотеза Лежандра (hypothesis Legendre), в которой сказано следующее: «Верно ли, что между квадратами любых соседних натуральных чисел всегда существует хоть одно простое число».

Из работ Д. Гильберта известно, что для решения аддитивных проблем в теории чисел, необходимо знать закон распределения простых чисел. Ссылаясь на полученный автором метод распределения параметров составных чисел CN и простых чисел PN (Distribution of parameters of Composite and Primer Numbers – DCPN) [1] на базе элементов множества θ заметим, что кроме простых чисел близнецов (twins of prime numbers – Tw) существуют и близнецы составных чисел (twins of composite numbers – TwCN), также отличающиеся друг от друга с разницей на 2 (два) как и при простых числах близнецов.

Целью данной работы является определение и причины возникновения чисел TwCN, доказательство их бесконечности и решение гипотезы Лежандра (3-й проблемы Ландау) hypothesis A Legendre (3rd problem E. Landau).

Краткий современный обзор по проблеме Лежандра

В последнее время в работах учёных математиков для доказательства гипотезы Лежандра прослеживаются схожие методы и подходы, которые сводятся либо к решению гипотезы Римана о нетривиальных нулях дзета функции ζ(s), либо к постулату Бертрана [7], либо алгоритму Эратосфена [5], либо на неравенство Лежандра 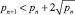(где pn – n-е простое число), которое, кстати, само до сих пор не доказано, хотя Хохайзель в 1930 г. показал, что существует такое число α < 1, для которого 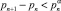[6].

В статье [2] В.А. Минаева приведено доказательство гипотезы Лежандра на базе чисел множества θ = {6k ± 1/k ∈ N} путём подсчета простых чисел π(χ) и составных чисел c(χ) в интервалах, с применением ассимптотического закона распределения, что влечет громоздкость и трудности в рассуждениях из-за неточности количества простых чисел определенных функцией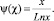

В работе [3] Е.Ю. Колесникова вводится обозначение NP для чисел не делящихся на данное простое число p и вычеркиваются все те числа делящиеся на p, затем для следующего p и т.д. Доказывается, что на интервале 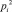до 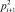все числа NPi являются простыми числами и по аналогии решается проблема Лежандра. Однако, в выводах подчеркивается, что порой с высокой точностью совпадают распределения простых чисел, а с другой стороны говорится, что они появляются на числовой оси как «трава в лесу».

В статье Л.А. Шыхалиева [8] даются доказательства проблем Брокарда и Лежандра, основываясь на постулате Бертрана. В своем исследовании автор рассматривает вариант решета Эратосфена зафиксировав простое число pn. Все натуральные числа от 1 до 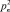, записывает в виде квадратной таблицы размера pn×pn и вычёркивает числа кратные соответственно по простым числам p1, p2, p3, ..., pn ..., а затем утверждает о наличие простого числа в интервалах 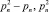, где p1 = 2; p2 = 3... pn ... Таким образом, данная проблема до сих пор не решена.

Определение близнецов составных чисел в множестве DCPN

Рассмотрим примеры составных чисел близнецов:

TwCN20 = (119; 121);

TwCN24 = (143; 145);

TwCN36 = 6∙36 ± 1 = (215; 217);

TwCN41 = (245; 247);

TwCN54 = 6∙54 m 1 = (323; 325);

TwCN57 = 6∙57 ± 1 = (341; 343);

TwCN79 = 6∙79 ± 1 = (473; 475);

TwCN111 = 6∙111 ± 1 = (665; 667);

TwCN116 = 6∙116 ± 1 = (695; 697);

TwCN134 = (803; 805);

TwCN196 = (1175; 1177), ...

Индекс i указывает на параметр числа 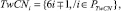где PTwCN есть множество параметров TwCN (см. ниже).

Способ определения близнецов составных чисел в множестве DCPN

Как приведено в [1], параметры 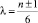∀ составного n ∈ θ, представимы одним из следующих функций (1), где x, y, λ ∈ N

1.

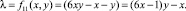
2.

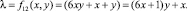
3. 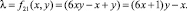(1)

4.

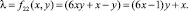
Функции (1) возрастающие по обоим направлениям переменных (x, y) [1].

Первое и второе выражения (1) соответствуют составным и простым числам вида 6λ + 1.

Третье и четвертое выражения (1) соответствуют составным и простым числам 6λ – 1.

Множество значений функций (1) являются счетными и бесконечными.

Счетными являются и параметры всех составных чисел (FN) в множестве θ, где

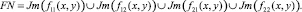
Счетными также являются множества составных чисел разделенные по подкатегориям CN+ и CN– по видам:

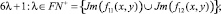
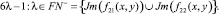
Структура множества DCPN

В таблице [1], показано что элементами множества DCPN являются все натуральные числа разделённые на два столбца с пометками «+» или «–», где плюсы соответствуют к простым числам и минусы к составным числам согласно функционированию форм: 6∙id + 1 по первому столбцу и 6∙id – 1 ко второму столбцу.

Пусть PCN – параметры составных чисел и PPN – параметры простых чисел.

Тогда множество DCPN распадается на параметры трёх следующих подмножеств:

1. PPCN – параметры PCN ∪ PPN, т.е. 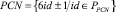id: «±», «m».

2. PTw – параметры простых чисел близнецов 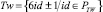id: «+», «+».

3. PTwCN – параметры составных чисел близнецов 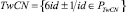id: «–», «–».

Здесь видно по пометкам параметров id, что PTw ⊂ PPN и PTwCN ⊂ PCN.

Исследование причин возникновения чисел TwCN

Обозначим α1, α2, α3, α4, α5, α6 соответственно для каждого из ниже следующих Диофантовых уравнений (2), множества чисел для которых значения функций fi,j(x, y), i ≤ 2, j ≤ 2 совпадают при различных переменных (x, y) и (x′, y′):

1.

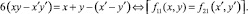
2.

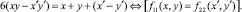
3. 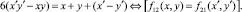(2)

4.

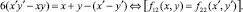
5.

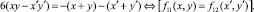
6.

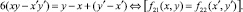
Эти множества и являются строительными блоками представлений параметров чисел TwCN, например:

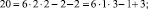
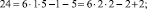
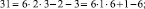
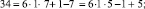
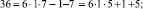
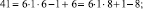
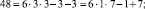
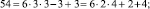
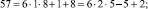
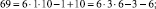
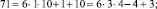
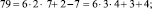
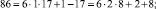
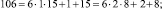
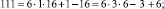
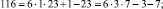
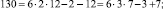
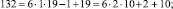
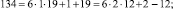
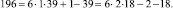
Следовательно, объединение PTwCN = α1 ∪ α2 ∪ α3 ∪ α4 ∪ α5 ∪ α6, есть полная перечень параметров для чисел TwCN в множестве DCPN.

Бесконечность близнецов составных чисел в множестве DCPN

Параметры чисел TwCN лежат на не пустых пересечениях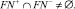

Для доказательства бесконечности чисел TwCN, рассмотрим таблицу малой размерности 10×10, которой могут отсутствовать какие-либо параметры TwCN, так как значения функций в некоторых сочетаниях переменных x, y отсутствуют, поэтому чем больше размерность таблицы m×m тем полнее последовательность параметров TwCN.

Пусть

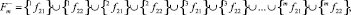
где слева в верхнем углу индексы значений функций (1) по x = 1, 2, 3, ..., m.

При m = 10, имеем таблицу.

Формирование параметров составных чисел в множестве θ

Теорема 1. Множество близнецов составных чисел в множестве θ бесконечно.

Доказательство бесконечности близнецов составных чисел проведём методом математической индукции, построив базу индукции из последовательностей βi. Пусть

1.

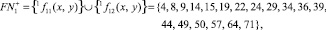
пусть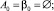

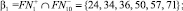
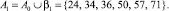
2.

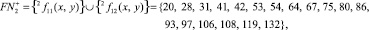
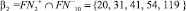
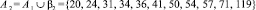
3.

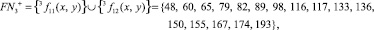
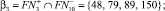
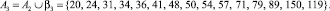
4.

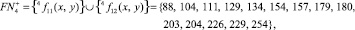
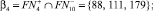
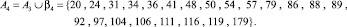
5.

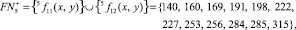
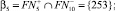
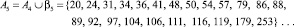
Пусть выполняется выше изложенный процесс до βn Допустим βn+1 = ∅, то в силу того, что элементы βi синтезируются из чисел находящиеся на пересечениях счетных множеств 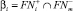следует, что функции (1) должны быть ограниченными, невозрастающими чего быть не может, ибо функции (1) бесконечные и возрастающие, следовательно из противоречия следует, что βn+1 ≠ ∅, а значит и найдется последовательность βn+1.

Таким образом, построено счетное множество 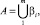, где m → ∞ и так как параметры чисел TwCN после формирования множеств 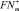и 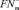все различные (в силу операции объединения), значит и различные сами числа TwCN. Так как любое счетное множество с различными элементами является бесконечным, то множество параметров PTwCN является бесконечным, а значит бесконечны и сами числа TwCN ЧТД.

Предложение 1. В интервалах между квадратами соседних натуральных чисел всегда существуют элементы множества θ.

Доказательство. Рассмотрим разность между квадратами соседних натуральных чисел,

(n + 1)2 – n2 = 2n + 1.

Пусть n = 3k, тогда имеем числа вида n = 6k + 1 если n = 3k – 1 получим числа вида n = 6k – 1, следовательно, в интервалах n2...(n + 1)2 всегда содержится хотя бы один элемент из множества θ. Пусть n2 < 6k + 1 < (n + 1)2 и n2 < 6k – 1 < (n + 1)2, тогда имеем интервал k изменений параметров, которые находятся по следующим неравенствам:

a)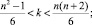

b) 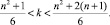(3)

Пример 1. Пусть n = 7, имеем интервал49–64. Найдем интервал k из неравенства (3α), имеем < k < 11 → k = {9, 10}, значит, элементы θ в этом интервале будут

6∙9 ± 1 = (53; 55)

и

6∙10 ± 1 = (59; 61) → {49, 53, 55, 59, 61, 64}.

Теорема 2 (Лежандра). ∀n ∈ N в интервале n2...(n + 1)2 всегда найдётся простое число

Доказательство. Так как параметры PTwCN лежат на не пустых пересечениях решений

Диофантовых уравнений (1).

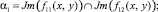
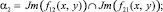
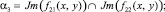
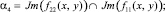
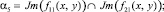
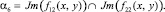
И поскольку каждое множество пересечений по определению ≤ самого множества, имеем следующие неравенства:

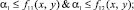
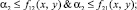
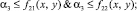
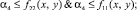
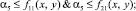
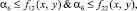
тогда почленно объединяя их имеем:

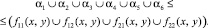(4)

И учитывая, что при изменении областей определения параметра λ, значения форм 6λ ± 1 принимают различные типы множеств, например:

ξ1) 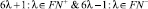являются составными числами в θ;

ξ2) 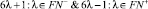являются простыми числами в силу Предложения 2 [1], (т.к. при изменении областей определений соответственно в формах.

Диофантовые уравнения (1) не имеют решений. Объединив всех параметров λ из ξ1) и ξ2) получаем, что PPCN есть PCN ∪ PPN, следовательно,

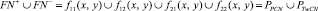
тогда из (4) следует, что

,

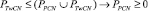но так как параметры DCPN являются последовательностями натуральных чисел и состоят из объединений PPCN ∪ PTw ∪ PTwCN, то еще больше усиливается неравенство PPCN ≥ 0, т.е. PPCN ∪ PTw > 0, следовательно, в полученном интервале k из 3α следует, что всегда существуют элементы параметров множеств PCN или Tw и поскольку в параметрах PPCN и PTw всегда содержится знак плюс «+», то наличие простых чисел гарантируется, а значит и гипотеза А. Лежандра (3-я проблема Э. Ландау) становится справедливой, ЧТД.

Пример 2. При n = 11 имеем n2 = 121, (n + 1)2 = 144, найдём максимальный интервал изменений параметров k из

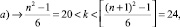
следовательно, k = {21, 22, 23}.

Отметим, что в таблице

id = 21: «+», «–» ∈ PPCN;

id = 22: «–», «+» ∈ PPCN

и

id = 23: «+», «+» ∈ PTw,

тогда имеем последовательность элементов θ в интервале

k: {121, 125, 127, 131, 133, 137, 139, 144},

где {121, 131, 137, 139,} ∈ P.

Пример 3. Пусть n = 318, найдем интервал n2 = 10112,4 – (n + 1)2 = 101761.

Найдём максимальныйй интервал k из a):

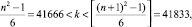
тогда в интервале k число элементов θ, будет

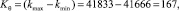
количество параметров KTw и KTwCN найдём алгоритмически, путём подсчета чисел в DCPN соответственно по признакам для Tw: «+», «+» и для TwCN TwCN: «–», «–», KTwCN = 54; KTw = 6, тогда количество параметров

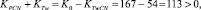
значит существуют простые числа в интервале k.

Перечень параметров TwCN в интервале 41666 < k < 41833:

16854 – 16855 – 16856 – 16859 – 16861 – 16863 – 16865 – 16869 – 16871 – 16872 – –16873 – 16874 – 16875 – 16876 – 16877 – 16883 – 16884 – 16885 – 16886 – 16888 – –16892 – 16895 – 16898 – 16899 – 16901 – 16904 – 16906 – 16907 – 16909 – 16910 – –16912 – 16916 – 16918 – 16920 – 16924 – 16925 – 16926 – 16928 – 16931 – 16932 – –16936 – 16937 – 16939 – 16941 – 16943 – 16945 – 16946 – 16948 – 16951 – ...

Нахождение параметров id для чисел TwCN по переменным (x, y)&(x′, y′) легче найти по программе, чем решать Диофантовые уравнения (2).

Описание программы ParamTwCN

Вводится параметр числа TwCN в поле <Π2>, также заносится в поле <sk> вариант с которой мы хотим найти решения (i, j). Диофантовых уравнений (2), проверяются в цикле все значения функций (1) на равенство с значением поля <Π2>, если нет таких (i, j), значит, число в поле <Π2> не является параметром TwCN.

Описание программы TwCN

Количество пар TwCN на участке (1 – N).

Вводится натуральное число в поле <Π2> , т.к. параметры чисел TwCN в шесть раз меньше, то поиск параметров этих чисел начинается с 1 до Π2\6. Программой PFA(TwCN1,ss) проверяются сгенерированные числа 6i + 1 и 6i – 1 самой программой.

На TwCN и если оба числа имеют минус «–», то идет подсчет близнецов составных чисел, иначе не увеличивается на единицу и переходит к следующему шагу генерации.

Заключение

В работе введено новое понятие – числа близнецы составных чисел (TwCN).

Представлен способ получения и доказательство их бесконечности, а также дано описание и алгоритм нахождения чисел TwCN. Дано доказательство существования простых чисел в интервале между квадратами соседних натуральных чисел.

Библиографическая ссылка