Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Умбетов Е.С. 1 Уткин Л.А. 1 Омаров Р.А. 2 Осмонов Ы.Д 3 Шоколакова Ш.К. 1

---

1 Некоммерческое акционерное общество «Алматинский университет энергетики и связи»

2 Научно-исследовательский институт электрификации и и механизации сельского хозяйства

3 Кыргызский национальный аграрный университет, Бишкек

Настоящая статья посвящена методу трехмерного гидродинамического моделирования, для оптимизации параметров микроГЭС, с использованием программного продукта FlowVision-HPC для вариантного анализа объемно-шнекового профиля четырех и пяти лопастной гидротурбины.

Статья в формате PDF

1000 KB

трехмерное гидродинамическое моделирование

вариантный анализ

шнековая гидротурбина

микрогэс

1. Викторов Г.В. Трехмерная задача для решеток лопастей гидромашин // Тр. МЭИ. – 1972. – Вып. 132. – С. 66–79.

2. ANSYS CFX-Solver Theory Guide. Release 14.5. October 2012. ANSYS CFX-Solver Modeling Guide. Release 14.5. October 2012.

3. Домбровский В.В., Коломейцева М.Б., Орахелашвили Б.М. Моделирование гидроэнергетических процессов малой ГЭС для задачи управления частотой гидроагрегата // Электрические станции. – 2002. – № 2. – С. 37–44

4. Лямасов А.К. Исследование работы гидромашин малой ГЭС: центробежного насоса в обращенном режиме и гидродинамической передачи // Вестник УГАТУ. – 2013. – Т. 17. – № 3 (56). – С. 189–193.

5. Лямасов А.К., Орахелашвили Б.М. Исследование работы обращенных центробежных насосов в качестве турбин малых ГЭС // Труды второй Всероссийской научно-практической конференции Повышение надежности и эффективности эксплуатации электрических станций и энергетических систем «Энерго-2012». – М.: Издательский дом МЭИ, 2012. – С. 377–380.

6. Белов И.А., Исаев С.А. Моделирование турбулентных течений: учебное пособие. – СПб.: Балт. гос. техн. ун-т, 2001. – 108 с.

В настоящее время применение методов математического моделирования обтекания лопастных решеток и иных элементов конструкций микроГЭС и определения их характеристик, является актуальным. Такая методика позволяет не только провести оптимизацию проектируемого объекта, но и значительно уменьшить объемы дорогостоящих экспериментальных исследований. Конечно, проведение модельных или натурных испытаний необходимо для подтверждения результатов численного моделирования.

Для рационального проектирования новых гидротурбин необходимо знать характеристики пространственного течения во всех элементах проточной части.

Нами представлен для трехмерного моделирования новая конструкция объемно-шнековой гидротурбины адаптированной к идеальному процессу пространственного течения жидкости.

Предлагаемая шнековая гидротурбина состоит условно из трех частей в котором учитываются все процессы объемного течения жидкости, в частности:

– режим входа в гидротурбину, т.е. изначально течение имеет вращательное течение, обусловленным углом наклона направляющих, соответственно верхняя часть турбины выполнена виде спиральной камеры;

– режим плавного перехода для ускорения турбины, т.е. течение полностью подготавливается к переходу от потенциальной энергии в кинетическую энергию;

– режим закрутки, т.е. острый угол турбины полностью ускоряет вращательный момент.

Известно работы, в которых исследование трехмерного обтекания проточной части проводилось различными программными комплексами, которые имеют ряд особенностей FlowVision-HPC [1, 2, 3]. На основе известных методик [4, 5] нами предложен алгоритм трехмерного моделирования шнековой турбины:

1. Постановка задачи, задание цели моделирования, выбор расчетной области с подготовкой геометрии модели.

2. Наложение на геометрическую модель сетки контрольных объемов.

3. Задание условий моделирования (свойств вещества, граничных условий).

4. Построение расчетной сетки.

5. Получение результатов гидродинамического расчета.

На основании имеющихся чертежей в Flowvision создаем эскиз меридионального сечения лопастных систем в соответствии с рис. 1, а. При этом необходимо определить положение втулки, периферии, входа, выхода, а также входной и выходной кромок.

В качестве исходных данных для получения геометрии лопасти необходимо задать углы входа и выхода лопасти на втулке и периферии, количество лопастей, а также распределение толщины по длине лопасти. Данные берем из проведенного ранее расчета и составляем расчетные сегменты в соответствии с рис. 1, б.

Использование модели сегмента лопастной системы значительно сокращает время расчета и необходимые вычислительные ресурсы, поскольку качественная сетка имеет гораздо меньшее количество узлов.

Как было сказано ранее на основании созданной ранее геометрии сетка контрольных объемов накладывается в программе Flowvion в соответствии с рис. 1.

Создание сетки можно условно разделить на два этапа:

– разбиение на элементы всей области системы;

– создание сетки пограничного слоя.

Некоторые параметры качества сетки можно отслеживать сразу при ее получении, основываясь на рекомендациях разработчика ПО. В результате, получены следующие сетки контрольных объемов:

Как видно из представленных рисунков основной объем системы разбит тетра (thetra) сеткой, а пограничный слой – гекса (hexa) сеткой. Подобное наложение сетки контрольных объемов позволяет рассчитать пограничный слой и одновременно с этим быстро рассчитать остальной поток.

Создаем граничные условия, которые ограничены граничными поверхностями, которые соответствуют внешним стенкам шнековой турбины и шнековой спирали. На соответствии с рис. 2 показано разбиение на поверхности.

Также необходимо задать скорость и направления вращения турбины.

При расчете использовалась следующая плотность разбиения 158 000 узлов.

В качестве рабочей жидкости принята вода из стандартной библиотеки Ansys, для которой характерны следующие параметры: плотность 997,0 кг/м3, молярная масса 18,02 г/моль, температура 25 °С, удельная теплоемкость 4181,7 Дж/кг·К.

Кроме того для каждой лопастной системы необходимо задать граничные условия, которые назначаем исходя из рекомендаций и программы условий работы. Представим граничные условия, используемые для расчета, в следующей табл. 1.

Интерфейс периодичности устанавливается на поверхности, полученные в результате образования сегмента с целью замыкания расчета по всей области течения. Конкретные численные значения граничных условий согласно табл. 1 устанавливаются в зависимости от расчетного режима с учетом логики вычислений.

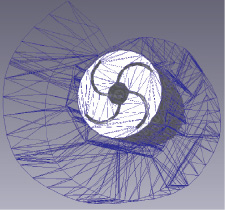
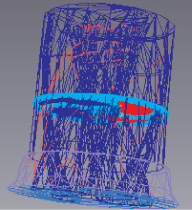
а б

Рис. 1. Сетка контрольных объемов: а – спиральная камера; б – шнековая турбина

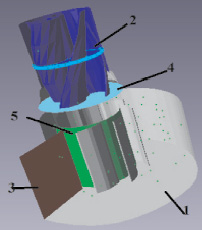
Рис. 2. Структура геометрии граничных поверхностей: 1 – серый цвет – неподвижные стенки; 2 – синий цвет – вращающие поверхности; 3 – красный цвет – поверхность входа потока жидкости; 4 – голубой цвет -поверхность выхода потока жидкости; 5 – зеленый цвет – скользящая поверхность (осуществляет связь между шнекоми спиралью)

Таблица 1

Структура параметров граничных условий

При моделировании применяется стандартная модель турбулентности k-ε (существует также RNG и realizable k-ε модели). Данная модель является наиболее предпочтительной в большинстве технических расчетов, поскольку она позволяет получить результат удовлетворительной точности (достаточно хорошо согласующийся с физическим экспериментом) при разумных временных затратах. Данная модель является полуэмпирической и построенной в предположении о реализации полностью развитых турбулентных течений при больших числах Рейнольдса [6].

В Flowvision стандартная модель турбулентности описывается следующим образом.

Кинетическая энергия турбулентности и скорость диссипации кинетической энергии могут быть получены из следующих уравнений переноса:

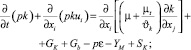(1)

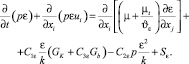(2)

Таким образом, часть пограничного слоя вблизи стенки при использовании модели турбулентности k-ε описывается эмпирической функцией с эмпирическими коэффициентами. Рекомендуется, чтобы значение y+ на твердой стенке составляло не более 300. То есть, практически весь профиль скорости вблизи стенки аппроксимируется эмпирическим соотношением, что отражается на точности моделирования пограничного слоя.

Существуют модели турбулентности, которые позволяют смоделировать эпюру скорости вблизи стенки без использования пристеночных функций. К таким моделям относятся модели k-, SST и прочие модели на их основе. Эти модели позволяют получить более точные решения, однако для их корректного использования необходимо расчетную область вблизи стенки разбивать на сетку. Поскольку толщина пограничного слоя, как правило, составляет очень маленькое значение и поэтому необходимо использовать крайне густую сетку. Получить решение для столь густых сеток способны лишь специальные расчетные станции или кластеры на базе самых современных вычислительных машин.

Геометрия изменялась в результате проведенных расчетов с целью повышения эффективности. Анализ проводился по эпюрам распределения скоростей и давлений, представленных в соответствии с рис. 3–4 а также по интегральным показателям лопастных систем на входе и выходе расчетных областей.

В поле распределения скоростей показано турбулентное перемещение потока в рабочей части, поле распределение давления показано неравномерность загрузки всех лопаток – это вызвано малым их количеством, что приводит к срыву потока скорости вследствие чего появлению турбулентности. Интегральные значения параметров лопастных систем сведем в следующую табл. 2.

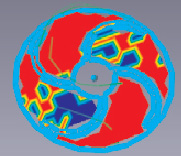
а б

Рис. 3. Поле распределения параметров в динамике в FlowVision: а – абсолютная скорость; б – давления лопасти

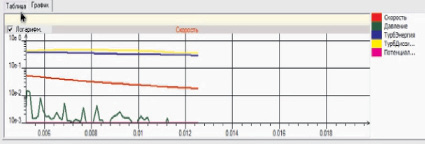
Рис. 4. График распределения абсолютной скорости и давления лопасти в программе FlowVision

Таблица 2

Интегральные значения параметров лопастных систем

Как видно из табл. 2, полученные лопастные системы с достаточной степенью точности согласуются между собой в расчетной точке, чем доказывается принципиальная возможность создания шнековой турбины. По полученным результатам можно рассчитать изменения геометрических параметров лопастных решеток.

Таким образом, применение метода трехмерного гидродинамического моделирования позволило выбрать оптимальную геометрию потока и лопастной системы, а также наметило пути изменения лопасти шнековой турбины, обеспечивающих высокую эффективность.

Выводы

1. На основе программного продукта FlowVision-HPC составлен алгоритм трехмерного моделирования.

2. Общая структура гидродинамического расчета начата с подготовки геометрии расчетной модели. Реализация проведена с помощью программного пакета ANSIS CFX-5, в котором по полученным поверхностям были созданы твердые тела, что существенно упростило импортирование модели в среду FlowVision-HPC.

3. В результате проведения трехмерного гидродинамического моделирования для различных расходов при заданной частоте вращения на входе в лопастную решетку были получены данные для построения энергетических характеристик шнековой турбины.

Библиографическая ссылка