Использование вибровозбудителей планетарного типа в дорожном строительстве является одним из эффективных методов повышения производительности уплотняющих машин. Широко исследованы и применяются на практике симметричные планетарные вибровозбудители, центр вращения которых совпадает с центром кривизны круговой беговой дорожки [1], но практически не исследованы планетарные вибровозбудители с некруглой (комбинированной) беговой дорожкой [2]. В инженерной практике требуется, чтобы в местах соединения непрерывные коники были не только гладкими, но и плавными.
Цель исследования – определение условий безударного соединения комбинированной беговой дорожки планетарного вибровозбудителя, установленного в вальцах дорожных катков и взаимодействующие с уплотняемой средой.
Материалы и методы исследования
Для исследования рассматривается математическая модель планетарного вибровозбудителя с комбинированной формой беговой дорожки и методика аналитического исследования с применением аппарата дифференциальной и аналитической геометрии.
Результаты исследования и их обсуждение
Рассмотрим АПВ с беговой дорожкой, составленной из полудуг окружности радиуса a и эллипса с полуоями a и b, форма которых описываются уравнениями x2 + y2 = a2 и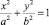 
соответственно. Точки соединения P(a, 0) и P′(–a, 0) расположены вдоль горизонтальной оси Ox (рис. 1, а).
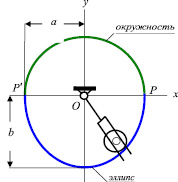
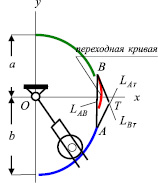
Рис. 1. Вибровозбудитель с комбинированной беговой дорожкой
Окружность является кривой, радиус кривизны которой в любой точке одинаков и равен радиусу самой окружности, т.е. ρ = a, а для эллипса радиус кривизны в любой точке вычисляется по формуле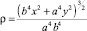 
и является кривой с изменяющимся радиусом кривизны.
Например, если комбинировать беговую дорожку из полудуг окружности x2 + y2 = 122 и эллипса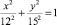 
, то радиусы кривизны в точке P(12, 0) равны: для окружности ρok = 12, для эллипса ρэл = 18,75. Аналогичные радиусы кривизны в точке P′(–12, 0).
Таким образом, в случае соединения дуги эллипса с дугой окружности с радиусом, равным одному из полуосей, точка соединения имеет общую касательную, но имеет скачок по кривизне.
Инерционный элемент вибровозбудителя совершает движение по комбинированной беговой дорожке, составленной из дуг коник с общей касательной в точках соединения. При переходе из одной части в другую, в точках соединения возникает разрыв кривизны, вызывающий скачок центробежной силы. Для того, чтобы обеспечить переход без скачка необходимо между ними вставить переходный участок в виде дуги кривой, удовлетворяющей условиям (рис. 1, б):
а) дуга должна проходит через точки соединения A и B;
б) соединяющая и соединяемая части должны имет одинаковую непрерывную первую производную в точках соединения (в этой точке скорости должны быть равными);
в) соединяющая и соединяемая части должны имет одинаковую непрерывную вторую производную в точках соединения (в этой точке радиусы кривизны должны быть равными);
Применяя метод Лайминга [3] можно получить аналитическое выражение соединяющей коники, имеющее две заданные касательные в двух точках и проходящее через третью точку в виде
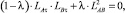(1)
Уравнение (1) представляет пучок конических сечений, проходящих через точки A и B, здесь прямая LAτ = 0 является касательной в точке A, а прямая LBτ = 0 – касательной в точке B, прямая LAB = 0 – хордой, соединяющей точки A и B.
Параметр λ, определяется заданием точки M, если точка M имеет координаты xM и yM, тогда
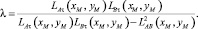
Следовательно, кривая переходного участка беговой дорожки определяется: двумя точками соединения – точками касания A и B; точкой пересечения касательных T; некоторой точкой M. Выбирая точку M внутри базисного треугольника ΔATB определяем непрерывную кривую первого порядка гладкости между точками соединения A и B.
На рис. 2, а представлены несколько вариантов коник переходного участка. Все коники удовлетворяют условиям непрерывности и касания, но в точках A и B имеют различные радиусы кривизны. Дуги внутри базисного треугольника будут гладкими.
Выбирая параметр λ в уравнений (1) определенным образом, можно получить форму кривой, удовлетворящую условию плавности, а именно, полученная методом Лайминга коника в точках соединения A и B должна иметь радиусы кривизны, равные заданным радиусам кривизны ρA и ρB.
Найдем условия, обеспечивающие непрерывность по кривизне и установим некоторые опорные закономерности.
Возьмем две точки A(xA, yA) и B(xB, yB) на эллипсе с радиусами кривизны ρA и ρB соответственно и проводим через них касательные LAτ и LBτ. Касательные LAτ и LBτ взаимно пересекаются в точке T. Соединив точки A, B и T получаем базисный треугольник ΔATT, составленный из касательных LAτ, LBτ и хорды LAB. TC медиана базисного треугольника.
Обозначим через lA = AE, lB = BE – длины отрезков касательных LAτ и LBτ до их пересечения в точке T, dA = OAd, dB = OBd – расстояния от центра O до касательных LAτ и LBτ, hA = AAh, hB = BBh – расстояния точек A и B до касательных LBτ и LAτ, α = ∠BAT, β = ∠ABT – углы между касательными LAτ, LBτ и хордой AB, αE = ∠ATT, βE = ∠BTT – углы между касательными LAτ, LBτ и медианой TC.
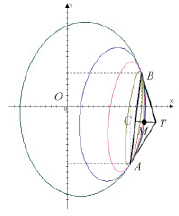
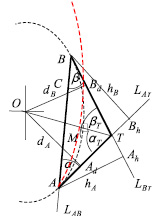
Рис. 2. Кривые Лайминга первого порядка и базисный треугольник
Известно, что радиус кривизны эллипса обратно пропорционален кубу расстояния от центра до касательной в соответствующей точке [4], то есть:
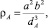
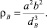
Используя их введем безразмерный коэффициент
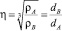
и назовем коэффициентом отношения радиусов кривизны.
Введенный таким образом коэффициент η в дальнейшем будет играть определяющий роль для нахождения места плавного соединения.
Четыре точки: центр эллипса O, точки основания перпендикуляров Ad и Bd и точка пересечения касательных T находятся на одной окружности (окружность пересечения) [5]. Рассмотрим прямоугольные треугольники ΔOAdT и ΔOBdT, вершины которых лежат на окружности пересечения и применяем теорему синусов. Тогда
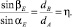
Теперь рассмотрим треугольники ΔACT и ΔBCT, которых получаем от базисного треугольника делением медианой TC, т.е. AC = BC, и аналогично применяя теорему синусов получаем
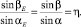
Для базисного треугольника ΔATB имеем
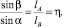
Из прямоугольных треугольников ΔAAhB и ΔABhB с общей гипотенузой AB (хорда) получаем
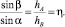
Таким образом, если имеем две точки A и B эллипса с радиусами кривизны ρA и ρB, то отношения между соответствующими элементами базисного треугольника ΔAEB, составленного из касательных LAτ, LBτ и хорды LAB, равны коэффициенту отношения радиусов кривизны η:
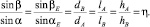(2)
Приведем пример, показывающий связь длин касательных с радиусами кривизны в точках касания. Пусть комбинированная беговая дорожка состоит из полудуг окружности x2 + y2 = 302 и полуэллипса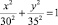 
. Выберем на эллиптической части стартовую точку – начальную точку сопряжения A(24; 21), где радиус кривизны ρA = 35,1253. Финишная точка – конечная точка сопряжения B на дуге окружности радиуса ρB = 30 определяется так, чтобы выполнялось условие (2): 
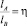. Искомая точка B(29,2997; 6,444). Имеем базисный треугольник с вершинами A(24; 21), B(29,2997; 6,444), B(32,3899; –7,9489). Тогда
,
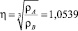lA = 15,5152, lB = 14,7209.
Действительно,
.
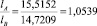Заключение
Полученные соотношения (2), характеризующие свойства эллиптической беговой дорожки, позволяет определить положение точки B и построить переходной участок, который обеспечивает безударный переход из одного участка в дру гой участок.
Библиографическая ссылка
Бостанов Б.О. УСЛОВИЯ ПЛАВНОГО СОПРЯЖЕНИЯ ПЕРЕХОДНОГО УЧАСТКА // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 2-2. – С. 164-167;URL: https://applied-research.ru/ru/article/view?id=8542 (дата обращения: 23.11.2024).