В настоящее время существует много различных решений задач консолидации земляных масс, полученные методами линейной механики уплотняемых сред, Однако они дают возможность оценить напряженно-деформированное состояние уплотняемого массива грунта только для небольших диапазонов напряжений. В действительности же, форма и размеры оснований сооружений при определенных нагрузках существенно изменяются, и принцип малости перемещений становится неприемлемым, т.е. линейный закон между напряжениями и деформациями уплотняемых сред перестает соблюдаться и он заменяется нелинейной зависимостью.
Замена линейного закона нелинейными зависимостями между напряжениями и деформациями составляет сущность физической нелинейности. Решением таких вопросов впервые занимался еще В.А. Флорин [6], один из основоположников механики грунтов. Он в своих работах, пользуясь уравнениями нелинейной теории ползучести, предложенной Н.Х. Арутюняном [1] дает основное уравнение одномерной консолидации, описывающее процесс уплотнения земляной среды с учетом старения и ползучести грунта. Получил решение для частного случая, когда уплотнение слоя грунта происходит под действием равномерно распределенной нагрузки.
Продолжая эту идею, в данной работе исследован процесс уплотнения упругоползучих земляных масс в двумерной постановке. При этом выведено уравнение уплотнения многофазных грунтов. Здесь зависимость между коэффициентом пористости и суммой главных напряжений принята в виде
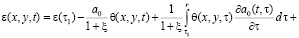
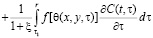, (1)
где
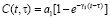; (2)
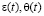– эти функции также изменяются по координатам x,y; 
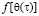– функция, характеризующая нелинейную зависимость между коэффициентом пористости 
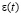и суммой главных напряжений 
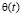в скелете грунта; 
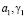– параметры ползучести; t1 – момент приложения внешней нагрузки; x – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта; 
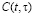– мера ползучести.
Причем выражение (1) является нелинейным и оно составлено на основе нелинейной теории ползучести. В этом уравнении фигурирует величина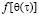 
, являющаяся нелинейной функцией напряжения. Для выражения 
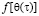обычно принимают степенную зависимость. Наиболее общая степенная функция 
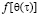может иметь вид
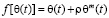. (3)
Выражение (3) используем далее при составлении окончательного выражения, определяющего вид основного уравнения рассматриваемого вопроса.
Уравнение уплотнения без учета ползучести относительно напряжений, согласно [6], имеет вид:
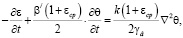(4)
где
;
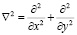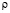– малый параметр; 
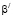– коэффициент объемного сжатия; 
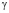– объемный вес воды; 
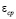– средний коэффициент пористости; k – коэффициент фильтрации.
Выражения (1), (2) и (3) подставив в (4), находим
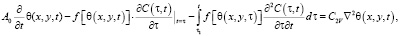(5)
где
;
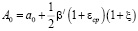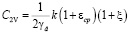. (6)
Полученное уравнение (5) при (6) дает возможность определить сумму главных напряжений в уплотняемом грунте, который обладает нелинейной ползучестью. Однако для определения искомой функции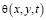 
, кроме граничных условий необходимо быть задано начальное условие. Оно имеет вид:
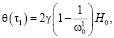(7)
где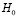 
– напорная функция для начального момента времени.
Таким образом, исследуемая задача сводится к решению уравнения (5), решение которого удовлетворяет начальному (7) и заданным граничным условиям.
В инженерной практике большой интерес представляет задача уплотнения земляной среды конечной мощности. В связи с этим рассмотрим уплотнение двухфазной среды с водоупором на глубине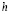 
ограниченной с боков водонепроницаемыми стенками, и находящейся под равномерно распределенной нагрузкой q на участке (–а, а), приложенной в момент времени 
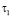. Граничными условиями этой задачи относительно суммы главных напряжений будут:
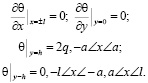(8)
Следовательно, требуется определить решение уравнения (5), удовлетворяющие граничным (8) и начальному (7) условиям.
Ввиду наличия малого параметра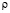 
в основном нелинейном уравнений (5), решение его представим в виде бесконечного ряда, т.е.
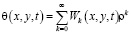, (9)
где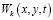 
– некоторая непрерывная функция, подлежащая определению.
Подставляя (9) и (2) в (5) и приравнивая коэффициентов при одинаковых степенях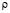 
, получим следующую систему реккурентных интегро-дифференциальных уравнений:
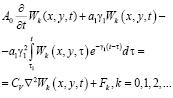(10)
; 
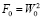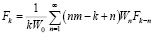
при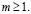 
Решив систему интегро-дифференциальных уравнений (10) находим все неизвестные функций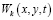 
. Их, подставив в (9) определим сумму главных напряжении. Причем функция 
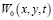вычисляется по формуле
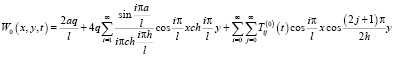, (11)
где функции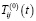 
имеют вид:
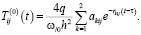(12)
Здесь
.
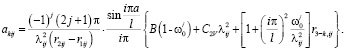
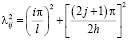Функция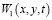 
, удовлетворяющая граничным и начальному условиям задачи имеет вид:
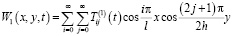, (13)
где
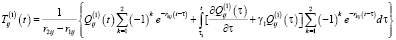. (14)
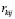– корни характеристического уравнения вида
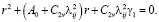
Функция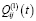 
в (14) определяется из следующего выражения
.
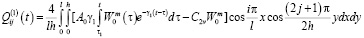Аналогичным методом можно будет решить и другие краевые задачи. В частности, функция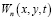 
имеет следующий вид:
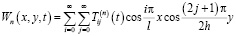, (15)
где
;
.
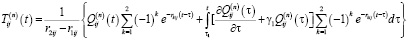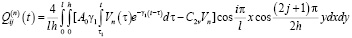После определения всех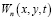 
сумму главных напряжений, согласно (9) и (11)-(15) вычисляем по формуле
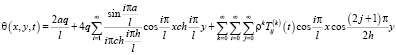. (16)
Тогда изменения порового давления во времени и пространственных координат имеет вид
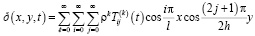. (17)
Вертикальные перемещения верхней поверхности уплотняемого массива или так называемое осадок слоя грунта при нелинейной его ползучести можно будет определить из следующего выражения:
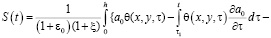
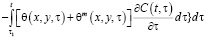. (18)
Используя соотношения (11)–(15) и (18) находим осадку уплотняемого массива
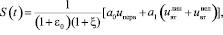(19)
где
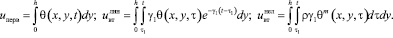
Таким образом, зная соотношения (12), (17) и (19) имеем возможность вычислить сумму главных напряжений, изменение порового давления и осадок уплотняемого слоя грунта для любого момента времени в каждой его точке.
Следует заметить, если в выражении (3) принять малый параметр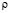 
=0, то получим 
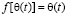. Это выражение соответствует линейной зависимости между напряжениями и деформациями ползучести. С другой стороны, деформации ползучести грунта являются линейными функциями напряжений только в том случае, если напряжения составляет достаточно малую часть предела прочности грунта. Если напряжения в грунте превосходит эту величину, появляется нелинейная зависимость. Для практического использования можно принять 
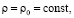тогда имеет место стационарная нелинейная ползучесть.
Следует заметить, что подобные задачи в другой постановке исследованы в [2-3].
Библиографическая ссылка
Дасибеков А., Юнусов А.А., Айменов Ж.Т., Юнусова А.А., Такибаева Г.А. НЕЛИНЕЙНЫЕ ЗАДАЧИ УПЛОТНЕНИЯ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 1-4. – С. 476-480;URL: https://applied-research.ru/ru/article/view?id=8583 (дата обращения: 24.04.2024).