В условиях катастрофического падения цен на нефть и существенного сокращения расходов, на первый план выдвинулась задача компенсации указанных потерь за счет реализации инвестиционных проектов. Проблема оценки эффективности проектов становится главной и повседневной задачей. В последнее время расширяется практика разработки динамических методов и моделей оценки проектов в реальном секторе экономики. Она преследует цель заинтересовать потенциальных участников проекта, показать, что участие в проекте будет ему выгодно. Поэтому основой проектного анализа является оценка эффективности инвестиционного проекта и выбор, при наличии альтернатив, лучшей из них. При этом оценка эффективности при значительных затратах даже в детерминированном случае не может использовать традиционные методы с использованием NPV.
Мы сконцентрируем внимание на подходах, связанных с работами [1, 2, 3 и 4], поскольку придерживаемся мнения, что с позиции сегодняшнего дня они наиболее интересны и гармонично вписываются в наши рассуждения.
Перечень символов
В модели используются следующие обозначения:
Ct – избыток или недостаток финансовых средств в момент времени t;
ft – элементы вектора структуры доходов для момента времени t;
j – индекс для j-го типа инвестиции (j=1,..,J);
k – индекс для k-го типа финансирования (k=1, ..., K);
Mt – элемент ряда базовых выплат для момента времени t;
t – индекс времени (t=0, ..., T);
T – горизонт планирования;
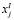– число инвестиционных проектов типа j;
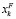– число проектов финансирования типа k;
Y – уровень доходов;
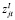– платеж, связанный с j-й инвестицией в момент времени t;
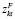– платеж, связанный с k-м финансированием в момент времени t.
Полный финансовый план
Для того чтобы инвестор в действительности мог принимать рациональные решения, проекты, которые он сравнивает друг другом, должны быть по-настоящему исключающими друг друга альтернативами. Поэтому мы должны суметь составить для каждой рассматриваемой программы инвестиции и финансирования полный финансовый план.
Модель для случая максимизации остаточной стоимости
Покажем, как можно использовать инструментарий линейного программирования для решения задачи одновременного инвестиционного и финансового планирования.
Целевая функция. Можно увидеть, что остаточная стоимость инвестора CT образуется как остаток после учёта всех платежей по инвестиционным проектам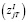 
, проектов финансирования 
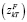, базового платежа (MT) и изъятия 
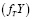в рамках горизонта планирования, а значит,
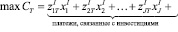
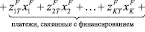
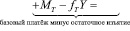
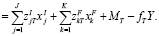
Необходимо максимизировать это выражение. Но в качестве целевой функции при линейном программировании можно также использовать вспомогательную величину
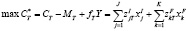(1)
поскольку окончательное изъятие инвестора и базовые платежи являются константами.
Дополнительные ограничения. Нам необходимо два вида дополнительных ограничений. С одной стороны, мы должны обеспечить, чтобы инвестор ни в одном из моментов своего планового периода не стал бы неплатёжеспособным (условия ликвидности), с другой – мы должны позаботиться о том, чтобы задаваемые количества проектов равнялись разумным, с точки зрения инвестора, величинам или же определялись ими (условия количества проектов).
Условия ликвидности. Ликвидность инвестора сохраняется, если сумма его выплат ни в один из моментов времени не превышает сумму его поступлений и/или финансовых запасов. Нам необходимы разные виды этих условий, а именно для момента времени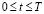 
, с одной стороны, и для момента времени 
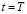– с другой. Между прочим, ограничение ликвидности можно очень легко вывести из схемы полного финансового плана.
Для всех моментов времени перед окончанием планового периода, очевидно, должно быть верно
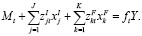
Если мы прибавим константу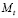 
к правой части этого уравнения, то условия ликвидности для момента времени 
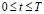выглядят следующим образом:
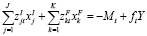. (2)
Наконец, мы обратимся к последнему столбцу таблицы полного финансового плана (т.е. табл. 4.16). Здесь, очевидно, верно
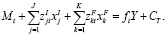
Если мы трактуем инвестора ликвидным лишь тогда, когда он достигает остаточного имущества, которое не меньше нуля, то условие ликвидности для момента времени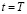 
выглядит следующим образом:
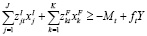. (3)
Теперь все условия ликвидности инвестора сформулированы.
Дополнительные условия количества проектов. Разумно полагать, что переменные решения не должны быть отрицательными, так как мы не можем реализовывать отрицательное число проектов. С другой стороны, количество проектов не должно превышать верхней границы, которую также устанавливает инвестор. Поэтому условия количества для инвестиций формулируются в виде
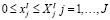(4)
и для финансирования
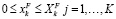. (5)
Теперь мы описали все необходимые дополнительные ограничения проблемы принятия решения. Если для этой проблемы нам удастся составить описывавшуюся до сих пор лишь с помощью символов систему уравнений (неравенств) с конкретными цифрами, то мы сможем также найти оптимальное решение. Определение этого решения происходит с помощью подходящих для линейного программирования правил расчёта, например с помощью алгоритма симплекс-метода.
Эндогенные расчетные ставки процента как «побочные продукты» линейного программирования
При решении на основе линейного программирования посредством симплекс-метода всегда образуются так называемые двойственные оценки. Они возникают в рамках дополнительных ограничений каждой линейной модели и показывают, на какую сумму увеличилось бы значение целевой функции, если бы мы увеличили правую часть дополнительных условий на одну единицу. С экономической точки зрения мы имеем здесь дело с предельной прибылью. В моделях одновременного инвестиционного и финансового планирования, которые были представлены нами, существует два вида дополнительных ограничений: условие ликвидности и условия количества проектов. Особый интерес для следующих рассуждений имеют двойственные оценки условий ликвидности.
Двойственная оценка условия ликвидности t-го периода (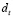
) показывает, на какую сумму увеличилось бы значение целевой функции (остаточное имущество, уровень дохода), если бы в этом периоде у инвестора имелось на одну денежную единицу больше.
Для применения метода чистой сегодняшней стоимости в случае многопериодного одновременного инвестиционного и финансового планирования отметим следующие рассуждения. Все проекты, которые содержатся в оптимальной программе, дают положительную предельную выгоду, в то время как проекты, от которых нужно отказаться, имеют отрицательную предельную выгоду. Под предельной выгодой при этом понимается относительное изменение остаточной стоимости или уровня дохода, которое можно ожидать при включении (только одной единицы) проекта в программу. Отсюда следует, что двойственные оценки dt больше предельной выгоды всех не содержащихся в оптимальной программе проектов, и что они одновременно меньше или равны предельным выгодам всех включенных в программу проектов.
На основе теоремы двойственности линейного программирования можно доказать, что относительные двойственные оценки
можно интерпретировать в качестве обоснованных множителей дисконтирования для выплат по всем проектам, конкурирующим за их включение в программу, так как если мы используем относительные двойственные оценки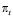 
в качестве множителей дисконтирования, то тогда все не относящиеся к оптимальной программе проекты имеют неотрицательную чистую сегодняшнюю стоимость, а этот же показатель всех проектов, от которых необходимо отказаться, является отрицательным.
Тогда чистая сегодняшняя стоимость рассчитывается по формуле:
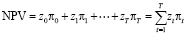(6)
Уравнение (6) можно записать и по-другому. Для этого мы определяем
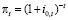
и выражаем через итоговую ставку процента. Это дает
,
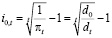и мы можем записать уравнение чистой сегодняшней стоимости в виде:
.
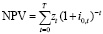Результаты ясно показывают, что все проекты, которые не принадлежат оптимальной программе, имеют отрицательную чистую сегодняшнюю стоимость. Значит, мы могли бы – точно так же, как и в случае одного периода, – принять оптимальные решения и с помощью (более простого по расчету линейного программирования) метода чистой сегодняшней стоимости, если бы нам только были известны эндогенные расчетные ставки процента. К сожалению, точные значения эндогенных расчетных ставок мы узнаем лишь после решения проблемы с помощью симплекс-метода, а значит тогда, когда у нас уже есть сведения об оптимальном решении.
Дальнейшее развитие данного подхода приводит к показателю, который можно трактовать как приведенный или (present equivalent income, PEI) проекта. Отметим важные особенности показателя PEI. Прежде всего, при исчислении этого показателя дисконтируются не только “обычные” денежные потоки проекта, но и дополнительные эффекты, порождаемые создаваемыми по проекту основными средствами. В традиционных расчетах эффективности это не учитывается, поскольку в них неявно предполагается, что любая фирма может получить любой кредит в любой момент времени. Если бы ограничения на кредит отсутствовали, то PEI совпало с NPV, т.к. ценность прав заимствования равнялась бы нулю. Кроме того, показатель PEI отражает такую денежную сумму, получение которой в начале расчетного периода эквивалентно (с точки зрения влияния на целевую функцию фирмы) всем затратам и результатам, связанным с участием фирмы в проекте. Изложенные соображения позволяют дать следующие определения этого показателя и входящей в его расчет ставки дисконта.
Текущий эквивалентный доход (обобщенный NPV, PEI) проекта – это текущий эквивалент денежных результатов проекта, т.е. такая сумма, получение которой в начальный момент эквивалентно для фирмы всей совокупности создаваемых по проекту основных средств и всех денежных поступлений и расходов, связанных с участием в проекте.
PEI проекта – сумма дисконтированных эквивалентных доходов проекта за весь период его реализации.
Ставка дисконта – темп падения оценок денег в оптимальном плане управления финансовой деятельностью фирмы.
Малым следует считать такой проект, реализация которого не меняет решение двойственной задачи, т.е. оценки активов и прав на образование задолженности.
Можно показать, что оценка эффективности проекта с помощью показателей типа NPV или PEI всегда будет завышена. Поэтому в тех случаях, когда проект имеет отрицательный PEI, он заведомо будет неэффективен, однако он может быть неэффективен и тогда, когда PEI положителен. Разумеется, последняя ситуация будет иметь место только для «достаточно крупных» проектов. Это может считаться некоторым оправданием для осторожного поведения некоторых инвесторов, отказывающихся участвовать в крупных проектах с положительным NPV.
Выводы. Развитие представленного подхода приводит к показателю, который можно трактовать как приведенный или текущий эквивалентный доход (present equivalent income, PEI) проекта. В работе отмечены важные особенности показателя PEI. Прежде всего, при исчислении этого показателя дисконтируются не только «обычные» денежные потоки проекта, но и дополнительные эффекты, порождаемые создаваемыми по проекту основными средствами. В традиционных расчетах эффективности это не учитывается, поскольку в них неявно предполагается, что любая фирма может получить любой кредит в любой момент времени.
Библиографическая ссылка
Грибов А.Ф. ДИНАМИЧЕСКИЕ МЕТОДЫ ОБОСНОВАНИЯ РЕШЕНИЙ ПО ВЫБОРУ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 1-4. – С. 570-573;URL: https://applied-research.ru/ru/article/view?id=8606 (дата обращения: 23.11.2024).