Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Абдула Ж. 1 Актаев Е.К. 1 Нурлыбаева А. 1 Аяпбергенова А.Е. 1

---

1 Таразский инновационно-гуманитарный университет

Для решения ограничения вредных выбросов необходимы разработки математической модели распространения примеси от источника загрязнения, учитывающая факторы на процесс.

Статья в формате PDF

1417 KB

метод расщепления

процесс распространения примеси

конвекция

диффузия

1. Айдосов А. Теоретические основы прогнозирования природных процессов и экологической обстановки окружающей среды. – Алматы, 2000 – С. 289.

2. Марчук Г.И. Математическое моделирование в проблеме окружающей среды. – М.: Наука, 1982.

Реальный процесс протекает при переменных профилях скорости. Поэтому интересна попытка создания математической модели распространения примеси при переменном профиле скорости. В такой постановке задача значительно усложняется, так как, возникает проблема по какому закону происходит изменение скорости, и в связи с этим усложняется форма самого устойчивого вычислительного алгоритма решения задачи, появляются также трудности в непосредственном реализации алгоритма на ЭВМ. В данной работе исследуется процесс распространения примеси точечного источника. На границах области и плоскости XY значения примеси принимаются равными нулю. Математическая модель задачи включает в себе уравнения переноса с источниковым членом. Рассмотрим дифференциальное уравнение в частных производных:

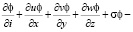
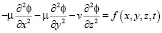(1)

При начальных м граничных условиях:

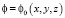при t = 0;

? = 0 в 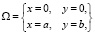(2)

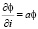при z = 0 и ? = 0 при Z = H (3)

где ? – интенсивность примеси;

u, v, w – составляющие вектора скорости вдоль оси OX, OY, OZ; μ > 0, v > 0 – горизонтальный и вертикальный коэффициенты вязкости;

σ = const > 0 – коэффициент взаимодействия субстанции;

a > 0 – коэффициент взаимодействия примеси с подстилающей поверхностью;

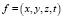– функция, характеризующая источник примеси, вида:

,

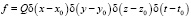где x0, y0, z0 – координаты источника;

t0 – время включения источника;

Q – его мощность.

Решение ищется в области ?x?, где

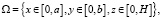
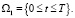
Переменное поле скорости накладывает определенные особенности в решении поставленной задачи. Возникает проблема при аппроксимации исходной дифференциальной задачи (1)-(3) соответствующими разностными задачами. Рассмотрим аппроксимации соответствующих операторов в (1) в случае переменности профиля скорости. Вначале рассмотрим уравнение переноса содержащее только конвективные члены, т.е. задача двумерная. Запишем исходное уравнение в форме [1]:

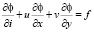в ?x?, (4)

где

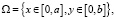
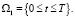
Компоненты скорости в общем случае являются функциями от х, у и z. В этом случае должно выполняться уравнение неразрывности:

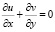
в каждый момент времени t.

Запишем (4) в ви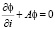де

где .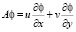

Введем скалярное произведение обычным образом, т.е.

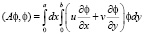(5)

Тогда с учетом уравнения неразрывности (5) можно преобразовать:

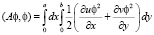(6)

Предположим, что А = А1 + А2. Тогда для каждого Аа (а = 1,2) имеем:

;

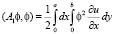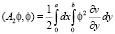. (7)

Рассмотрим теперь реальную трехмерную задачу, описываемую уравнением типа (1), но записанную в операторной форме:

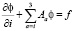в ?x? (8)

где введены следующие обозначения:

;

;

.

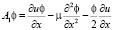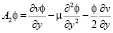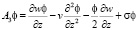Решение уравнения (8) ищется в области

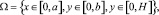
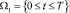
при следующих начальном и граничных условиях:

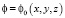при t = 0;

? = 0 при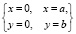

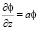при z = 0 ? = 0 при z = H. (9)

Для численного решения задачи будем использовать разностные схемы, основанные на методах расщепления [2]. Известны различные подходы и способы расщепления [2], например, по физическим процессам, по пространственным переменным. Нами использован метод расщепления, первый этап которого включает в себе горизонтальный перенос и диффузию примеси, а второй этап – конвекцию и диффузию в направлении оси ОZ. Однако, необходимо убедиться в применимости метода расщепления, т.е. следует проверить знакоопределенности Аа исходный дифференциальной задачи, для чего проверяем выполняемость соотношений: 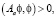а = 1, 2, 3. При рассмотрении случая u = u(z), v = const и w = const, согласно граничным условиям (9), а также из условий u = (z), v = const и w = const получим положительную определенность оператора А1. Аналогично можно показать положительную определенность оператора А2. Скалярное произведение (А3φ,φ), положительно – определенность имеет место при условии .

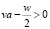Нами решена задача распространения монодисперсной пассивной примеси от мгновенного точечного источника в атмосфере в предположении частичного поглощения примеси поверхностью. Математическая модель описана уравнениями (8)-(9). Продольная составляющая скорости u – функция координаты z. Согласно изложенного выше алгоритма, основанного на методе расщепления, составлена программа счисленного счета. Получены распределения примеси для различных режимных параметров. Изменились виды начального профиля продольной скорости u = f(z), значения числа Рейнольдса. Проведены расчеты при наличии в области двух мгновенных источников. Решение задачи распределения пассивной монодисперсной примеси проведено численными методами. Полученные результаты согласуются с физическими закономерностями рассматриваемого течения.

Библиографическая ссылка