На сегодняшний день научное программирование претерпевает серьезные изменения: развивается множество интегрированных сред, основанных на алгоритмических языках, увеличивается число применений математических систем, которые имеют дружественный интерфейс и реализуют как стандартные, так и специальные операции, а также имеют мощные графические средства. Одной из таких систем является система Maple, которая содержит средства для выполнения быстрых численных расчетов, лежащих в основе математического моделирования различных процессов и явлений в физике, механике, экономике.
Одной из задач математического моделирования является разработка методов нахождения аналитических решений. Однако получение точных решений задач нелинейной теории упругости является одной из сложнейших проблем. В силу этого разработаны различные приближенные модели, позволяющие свести решение нелинейной задачи к решению ряда линейных задач. Одним из таких методов является метод конечных элементов. Однако в силу ограниченности ресурсов компьютеров, невозможно увеличивать число конечных элементов в зонах больших градиентов рассчитываемых полей. Поэтому данный подход плохо приспособлен к исследованию концентрации напряжений в зонах с большими градиентами напряжений, например, в окрестностях угловых точек отверстий. В связи с этим возникает задача разработки такого метода, который позволит свести решение нелинейных задач теории упругости к решению линейных задач и получить их аналитические решения. Данный аспект является важным, поскольку аналитические решения делают возможным анализ и оптимизацию влияния силовых и геометрических параметров на поведение решения.
Задача построения такой приближенной математической модели может быть осуществлена методом возмущений, предложенным в работе [9], который использует разложение в степенные ряды объектов, описывающих напряженно-деформированное состояние. Если удерживать один, два или три члена данного разложения, то будем получать решение в рамках эффектов первого, второго или третьего порядка. Для нахождения каждого члена разложения получается задача линейной теории упругости однородных тел, но с добавочными «внешними» поверхностными и объемными усилиями, зависящими от решений в рамках эффектов предыдущих порядков. Однако получаемые выражения достаточно громоздки, поэтому разложения выше второго порядка (эффектов второго порядка) редко используются. Появление современных пакетов символьной математики позволяет написать библиотеки программ, облегчающие действия с громоздкими выражениями, описывающими эффекты первого, второго или третьего порядков при произвольном напряженно-деформированном состоянии.
Применение пакета символьных вычислений Maple в задачах нелинейной теории упругости
В механике сплошных сред использование систем аналитических вычислений началось с самых первых дней появления ЭВМ с помощью программ, разработанных самими механиками. Разнообразие задач и существование аналитических методов построения их решений способствовали широкому применению разнообразных систем аналитических вычислений. На базе пакета символьной математики Maple для нахождения аналитического решения задач о концентрации напряжений около отверстий создан комплекс программ, который позволяет выполнять все символьные вычисления в автоматическом режиме. Все выполняемые операции распространены на тензоры до второго порядка включительно, компоненты которых являются рядами по малому параметру. Над этими тензорами, имеющими тип Array, получены процедуры для инвариантных дифференциальных операторов и процедуры выделения коэффициентов в этих разложениях по малому параметру, которые являются тензорами нулевого или первого ранга. Данный алгоритм позволяет в рамках эффектов второго порядка находить выражение коэффициента концентрации напряжений для различных форм отверстия при различных видах деформации.
Созданная специализированная система вычислений отличается тем, что библиотека программ не использует формулы, полученные в [1, 2], а вычисляет разложения всех объектов, описывающих напряженно-деформированное состояние, начиная с разложения вектора перемещения. Все алгебраические операции над рядами в предположении их абсолютной сходимости выполняются в Maple пакетом powseries. Этим рядам достаточно придать вид разложения по малому параметру и зафиксировать порядок представления результата относительно данного параметра. Так моделируются эффекты соответствующего порядка. Для работы с дифференциальными уравнениями в частных производных используется пакет PDEtools. Граничные задачи линейной теории упругости для эффектов первого и второго порядков сводятся к интегральным уравнениям теории функций комплексной переменной [3]. В тех случаях, когда область отверстия имеет произвольную форму, необходимо рассмотреть комплексное представление перемещений и напряжений для эффектов первого и второго порядка. Для этого необходимо ввести в рассмотрение функцию z = υ(ξ), которая осуществляет конформное отображение внешности замкнутого контура на внешность окружности единичного радиуса 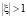 . Потребуем, чтобы точке ξ = ∞ соответствовала точка z = ∞. В качестве областей, характеризующих форму отверстия, рассматриваются только те, которые можно конформно отобразить на внешность окружности единичного радиуса с центром в начале координат с помощью функции вида
. Потребуем, чтобы точке ξ = ∞ соответствовала точка z = ∞. В качестве областей, характеризующих форму отверстия, рассматриваются только те, которые можно конформно отобразить на внешность окружности единичного радиуса с центром в начале координат с помощью функции вида
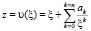 ,
,
где 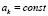 .
.
В работах [5–8] исследовано влияние внешней нагрузки на величину коэффициента концентрации напряжений в случае равномерного и одноосного растяжения пространства на бесконечности с эллиптической, треугольной и квадратной полостями. Для каждой из этих областей интегральные уравнения теории функций комплексного переменного приводятся к алгебраическим уравнениям с помощью интегралов типа Коши. Для эффектов первого и второго порядков искомые потенциалы аппроксимируются разложением в ряды Лорана, а коэффициенты находятся из условия удовлетворения граничным условиям на бесконечности и на контуре отверстия. При этом часть неизвестных коэффициентов находится из решения алгебраической системы линейных уравнений, полученной с помощью предельного перехода на бесконечности. Для нахождения остальных коэффициентов необходимо вычислить интегралы типа Коши на контуре отверстия.
Точное вычисление интеграла типа Коши в разложении по малому параметру до второго порядка
Для эффектов второго порядка в интегральных уравнениях присутствует слагаемое вида
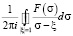 ,
,
которое зависит от решения, проведенного в рамках эффектов первого порядка. Подынтегральная плотность F(σ) в зависимости от типа отверстия и граничных условий может быть весьма сложной. В пакете Maple нет специальных процедур и функций для точного вычисления интеграла типа Коши. Тем не менее, пользуясь основными свойствами интеграла типа Коши [3], можно реализовать алгоритм его точного вычисления. В пакете Maple присутствуют возможности разложения функции в ряд в окрестности особой точки и асимптотических разложений в окрестности бесконечно удаленной точки. Этого достаточно для вычисления интегралов типа Коши на окружности единичного радиуса. Подынтегральная плотность является дробно-рациональной функцией и имеет особенности типа полюсов в бесконечно удаленной точке и в конечном наборе конечных точек 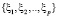 вне окружности единичного радиуса, являющихся корнями знаменателя. Средствами пакета Maple можно получить главные части разложений в ряды функции подынтегральной плотности F(ξ) в окрестностях этих точек в виде:
вне окружности единичного радиуса, являющихся корнями знаменателя. Средствами пакета Maple можно получить главные части разложений в ряды функции подынтегральной плотности F(ξ) в окрестностях этих точек в виде:
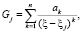
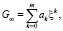
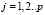 .
.
Тогда по [3] получаем
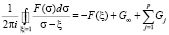
при интегрировании против хода часовой стрелки.
В качестве примера вычисления рассмотрим интеграл с плотностью вида
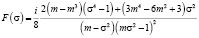 ,
,
где m – коэффициент формы. Интеграл с поверхностной плотностью данного вида встречается в эффектах второго порядка в задаче о равномерном растяжении на бесконечности пространства с эллиптической полостью [1, 2]. При 0 < m < 1 получаем эллипс с центром в начале координат и полуосями a = 1 + m, b = 1 – m. При m = 0 имеем окружность единичного радиуса, а при m = 1 – симметричный разрез вдоль оси OX длины 2.
Асимптотическое разложение подынтегральной плотности F(σ) в окрестности бесконечно удаленной точки принимает вид
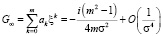 .
.
Далее находим, что вне окружности единичного радиуса функция подынтегральной плотности F(σ) имеет два полюса: 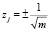 , j = 1, 2. В окрестностях данных полюсов разложение в ряд Лорана подынтегральной плотности F(σ) соответствует разложениям
, j = 1, 2. В окрестностях данных полюсов разложение в ряд Лорана подынтегральной плотности F(σ) соответствует разложениям
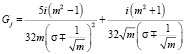 ,
,
j = 1, 2.
Таким образом, точное значение интеграла типа Коши на окружности единичного радиуса имеет следующий вид:
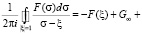
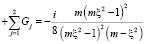 .
.
Приближенное вычисление интеграла типа Коши в разложении по малому параметру до второго порядка
Ключевым моментом, от которого зависит успех вычисления интеграла типа Коши, является возможность точного нахождения корней знаменателя. В тех случаях, когда аналитически найти точное значение корней знаменателя поверхностной плотности F(σ) система Maple не может, приходится проводить вычисления интеграла типа Коши приближенными методами.
Проблемам приближенного вычисления интегралов типа Коши посвящена довольно обширная литература. Это связано с тем, что в настоящее время теория сингулярных интегралов и сингулярных интегральных уравнений с ядром Коши находит широкое приложение в математических и технических исследованиях. В созданной библиотеке программ на базе пакета символьной математики Maple для приближенного вычисления интеграла типа Коши применяется следующая квадратурная формула [4]:
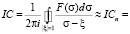
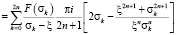 .
.
Здесь 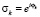 ,
, 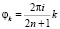 . Если
. Если 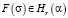 , то
, то 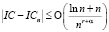 .
.
В качестве примера проведем сравнение точного и приближенного выражений интеграла типа Коши из предыдущего примера. Функция подынтегральной плотности при m = 0,8 равна
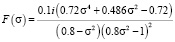 ,
,
а точное выражение интеграла типа Коши на окружности единичного радиуса принимает вид
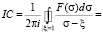
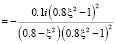 .
.
Выражение приближенного значения интеграла типа Коши достаточно громоздко при n > 10. Для визуализации сравнения полученных выражений будем строить годографы векторов, компонентами которых являются значения вещественной и мнимой частей интеграла типа Коши на окружности единичного радиуса. Применение процедуры приближенного вычисления интеграла типа Коши продемонстрировано на рисунке.
Видим, что при увеличении числа итераций с 30 до 90 погрешность вычисления приближенного значения интеграла типа Коши на окружности единичного радиуса от его точного значения не превосходит 1 %. Поэтому в случае, когда функция поверхностной плотности F(σ) имеет полюсы, которые система Maple может вычислить только приближенно, точное вычисления интеграла типа Коши оказывается невозможным. Поэтому необходимо проводить расчеты, используя процедуры численного вычисления, которые тем точнее, чем выше число итераций в квадратурной формуле.
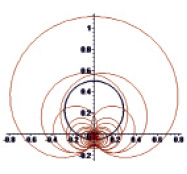
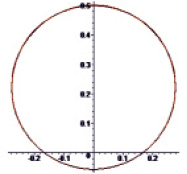
а) число итераций n = 30 б) число итераций n = 90
Годографы векторов, компонентами которых являются значения вещественной и мнимой частей интеграла типа Коши на окружности единичного радиуса. Тонкая линия соответствует приближенному решению в рамках эффектов второго порядка, толстая линия соответствует точному решению в рамках эффектов второго порядка
Выводы
Применение созданной библиотеки символьных блоков, реализованной в среде Maple, позволяет быстро и эффективно использовать метод эффектов второго порядка для нахождения аналитического решения задач о концентрации напряжений, визуализации и анализа полученного решения. Кроме того, алгоритм может быть применен как для выполнения арифметических, так и дифференциальных операций над тензорами, компоненты которых являются рядами.
Библиографическая ссылка
Щукина Н.А. ОСОБЕННОСТИ ВЫЧИСЛЕНИЙ ИНТЕГРАЛА ТИПА КОШИ В РАМКАХ ЭФФЕКТОВ ВТОРОГО ПОРЯДКА // Международный журнал прикладных и фундаментальных исследований. 2016. № 4-3. С. 540-544;URL: https://applied-research.ru/ru/article/view?id=9008 (дата обращения: 02.02.2026).

