Рассматривается гипотеза Лежандра, в справедливости которой убедиться довольно просто: достаточно, используя формулу Гаусса, вычислить значение π((n + 1)2) – π(n2).
«В гипотезе Лежандра идет речь о количестве простых чисел и их распределении. Точная формулировка гипотезы выглядит так: «для всякого натурального числа n между n2 и (n + 1)2 всегда найдется простое число». В действительности для каждого n, по-видимому, найдется больше одного простого числа» [1, с. 59].
Чтобы убедиться в справедливости этой гипотезы достаточно, используя формулу Гаусса: π(n) ≈ n/ln(n), обнаруженную им эмпирически и впоследствии доказанную Адамаром и Валле-Пуссеном [2, с. 58], вычислить разность между π((n + 1)2) и π(n2).
π((n+1)2) – π(n2) = 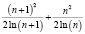 (*)
(*)
В таблице приведены следующие значения: I – n; II – π((n+1)2); III – π(n2); IV – значение выражения (*); V – действительное количество простых чисел между n2 и (n+1)2; VI – значение n/ln(n).
Таблица количества простых чисел
|
I |
II |
III |
IV |
V |
VI |
|
10 |
25 |
21 |
4 |
5 |
4 |
|
20 |
72 |
66 |
6 |
7 |
7 |
|
30 |
139 |
132 |
7 |
8 |
9 |
|
40 |
226 |
216 |
10 |
12 |
11 |
|
50 |
330 |
319 |
11 |
11 |
13 |
|
60 |
452 |
439 |
13 |
16 |
15 |
|
70 |
591 |
576 |
15 |
21 |
16 |
|
80 |
746 |
730 |
16 |
13 |
18 |
|
90 |
917 |
900 |
17 |
20 |
20 |
|
100 |
1 105 |
1 085 |
20 |
22 |
22 |
Как видно из таблицы, простых чисел между n2 и (n + 1)2 почти столько же, сколько и простых чисел, не превосходящих n.
Аналогичным образом можно убедиться в справедливости постулата Бертрана, уже доказанного П.Л. Чебышевым.
Библиографическая ссылка
Черкасов М.Ю. О СПРАВЕДЛИВОСТИ ГИПОТЕЗЫ ЛЕЖАНДРА // Международный журнал прикладных и фундаментальных исследований. 2016. № 4-3. С. 649-649;URL: https://applied-research.ru/ru/article/view?id=9045 (дата обращения: 02.02.2026).

