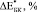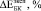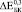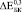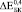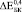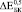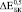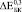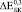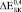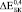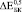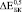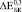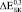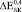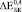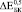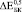В качестве материалов для имплантатов ортопедического профиля традиционно используют металлы и их сплавы. Наибольшее распространение получили чистый титан и его сплавы, т.к. наряду с превосходной биосовместимостью, они имеют высокое соотношение прочность-вес, низкий модуль упругости, менее подвержены усталостному разрушению [4]. Однако имплантаты ортопедического профиля из монолитных сплавов по механическим характеристикам не соответствуют окружающей костной ткани. Это несоответствие нарушает нормальное функционирование прилегающей ткани, что может вызвать ее резорбцию, инфицирование. Кроме того, для хорошей связи между костью и имплантатом его поверхность должна иметь вполне определенную геометрию. Поэтому открыто – ячеистые пористые металлы являются перспективным материалом для травматологии и ортопедии [5]. Их модуль упругости может приближаться к модулю упругости кости, а поверхность имеет открытые каналы для врастания костной ткани. Кроме того, такие материалы можно рассматривать как трехмерные скэффолды, которые могут быть носителями стимуляторов остеогенеза и антибиотиков.
При длительном контакте пористых металлов с костной тканью образуется биокомпозит, эффективные механические свойства которого зависят от свойств его компонент – пористой матрицы и костной ткани. При этом свойства костной ткани меняются со временем: чем дольше пористый металлический имплантат находится в контакте с костью реципиента, тем более зрелая костная ткань заполняет его поры [2]. Соответственно и механические свойства биокомпозита будут претерпевать изменения до тех пор, пока поры имплантата не будут заполнены наиболее твердой компактной костью. Однако, экспериментальное исследование прочностных характеристик биокомпозитов является сложным, дорогостоящим и длительным процессом. Поэтому развитие численных методов моделирования упругого поведения гетерогенных структур актуальной задачей.
Цель настоящей работы заключалась в численной оценке модуля Юнга биокомпозитов с использованием известных моделей и экспериментальных данных по кинетике изменения биологической компоненты. Рассмотрены биокомпозиты, в состав которых входит титан с объемной долей пор 0,3, 0,4 и 0,5 и костная ткань с модулем Юнга от 5 до 20 ГПа. Оценка применимости предложенной методики расчетов для прогнозирования свойств биокомпозитов сделана на основе сравнительного анализа расчетных и экспериментальных зависимостей модуля Юнга биокомпозитов от времени их формирования.
Материалы и методы исследования
Титановые имплантаты с пористостью 0,3, 0,4 и 0,5 (доля общего объема имплантата) получены методом прессования гранул титана губчатого с последующим вакуумным отжигом и нанесением на их поверхность пленки алмазоподобного углерода толщиной 30-50 нм. Открытые взаимосвязанные поры размером от нескольких до нескольких сотен микрон in vitro насыщались аутологичными клетками костного мозга [6-7, 9]. Клиновидные имплантаты внедряли в мыщелки большеберцовой и бедренной кости овец сроком на 8, 24 и 52 недели. Клиновидная форма имплантатов позволила избежать применения дополнительных пластин для их фиксации в костном дефекте. По истечении каждого срока имплантаты с вросшей костной тканью (биокомпозиты) вырезались из кости, и подвергались испытанию на сжатие на универсальной испытательной машине INSTRON. По диаграммам напряжение-деформация вычислялся модуль Юнга биокомпозита.
Расчет упругих характеристик биокомпозита проведен с использованием метода конечных элементов. Для описания напряженно-деформированного состояния биокомпозита использованы модули объемной деформации и сдвига, которые между собой однозначно функционально связаны [3].
Объемный модуль k, модуль сдвига μ, модуль Юнга E и коэффициент Пуассона ν в линейной теории упругости связаны между собой соотношениями:
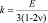 , (1)
, (1)
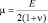 , (2)
, (2)
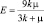 . (3)
. (3)
Ранее авторами был проведен расчет упругих характеристик биокомпозита пористый титан (пористость 0,4) – костная ткань с использованием полидисперсной модели составных частиц [1, 6], в которой гетерогенная структура рассматривается как непрерывная среда, образованная составными частицами различного размера (рис. 1, а). Для каждой составной частицы независимо от ее абсолютного размера отношение радиусов включения и внешней сферы принимается постоянным (a/b = const). Решение уравнения равновесия, при условиях непрерывности r = b 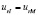
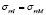 (где u – перемещение, s – напряжение, индекс I относится к включению, индекс М – матрице) вместе с граничными условиями r = b,
(где u – перемещение, s – напряжение, индекс I относится к включению, индекс М – матрице) вместе с граничными условиями r = b, 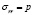 , позволяет найти эффективный объемный модуль k* (Ур.4) и эффективный модуль сдвига μ* (Ур.5) композита.
, позволяет найти эффективный объемный модуль k* (Ур.4) и эффективный модуль сдвига μ* (Ур.5) композита.
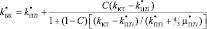 (4)
(4)
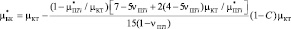 (5)
(5)
где С – объемная доля включений или пористость, индекс БК означает биокомпозит, ПTi – пористый титан, КТ – костная ткань.
Эта модель дает разумные результаты для реальных систем. Однако рассчитанные из Ур.5 модули сдвига композитов не совпадают с экспериментально измеренными, за исключением очень малых и очень больших долей включений. Кроме того, применение этой модели ограничено для композитов, в которых модули сдвига матрицы и включения имеют сильно отличающиеся модули сдвига [1]. Наши расчеты модуля Юнга биокомпозита, состоящего из пористого титана (С = 0,4) и костной ткани, модули сдвига которых отличаются в 4-5 раз, также показали некоторое расхождение с экспериментальными данными [6].
Для более точной оценки модуля сдвига необходим другой подход. Разумное приближение к решению этой проблемы найдено в трехфазной модели [6]. В трехфазной модели рассматривается одна составная сферическая частица, которая окружена эквивалентной гомогенной средой (рис. 1б).

Рис. 1. Полидисперсная модель (а) и трехфазная модель (б)
Включение образовано двумя фазами, поэтому в отличие от полидисперсной модели однородное деформированное состояние не реализуется. В трехфазной модели эффективные свойства композита определяются через равенство энергии, а именно, энергия деформирования составной частицы и эффективной гомогенной среды одинакова при равенстве осредненных деформаций. При этом эффективные объемные модули упругости k* для полидисперсной и трехфазной моделей идентичны. Модуль сдвига биокомпозита в трехфазной модели находится из Ур.(6):
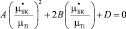 (6)
(6)
где коэффициенты А, В и D зависят от µTi, nTi, µКТ, nКТ и объемной доли включений С [1].
Эффективные модули пористого титана 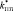 и
и 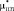 могут быть найдены из Ур. (4-5) при условии, что в его порах отсутствуют какие-либо включения. Из Ур. (3) можно найти эффективный модуль Юнга
могут быть найдены из Ур. (4-5) при условии, что в его порах отсутствуют какие-либо включения. Из Ур. (3) можно найти эффективный модуль Юнга 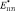 . Значения
. Значения 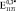 ,
, 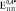 и
и 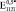 (где верхние индексы 0,3, 0,4 и 0,5 означают пористость) превысили экспериментально полученные
(где верхние индексы 0,3, 0,4 и 0,5 означают пористость) превысили экспериментально полученные 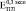 ,
, 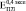 и
и 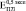 более чем на порядок. Анализ литературных данных показал, что независимо от способа получения пористого титана, значения
более чем на порядок. Анализ литературных данных показал, что независимо от способа получения пористого титана, значения 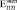 существенно ниже расчетных с использованием различных моделей [8]. Следовательно, для расчета эффективных характеристик биокомпозита на основе пористого металла необходимо вводить поправочные коэффициенты.
существенно ниже расчетных с использованием различных моделей [8]. Следовательно, для расчета эффективных характеристик биокомпозита на основе пористого металла необходимо вводить поправочные коэффициенты.
Поправочные коэффициенты l и g вычисляются из следующих соотношений: 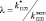 и
и 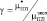 . Коэффициент Пуассона n определяется из соотношения:
. Коэффициент Пуассона n определяется из соотношения:
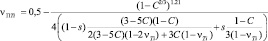 (6)
(6)
где С – пористость, 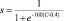 .
.
Расчетные значения λ, γ и n представлены в табл. 1.
Таблица 1
Поправочные коэффициенты для 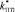 ,
, 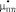 и коэффициент Пуассона
и коэффициент Пуассона
|
Пористость |
λ |
γ |
n |
|
0,3 |
0,062 |
0,119 |
0,30 |
|
0,4 |
0,054 |
0,107 |
0,23 |
|
0,5 |
0,011 |
0,021 |
0,16 |
Биологическая компонента, заполняя все поры, с течением времени претерпевает изменения [2]. Зависимость относительного предела прочности костной ткани от времени ее формирования (t) описывается полиномом второй степени [6]:
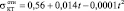 (7)
(7)
В биокомпозите костная ткань является включением. Кинетику изменения ее модуля Юнга можно представить как 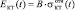 , где B – модуль Юнга кости. Решение системы Ур. (1-3) дает зависимости kКТ (t) и µКТ (t).
, где B – модуль Юнга кости. Решение системы Ур. (1-3) дает зависимости kКТ (t) и µКТ (t).
Временные зависимости эффективных модулей биокомпозита 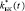 и µБК (t) в модели составных частиц рассчитываются из Ур. (4-5), в трехфазной – из Ур. (4, 6). Матрица в биокомпозите – пористый титан с эффективными модулями l
и µБК (t) в модели составных частиц рассчитываются из Ур. (4-5), в трехфазной – из Ур. (4, 6). Матрица в биокомпозите – пористый титан с эффективными модулями l 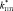 , g
, g 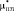 , включение – костная ткань с модулями kКТ (t), µКТ (t). Зависимость
, включение – костная ткань с модулями kКТ (t), µКТ (t). Зависимость 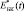 получают из Ур. (3).
получают из Ур. (3).
Результаты исследования и их обсуждение
Экспериментальные зависимости модуля Юнга биокомпозитов от времени их формирования представлены на рис. 2.
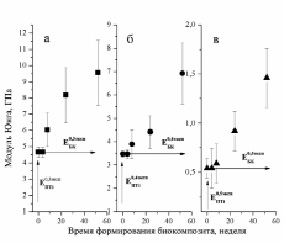
Рис. 2. Зависимости модуля Юнга биокомпозита от времени его формирования. а – биокомпозит на основе титана пористостью 0,3; б – пористостью 0,4; в – пористостью 0,5
Бикомпозиты формировались при остеоинтеграции пористого титана с объемной долей пор 0,3 (рис. 2, а), 0,4 (рис. 2, б) и 0,5 (рис. 2, в). Значения при t = 0 (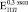 ,
, 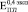 и
и 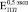 ) соответствуют модулю Юнга пористого титана, не содержащего включения. Через четыре недели формирования биокомпозита его модуль Юнга не отличаются от модуля Юнга исходного пористого титана. К восьми неделям происходит незначительное увеличение
) соответствуют модулю Юнга пористого титана, не содержащего включения. Через четыре недели формирования биокомпозита его модуль Юнга не отличаются от модуля Юнга исходного пористого титана. К восьми неделям происходит незначительное увеличение 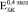 (рис. 2. б) и
(рис. 2. б) и 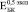 (рис. 2. в). В то же время
(рис. 2. в). В то же время 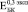 возрастает в ~ 1,5 раза по сравнению с
возрастает в ~ 1,5 раза по сравнению с 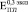 (рис. 2. а). Аналогичная тенденция наблюдается до 24 недель остеоинтеграции:
(рис. 2. а). Аналогичная тенденция наблюдается до 24 недель остеоинтеграции:
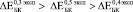 ,
,
где 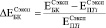 , С – пористость.
, С – пористость.
В интервале от 24 до 52 недель меньше всего прирастает 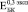 :
: 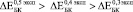 , т.е. наблюдается прямая зависимость изменения модуля Юнга от объема вросшей ткани.
, т.е. наблюдается прямая зависимость изменения модуля Юнга от объема вросшей ткани.
Изменение механических свойств биокомпозита при остеоинтеграции является следствием трансформации биологической компоненты, т.к. титановая матрица стационарна. Биологическая компонента – это образующаяся в имплантате костная ткань, прочность которой определяется, в основном, минеральной фазой, входящей в ее структуру [2]. Т.е. механические свойства биокомпозита должны определяться как качеством (зрелостью) новообразованной костной ткани, так и ее объемом. В численных расчетах упругих модулей биокомпозита качество костной ткани выражено через зависимость 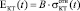 , где В изменяется в интервале от 5 до 20 ГПа, а ее объем – через пористость С в Ур. (4-6).
, где В изменяется в интервале от 5 до 20 ГПа, а ее объем – через пористость С в Ур. (4-6).
Экспериментальные (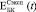 ) и расчетные (
) и расчетные (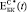 ) зависимости для биокомпозитов на основе пористого титана с С = 0,3, 0,4 и 0,5 показаны на рис. 3. Расчеты были выполнены с использованием модели I (полидисперсная модель MI) и модели II (трехфазная модель MII) при значениях модуля Юнга костной ткани: B = 5, 10, 15 и 20 ГПа. До 24 недель расчеты по модели I согласуются с экспериментальными данными при условии формирования костной ткани с модулем Юнга от 5 до 15 ГПа. При t > 24 наблюдается довольно большое отличие между расчетными и экспериментальными значениями (
) зависимости для биокомпозитов на основе пористого титана с С = 0,3, 0,4 и 0,5 показаны на рис. 3. Расчеты были выполнены с использованием модели I (полидисперсная модель MI) и модели II (трехфазная модель MII) при значениях модуля Юнга костной ткани: B = 5, 10, 15 и 20 ГПа. До 24 недель расчеты по модели I согласуются с экспериментальными данными при условии формирования костной ткани с модулем Юнга от 5 до 15 ГПа. При t > 24 наблюдается довольно большое отличие между расчетными и экспериментальными значениями (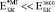 ) даже при формировании компактной костной ткани. Расчет модуля Юнга биокомпозитов по модели II дает более хорошую корреляцию расчетных и экспериментальных зависимостей.
) даже при формировании компактной костной ткани. Расчет модуля Юнга биокомпозитов по модели II дает более хорошую корреляцию расчетных и экспериментальных зависимостей.
Экспериментально измеренные значения 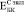 , где С – пористость, лежат в области, заключенной между расчетными кривыми
, где С – пористость, лежат в области, заключенной между расчетными кривыми 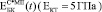 и
и 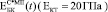 (рис. 3).
(рис. 3).
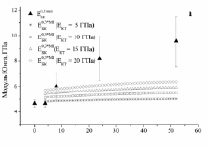
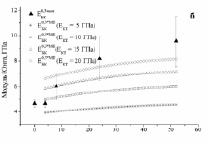
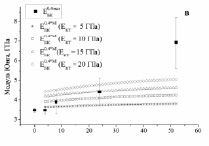
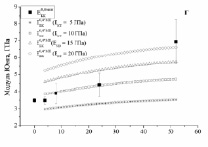


Рис. 3. Экспериментальные и расчетные зависимости модуля Юнга биокомпозита на основе титана пористостью 0,3 (а,б), 0,4 (в,г) и 0,5 (д,е). МI означает, что расчеты сделаны по модели I, МII – по модели II
При этом в интервале от 4 до 24 недель экспериментальные значения Модуля Юнга хорошо согласуются с расчетными при условии заполнения пор костной тканью, имеющей модуль Юнга от 5 до 15 ГПа, в интервале от 24 до 52 недель – при условии заполнения пор костной тканью, имеющей модуль Юнга от 10 до 20 ГПа.
До 24 недель формирования биокомпозита костная ткань, заполняющая поры, близка по составу к губчатой, т.е. 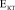 = (3–5) ГПа, что сравнимо с
= (3–5) ГПа, что сравнимо с 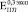 и
и 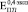 . После 24 недель костная ткань в порах по свойствам начинает приближаться к компактной с модулем Юнга до 20 ГПа, что в несколько раз превышает
. После 24 недель костная ткань в порах по свойствам начинает приближаться к компактной с модулем Юнга до 20 ГПа, что в несколько раз превышает 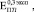
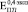 и
и 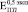 . При большом отличии модуля сдвига матрицы и включения расчеты по модели II лучше согласуются с экспериментом.
. При большом отличии модуля сдвига матрицы и включения расчеты по модели II лучше согласуются с экспериментом.
Расчетные (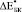 ) и экспериментальные (
) и экспериментальные (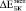 ) значения относительного изменения модуля Юнга биокомпозитов представлены в табл. 2.
) значения относительного изменения модуля Юнга биокомпозитов представлены в табл. 2. 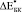 и
и 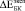 при t = 8 недель сопоставимы по величине при использовании обеих моделей. Однако для биокомпозита с С = 0,3
при t = 8 недель сопоставимы по величине при использовании обеих моделей. Однако для биокомпозита с С = 0,3 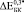 и
и 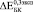 имеют близкие значения только при B = 15 ГПа (модель II) и B = 20 ГПа (модель I). Маловероятно, что к 8 неделям в порах имплантата образуется костная ткань близкая к компактной [2]. Можно предположить, что увеличение модуля Юнга на 28 % при С = 0,3 связано с заполнением каналов в структурообразующих губчатых гранулах. С одной стороны, при С = 0,3 мы имеем матрицу с максимальным содержанием титановой фракции, с другой стороны, эта матрица не имеет протяженных сквозных каналов как при С = 0,4 и 0,5. Вероятно, такая структура создает наиболее благоприятные условия для формирования кости не только в порах между гранулами, но и каналах, уходящих вглубь гранул. При t = 24 и 52 недели во всех случаях хороший результат получен при расчетах с использованием модели II.
имеют близкие значения только при B = 15 ГПа (модель II) и B = 20 ГПа (модель I). Маловероятно, что к 8 неделям в порах имплантата образуется костная ткань близкая к компактной [2]. Можно предположить, что увеличение модуля Юнга на 28 % при С = 0,3 связано с заполнением каналов в структурообразующих губчатых гранулах. С одной стороны, при С = 0,3 мы имеем матрицу с максимальным содержанием титановой фракции, с другой стороны, эта матрица не имеет протяженных сквозных каналов как при С = 0,4 и 0,5. Вероятно, такая структура создает наиболее благоприятные условия для формирования кости не только в порах между гранулами, но и каналах, уходящих вглубь гранул. При t = 24 и 52 недели во всех случаях хороший результат получен при расчетах с использованием модели II.
Таблица 2
Расчетные и экспериментальные изменения модуля Юнга биокомпозитов
|
Срок, неделя |
Модель |
|
|
||||
|
В, ГПа |
|||||||
|
5 |
10 |
15 |
20 |
||||
|
8 |
|
I |
3 |
10 |
17 |
23 |
28 |
|
|
II |
2 |
10 |
30 |
48 |
||
|
|
I |
9 |
28 |
37 |
46 |
12 |
|
|
|
II |
5 |
15 |
38 |
58 |
||
|
|
I |
7 |
18 |
28 |
38 |
9 |
|
|
|
II |
4 |
26 |
52 |
75 |
||
|
24 |
|
I |
5 |
13 |
22 |
29 |
74 |
|
|
II |
7 |
21 |
43 |
63 |
||
|
|
I |
12 |
34 |
45 |
57 |
27 |
|
|
|
II |
5 |
26 |
52 |
75 |
||
|
|
I |
10 |
23 |
35 |
47 |
70 |
|
|
52 |
|
II |
4 |
39 |
69 |
96 |
|
|
|
I |
7 |
17 |
26 |
35 |
104 |
|
|
|
II |
17 |
30 |
55 |
76 |
||
|
|
I |
10 |
23 |
37 |
48 |
99 |
|
|
|
II |
11 |
36 |
65 |
91 |
||
|
|
I |
12 |
27 |
42 |
56 |
170 |
|
|
|
II |
11 |
51 |
85 |
115 |
||
Таким образом, использование экспериментальных данных по свойствам отдельных составляющих композита (металлической матрицы и биологической компоненты) в модельных расчетах модуля Юнга, дает возможность прогнозировать кинетику изменения свойств биокомпозитов.
Заключение
Предложен алгоритм расчета зависимости модуля Юнга биокомпозита от времени его формирования (4 – 52 недели). В расчеты заложено использование упругих характеристик металлической матрицы и кинетики изменения прочностных свойств костной ткани. Расчеты проведены для композитов на базе пористого титана с объемной долей пор 0,3, 0,4 и 0,5 с использованием двух моделей (полидисперсной и трехфазной). Расчетные зависимости сопоставлены с экспериментальными. Показано, что расчетные значения модуля Юнга биокомпозитов коррелируют с экспериментально полученными величинами при варьировании модуля Юнга биологической компоненты от 5 до 20 ГПа. Это отражает реальный процесс остеоинтеграции пористых металлов, когда качество новообразованной костной ткани определяется временем контакта имплантата с материнским ложем. Подтверждено, что трехфазная модель более пригодна для композитов, фазовые составляющие которых сильно отличаются по упругим свойствам. Расчеты по этой модели могут быть использованы для прогнозирования свойств биокомпозитов.
Работа выполнена в рамках государственного задания ФАНО России (тема «Спин», № 01201463330 и Деформация, № 01201463327 ) и при частичной поддержке УрО РАН, проект № 15-9-2-12.
Библиографическая ссылка
Рубштейн А.П., Яковенкова Л.И., Медведева Д.С., Владимиров А.Б., Плотников С.А., Макарова Э.Б. ЧИСЛЕННЫЙ РАСЧЕТ МОДУЛЯ ЮНГА БИОКОМПОЗИТА С ИСПОЛЬЗОВАНИЕМ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ // Международный журнал прикладных и фундаментальных исследований. 2016. № 4-4. С. 680-685;URL: https://applied-research.ru/ru/article/view?id=9053 (дата обращения: 18.12.2025).