Проблема диагностирования и прогнозирования состояния здоровья является особенно актуальной в педиатрии, главной задачей которой является выявление патологий и хронических заболеваний на ранних этапах развития. Самым важным в жизни ребенка является грудной возраст, в котором большое значение придается его развитию в неонатальном периоде.
Часто в медико-биологических исследованиях складывается достаточно противоречивая ситуация. С одной стороны, накоплены большие массивы данных, отражающие различные встречающиеся в клинической практике ситуации, а с другой непропорционально малое количество информации, получаемое из их анализа. Кроме того, существует ряд факторов, учет которых является необходимым для выбора методов анализа биомедицинских данных.
Поэтому целью работы является обработка накопленных медицинских данных детей для прогнозирования состояния их здоровья при помощи математических методов.
Характеристика исследуемых данных
В качестве исходной информации для исследования использовались данные, полученные в НИИ акушерства и гинекологии Роддома № 4 г. Томска. Исходные данные представляют собой антропометрические, лабораторные и инструментальные (показатели кардиоинтервалографии (КИГ). В разные моменты времени оценивались ритмические характеристики т.е. временные промежутки сокращения сердца и характер распределения этих интервалов во времени.
Каждый показатель имеет физиологическое значение:
1. R-Rср (c) – среднее значение кардиоинтервалов RR;
2. dX (c) – вариационный размах длительности кардиоинтервалов. Определяется по формуле:
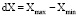 (1)
(1)
где Xmax и Xmin соответственно максимальное и минимальное значения длительности зарегистрированных интервалов RR. Отражает процесс регуляции синусовых сердечных ритмов, указывает на максимальную амплитуду колебаний сердечного ритма;
3. Sigma – среднее квадратическое отклонение, отражает среднюю амплитуду колебаний деятельности кардиоинтервалов RR, вычисляется по формуле:
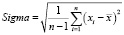 , (2)
, (2)
где xi – длина текущего зарегистрированного интервала RR;
4. Mo (c) – мода, наиболее часто встречающееся значение RR интервала, которое соответствует наиболее вероятному для данного периода времени уровню функционирования систем регуляции. Характеризует гуморальное звено регуляции сердечного ритма;
5. AMo ( %) – амплитуда моды, число значений интервалов, соответствующих Мо, выраженное в процентах. Отражает эффект стабилизации центральной регуляции на сердечный ритм;
6. Inap (intramuscular nerve action potential) – потенциал внутримышечного действия нерва (условные единицы).
7. IVR – индекс вегетативного равновесия. Характеризует степень централизации управления сердечным ритмом, вычисляется по формуле:
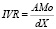 ; (3)
; (3)
8. ЧСС (уд/мин) – частота сердечных сокращений. Отражает интегральный уровень функционирования синусового узла;
9. PAPR – показатель адекватности процессов регуляции. Позволяет путем сопоставления с ЧСС судить о наличии избыточной или достаточной централизации управления ритмом сердца, вычисляется по формуле:
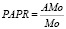 ; (4)
; (4)
10. VPR – вегетативный показатель ритма. Отражает состояние автономного уровня регулирования, вычисляется по формуле:
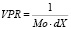 ; (5)
; (5)
11. NSR – напряженность сердечного ритма, является количественной оценкой процессов регуляции ритма сердца, вычисляется по формуле:
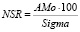 . (6)
. (6)
Для исследования используются показатели, измеренные в определенные интервалы времени: период беременности (Плод), на 1-ый, 3-ий, 5-ый, 30-ый день жизни.
Кубическая сплайн интерполяция
Заполнение пропусков в данных производилось с использованием кубической сплайн интерполяции (аппроксимации).
Сплайн-аппроксимация – приближенное представление функции или приближенное восстановление функции из заданного класса по неполной информации (напр., по значениям на сетке) с помощью сплайнов.
В его основе лежит следующая идея – интервал интерполяции разбивается на небольшие отрезки, на каждом из которых функция задается полиномом третьей степени. Коэффициенты полинома подбираются так, что на границах интервалов обеспечивается непрерывность функции, её первой и второй производных. Также есть возможность задать граничные условия – значения первой или второй производной на границах интервала. Если значения одной из производных на границе известны, то задав их, мы получаем крайне точную интерполяционную схему. Если значения неизвестны, то можно положить вторую производную на границе равно нулю и получить достаточно хорошие результаты.
Пусть заданы точки x1, x2, ..., xn и соответствующие им значения y1, y2, ..., yn функции f(x). На каждом из отрезков [xi, xk+1], k = 1, 2, ..., n-1 функцию приближаем при помощи полинома третьей степени:
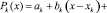
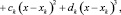 (7)
(7)
Для вычисления коэффициентов ak, bk, ck, dk, k = 1, 2, ..., n-1 решается система линейных уравнений, построенная из условия непрерывности производной P’(x) в узлах сетки и дополнительных краевых условий на вторую производную [3].
Анализ результатов исследования
Для решения задачи оценки уровня состояния здоровья детей были сформированы в соответствии со степенью тяжести следующие группы:
- 1 группа («Норма»), в которую вошло 119 детей с первой группой тяжести;
- 2 группа («Предкризис»), в которую вошло 12 детей со второй группой тяжести;
- 3 группа («Кризис»), в которую вошли 46 детей с третей группой тяжести.
Аппроксимация кубическим сплайном проводилась для всех исследуемых показателей. На рисунке (а, б, в) представлена сплайн-аппроксимация параметра RR.
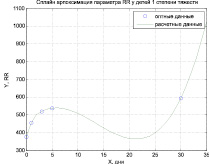
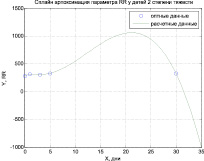
а) б)
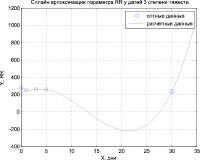
в)
Рис. Сплайн-аппроксимация параметра RR а) группа «Норма», б) группа «Предкризис», в) группа «Кризис»
Таблица 1
Коэффициенты кубической сплайн функции для параметра ЧСС
|
Показатели |
Коэффициенты |
Значения коэффициентов кубической сплайн– функции |
|||
|
0– 1 сутки |
1– 3 сутки |
3– 5 сутки |
5– 30 сутки |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Тяжесть 1 |
|||||
|
ЧСС |
a |
156,01 |
125,47 |
118,79 |
113,22 |
|
b |
– 46,37 |
– 16,97 |
1,28 |
– 6,54 |
|
|
c |
18,08 |
11,32 |
– 2,19 |
– 1,72 |
|
|
d |
– 2,25 |
– 2,25 |
0,08 |
0,08 |
|
|
Тяжесть 2 |
|||||
|
ЧСС |
a |
202,96 |
174,96 |
175,27 |
164,20 |
|
b |
– 45,61 |
– 13,14 |
2,48 |
– 12,92 |
|
|
c |
20,35 |
12,13 |
– 4,32 |
– 3,38 |
|
|
d |
– 2,74 |
– 2,74 |
0,16 |
0,16 |
|
|
Тяжесть 3 |
|||||
|
ЧСС |
a |
220,12 |
216,87 |
220,75 |
210,02 |
|
b |
– 7,72 |
0,31 |
– 0,09 |
– 10,22 |
|
|
c |
5,39 |
2,64 |
– 2,85 |
– 2,22 |
|
|
d |
– 0,91 |
– 0,91 |
0,10 |
0,10 |
|
Коэффициенты кубической сплайн функции были рассчитаны для всех исследуемых параметров. В табл. 1 представлены коэффициенты кубической сплайн функции для параметра ЧСС, аппроксимирующей зависимость показателей детей 1-3 группы тяжести.
Скорость и ускорение возрастных изменений показателей были рассчитаны для всех исследуемых показателей. В табл. 2–3 представлены скорость и ускорение для параметров RR и ЧСС.
Таблица 2
Скорость возрастных изменений показателей у детей
|
Возраст |
Rr |
ЧСС |
||||
|
Группа 1 |
Группа 2 |
Группа 3 |
Группа 1 |
Группа 2 |
Группа 3 |
|
|
0 |
104,96 |
56,74 |
– 49,49 |
– 46,37 |
– 45,61 |
– 7,72 |
|
1 |
59,05 |
12,92 |
– 9,92 |
– 16,97 |
– 13,14 |
0,31 |
|
3 |
15,03 |
– 4,52 |
9,17 |
1,28 |
2,48 |
– 0,09 |
|
5 |
4,04 |
21,68 |
– 9,62 |
– 6,54 |
– 12,92 |
– 10,22 |
|
30 |
60,13 |
– 186,89 |
120,39 |
55,83 |
110,29 |
74,25 |
Таблица 3
Ускорение возрастных изменений показателей у детей
|
Возраст |
Rr |
ЧСС |
||||
|
Группа 1 |
Группа 2 |
Группа 3 |
Группа 1 |
Группа 2 |
Группа 3 |
|
|
0 |
– 53,88 |
– 55,53 |
49,58 |
36,16 |
40,70 |
10,78 |
|
1 |
– 37,94 |
– 32,12 |
29,56 |
22,64 |
24,26 |
5,29 |
|
3 |
– 6,07 |
14,69 |
– 10,47 |
– 4,39 |
– 8,64 |
– 5,69 |
|
5 |
– 4,92 |
11,51 |
– 8,31 |
– 3,44 |
– 6,77 |
– 4,44 |
|
30 |
9,41 |
– 28,20 |
18,71 |
8,43 |
16,62 |
11,20 |
Заключение
В ходе выполнения работы произведена обработка накопленных медицинских данных детей, результатом чего стало проведение аппроксимации данных и вычисление коэффициентов кубических сплайнов. В работы произведена подробная характеристика исследуемых данных. Получены коэффициенты кубической сплайн функции, скорость и ускорение возрастных изменений показателей.
Библиографическая ссылка
Черкашина Ю. А. ПРИМЕНЕНИЕ КУБИЧЕСКОЙ СПЛАЙН ИНТЕРПОЛЯЦИИ В ЗАДАЧАХ ПРОГНОЗИРОВАНИЯ ФУНКЦИОНАЛЬНОГО СОСТОЯНИЯ ЗДОРОВЬЯ ДЕТЕЙ // Международный журнал прикладных и фундаментальных исследований. 2016. № 4-5. С. 887-890;URL: https://applied-research.ru/ru/article/view?id=9096 (дата обращения: 15.02.2026).

