При развитии газоснабжения России в малой энергетике все шире применяются газотрубные котлы малой и средней мощности, способствующие высокой степени автоматизации технологического процесса, обладающие простой конструкцией и не требующие больших материальных затрат на монтаж и дальнейшее обслуживание при эксплуатации. В связи с этим необходимо создание высокоэффективного котла малой мощности [1].
К процессу теплопереноса в топках данных котлов предъявляются высокие требования. Для правильной его организации необходимо владеть разноплановой информацией по процессам горения и теплообмена, и турбулентности.
Процесс горения в топках газотрубных котлов есть совокупность взаимообусловленных аэродинамических, тепловых и химических процессов. Температура, концентрация реагентов и другие величины изменяются как вследствие химических реакций, так и вследствие различных физических процессов: конвекции, диффузии, теплообмена излучением, поэтому химические и физические процессы нужно изучать совместно. Часто физические факторы оказывают определяющее влияние на полноту сгорания, условия воспламенения [1-2].
Цель исследования
Течение газов в технических устройствах почти всегда турбулентно. Исследование турбулентности является сложным разделом гидрогазодинамики. В процессах горения проблема турбулентности ещё более осложнена дополнительными факторами – химическими реакциями и излучением [1]. Основная задача работы заключается в подборе метода расчета турбулентных течений для определенных начальных условий, таких как сложная геометрическая форма расчетной области (топки газотрубного котла), и в получении наиболее точного результата.
Методы расчета турбулентных течений в топках котлов можно разделить на следующие: стационарный метод описания турбулентных течений реагирующих газов; применение статистической модели турбулентности; применение эмпирического коэффициента переноса в уравнениях турбулентных течений; применение модели турбулентности с двумя уравнениями.
Стационарный метод описания турбулентных течений реагирующих газов. Большинство течений, представляющих практический интерес, являются турбулентными. Турбулентные течения по своей природе нестационарные. Определенный опыт изучения подобных явлений в трубах, в пограничных слоях на стенках, в свободных струях и следах показывает, что в отдельных случаях можно пренебречь зависимостью турбулентного течения от времени [3, 4]. Значительные успехи достигнуты благодаря методам исследования, при которых турбулентные течения рассматриваются как стационарные ламинарные, а переносные свойства жидкости считаются переменными при переходе от одной точки к другой. Это позволяет разработать метод расчета стационарных течений независимо от того, являются они ламинарными или турбулентными [3, 4].
Рассматривать турбулентное течение как ламинарное с неоднородными свойствами – это не единственный способ описания турбулентных течений. Другой способ состоит в решении дифференциальных уравнений нестационарного движения в частных производных и расчете нерегулярного турбулентного движения.
Применение статистической модели турбулентности. Когда время всего процесса значительно больше времени турбулентных возмущений, то можно сказать, что турбулентное течение определяется средними характеристиками с добавлением переменных во времени характерных параметров.
В турбулентной модели видоизменяется стандартное уравнение Навье – Стокса за счет включения понятий среднего и возмущенного потока. Далее задаются параметры турбулентности. Коэффициенты молекулярного переноса заменяются на их эффективные величины: μeff = μ + μt (μeff, μt – эффективная и турбулентная вязкости). Для развитых турбулентных течений во всей области, за исключением регионов, непосредственно прилегающих к твёрдым границам, турбулентная вязкость намного больше, чем молекулярная вязкость, и μt существенно зависит от характеристик поля течения, при этом являясь переносимой величиной.
Подобные расчетные модели получили название статистических моделей турбулентности благодаря среднестатистическим величинам в уравнениях.
Решение системы уравнений с учетом вышеизложенного упрощает инженерные расчеты. Однако средние параметры включают в себя неизвестные – величины, связанные с флуктуацией. Эти величины, называемые турбулентными или напряжениями Рейнольдса, сложно точно определить.
Эмпирические коэффициенты переноса в уравнениях турбулентных течений. При рассмотрении турбулентного течения как течения газа, имеющего эффективную вязкость, эффективную теплопроводность и эффективный коэффициент диффузии, изменяющиеся от точки к точке, требуется решить вопрос об определении этих эффективных переносных свойств. Поэтому приведем обзор методов расчета эффективных переносных свойств при турбулентных течениях.
Наиболее известно определение эффективной вязкости турбулентного течения, которое дал Л. Прандтль [3, 4, 5]. Его гипотеза так называемого пути перемешивания позволяет рассчитывать турбулентную вязкость μt по уравнению
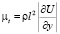 , (1)
, (1)
где ρ – местная плотность жидкости;
l – длина пути смешения;
U – скорость в направлении основного течения;
у – расстояние по нормали к этому направлению.
Уравнение (1) фактически подменяет вопрос об определении μt вопросом об определении l.
Таким образом, уравнение (1) вместе с некоторыми правилами определения l позволяет достаточно точно рассчитывать гидродинамические характеристики многомерных турбулентных потоков, при этом l изменяется при переходе от точки к точке гораздо в более узких пределах, чем μt.
Эффективную вязкость можно определить также по другим формулам. Например, Л. Прандтль [5] предположил, что свободные турбулентные течения можно описать с достаточной точностью, считая коэффициент μt постоянным по толщине пограничного слоя и равным
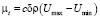 , (2)
, (2)
где δ – толщина слоя, а Umax и Umin – максимальная и минимальная скорости в некотором сечении слоя. Постоянная с имеет порядок 0,01, а плотность ρ, если она изменяется по сечению трубы, должна быть заменена некоторым средним значением.
При численных методах исследования течений жидкости с использованием гипотезы турбулентной вязкости допускается применять понятие коэффициента турбулентной тепловой диффузии λt (турбулентной теплопроводности) для моделирования процессов турбулентного переноса теплоты [6]. Данный коэффициент определяется выражением
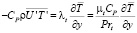 , (3)
, (3)
где Prt = (μtCP)⁄λt – турбулентное число Прандтля. Зная Prt, можно найти λt по вычисленным величинам μt [4]. Для пристеночных течений число Прандтля приблизительно равно 0,9; для плоских – 0,5 и для круглых струй – 0,7.
Тем не менее, обе эти формулы лишь с определенными ограничениями могут быть распространены на случай возвратных течений, в которых отсутствует одно доминирующее направление течения. Для них возможно применение гипотезы А.Н. Колмогорова [2] и Л. Прандтля [5], согласно которой коэффициент μt связан с кинетической энергией пульсационного движения k соотношением
μt = cρk0,5l, (4)
где l – местный масштаб турбулентности.
К достоинствам уравнения (4) и соответствующей ему модели турбулентности следует отнести возможность вывода дифференциального уравнения, в котором k будет играть роль основной зависимой переменной. В своих работах Ж.К. Ротта [3] предложил дифференциальное уравнение для масштаба турбулентности l. Оба эти дифференциальных уравнения являются эллиптическими. Для этих уравнений требуется эмпирическое определение постоянных, одна из которых c входит в уравнение (4), а другие появятся в дополнительных уравнениях, описывающих диссипацию и диффузию турбулентности. Кроме того, потребуются эмпирические данные об эффективных значениях коэффициентов теплопроводности и коэффициентов диффузии компонентов смеси.
Модели турбулентности с двумя уравнениями. Модели турбулентности с двумя уравнениями широко используются, так как они часто являются хорошим компромиссом между затратами на численное решение и точностью вычислений. Эти модели сложнее, чем рассмотренные ранее. Первым в этих моделях обычно является уравнение для кинетической энергии турбулентных пульсаций k. Вторым – уравнение переноса для масштаба турбулентности L, которая определяется разными методами. Широкое применение имеет модель Лаундера – Сполдинга [7], получившая название k-ε модели. Она базируется на уравнении переноса (транспортном уравнении) скорости диссипации энергии турбулентных пульсаций ε.
k-ε модель основывается на понятии эффективной величины вязкости μэфф. Турбулентная вязкость μt определяется выражением
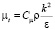 , (5)
, (5)
где Cμ – справочная константа.
В литературе также известны другие модели турбулентности с двумя уравнениями. Это и упомянутая ранее модель Ж.К. Ротта (k-kL) с уравнением переноса z = kL, и модели Д.К. Уилкокса, Ф.Р. Ментера (k-ω) с математическим выражением для турбулентной вязкости, связанной с турбулентной частотой ω через отношение
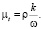 (6)
(6)
Одна из особенностей формулирования k-ω моделей – описание процессов в пристеночном слое при низких числах Рейнольдса.
Выводы
Рассмотренные выше методы расчета турбулентных течений, возможно, использовать при описании процессов турбулентного горения газообразного топлива. В настоящее время из представленных методов расчета турбулентных течений наиболее подходящей для топки с пассивным методом интенсификации процесса теплообмена является модель турбулентности с двумя уравнениями представленная k-ε модель.
Библиографическая ссылка
Батраков П.А. АНАЛИЗ МЕТОДОВ РАСЧЕТА ТУРБУЛЕНТНЫХ ТЕЧЕНИЙ В ТОПКАХ ГАЗОТРУБНЫХ КОТЛОВ // Международный журнал прикладных и фундаментальных исследований. 2016. № 4-6. С. 1053-1055;URL: https://applied-research.ru/ru/article/view?id=9131 (дата обращения: 02.01.2026).

