Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сбитнева С.А. 1

---

1 Южный федеральный университет

Основная идея, изложенная в предлагаемой статье, заключается обосновании того, что существующие методики финансового планирования обычно сосредотачиваются на какой-либо одной существующей проблеме и, как результат, не всегда в состоянии учесть все возможные последствия принимаемых управленческих решений. Это обстоятельство является следствием недооценки необходимости системного подхода к финансовому планированию как к процессу, который должен учитывать не только прямые последствия решений, но и опосредованное влияние этого решения на общее финансовое состояние предприятий. В статье представлена методика осуществления финансового планирования, основанная не на проводимых от случая к случаю расчетах, а на предварительно созданной экономико-математической модели бухгалтерского учета, включающей начисление налогов, и позволяющей оценивать финансовые последствия на микро-уровне, а также планируемые на будущее изменения на макро-уровне. Идеи, предложенные в работе, позволяют анализировать и прогнозировать воздействие финансового положения институциональной единицы в будущем.

Статья в формате PDF

1547 KB

матричная модель

финансовый учет

прогнозирование

ситуационно-матричное моделирование

1. Высотская А.Б. (2010). Налогообложение и бухгалтерский учет от папируса к матричному моделированию. Монография – Москва. Вузовская книга.

2. Высотская А. и Прокофьева М. (2013) Сложности преподавания МСФО в России. Бухгалтерское образование. May 2013, Vol. 28, No. 2, pp. 309–319.

3. Кольвах О.И. (2010). Ситуационно-матричная бухгалтерия в бухгалтерском учете и экономическом анализе. Монография – Москва. Вузовская книга.

4. Де Морган А. (1846).Элементы арифметики,пятое издание. Лондра: Тэйлор и Уолтон.

5. Дидье Леслер и Жан-ги Дего (1995). Матричный учет// Бернард, энциклопедия учета, контроля и регулирования и аудита. – С. 383.

6. Маттесич Р.(1964). Бухгалтерские и аналитические модели, Энглевуд Клиффс:Ирвин, C. 347–408.

7. Мефам М.Дж. (Осень 1988). Матричный учет – комментарий// Бухгалтерские и бизнес- исследования, часть 18 № 72, C. 375–378.

8. Сангстер А., МакКарти П. и Стонер Г. (2007). Уроки для аудитории от Луки Пачоли. Бухгалтерское образование, 22 (3).

9. Стонер Г. и Высотская А. (2012) Теория бухгалтерского учета с матрицами в Южном федеральном университете, Россия. Бухгалтерское образование. 27 (4). pp. 1019-1044.

Совершенно очевиден тот факт, что принятие своевременных и, главное, верных управленческих решений является жизненно важным для предприятий такого формата. Так, своевременное выявление финансовых затруднений и их диагностика имеет решающее значение, поскольку позволяет более безболезненно и действенно провести мероприятия, для их преодоления. Руководство любого предприятия нуждается в потоке информации для принятия информированных и разумных решений, влияющих на успех или неудачу его деятельности. Инвесторам нужна отчетность для анализа инвестиционного потенциала. Банкам требуется финансовая отчетность для принятия решения о выдаче кредитов, а многим компаниям отчетность необходима для определения риска, связанного с ведением коммерческой деятельности со своими клиентами и поставщиками. Поэтому формирование балансовых отчетов нарастающих итогом является актуальным направлением, поскольку всегда можно выделить тенденцию развития экономического субъекта в динамике.

Цель исследования

Учитывая тот факт, что все без исключения хозяйствующие субъекты применяют планирование и прогнозирование в современной предпринимательской практике, налицо необходимость разработки целостной, научно обоснованной концепции, основанной на аналитических методах, раскрывающей природу, сущность, способы осуществления планирования как неотъемлемой части деятельности хозяйствующего субъекта.

Текущие преобразования в экономической системе вызывают необходимость построения таких моделей, которые бы отвечали современным требованиям и условиям. Кроме того, как показывает практика, эпизодическое внимание хозяйствующих субъектов к планированию и прогнозированию крайне неэффективно. В этих условиях, налицо необходимость разработки системных, аналитических подходов к прогнозированию финансового состояния, как на административном уровне, так и на уровне хозяйствующих субъектов.

Материалы и методы исследования

В этой связи основополагающее значение приобретает метод ситуационно-матричного моделирования для целей прогнозирования финансового состояния предприятия. Существуя, как форма представления в виде универсального языка транзакций, через которые компактно и единообразно отображаются взаимоотношения субъектов экономики, взаимодействующих в различных организационных формах и на различных иерархических уровнях, позволяет раскрыть первоначальную структуру, лежащую в основе любой встречающейся на практике финансовой категории.

Поскольку проблема моделирования и прогнозирования представляет значительный теоретический и практический интерес, а применяемые в этой области методики нуждаются в существенных доработках, возникает необходимость его более детального анализа. Определяющую роль в решении названных проблем играет применение ситуационно-матричного моделирования в области финансового планирования и управления на предприятии, посредством чего возможен анализ результативности принимаемых управленческих решений, осуществление контроля эффективности управления, прогнозирование финансовых результатов и выявление резервов повышения эффективности финансового управления. Особое положение в данном контексте занимает возможность планирования последствий финансового состояния.

Балансовые уравнения играют ключевую роль в балансоведении, так как сами идеи ситуационно-матричного моделирования бухгалтерского учета распространены на решение тех задач и проблем, которые принято относить именно к нему. Эти уравнения представляют собой балансовые инварианты – сальдовые моментные уравнения.

Статическими называются уравнения, в которых не выделены в явной форме доходы и расходы, формирующие финансовый результат.

В отличие от статических, в динамических уравнениях происходит то самое выделение доходов и расходов или непосредственного финансового результата – прибыли или убытка. Таким образом, динамические уравнения показывают приращение (+,-) собственного имущества и капитала за истекший период.

В связи с этим, следует признать, что названия, статические и динамические уравнения, не совсем точно соответствуют их смыслу, если под динамикой понимать развертывание балансовых отчетов во времени, т.е. последовательные состояния баланса институционной единицы на каждый момент времени.

Вместе с тем, статические и динамические уравнения, рассматриваемые обычно в работах по балансоведению, – это итоговые скалярные уравнения, принимаемые без доказательства как постулаты.

Исходное матричное уравнение баланса для любых группировок счетов определяется как разность:

В – В' = DВ, (1)

где получаемая таким образом сальдовая матрица DВ, как и ранее рассмотренная, зеркально симметрична и сумма ее элементов всегда равна нулю.

Исходная матричная модель формирования статического АП – уравнения будет выглядеть следующим образом:

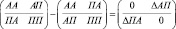, (2)

где АА – активно-активный, АП – активно-пассивный, ПА – пассивно-активный, ПП – пассивно-пассивный оборот между макросчетами балансового отчета. Чертой в записи матриц отделён актив от пассива.

В результате матрично-векторного преобразования получаем (b – b'=Db):

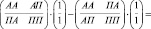
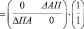, (3)

откуда

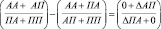, (4)

или

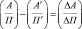. (5)

Формирование компонентов векторов статического АП-уравнения представлены в табл. 1.

Таблица 1

Формирование компонентов векторов статического АП-уравнения

В результате векторно-скалярного преобразования сальдового вектора, умножением его слева на единичную вектор-строку, получаем:

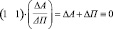(6)

Преобразования над исходным матричным уравнением является матричной моделью формирования статического балансового уравнения в его конечной, т.е. скалярной (числовой) форме.

Так как в рамках настоящего примера невозможно рассмотрение исходных данных в виде соответствующего шахматного баланса сводных макропроводок за весь период существования предприятия, а имеется только оборот, равный в один год, то данное статическое уравнение будет рассмотрено в матрично-векторной форме и будет определено как:

Dbt-1+ b – b'=Dbt (7)

или

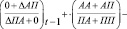
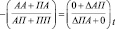(п. К), (8)

откуда

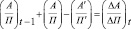. (9)

Представим наглядно статическое уравнение в матрично-векторной форме (табл. 2).

Таблица 2

Статическое АП-уравнение в матрично-векторной форме

В результате векторно-скалярного преобразования сальдового вектора, умножением его слева на единичную вектор-строку, получаем:

ΔА + ΔП ≡ 58000,00 + 5056783,86 + 223000,00 + + 2000,00 + (– 100568,51) + 1177272,18 + (– 16487,53) + + (– 22393,76) + ( – 844376,25) + 721393,76 + 2667376,25 + + (– 53278,30) + 81470,00 + 45237,16 + (– 217032,58) + + 7259,76 + 720720,00 + 1741882,04) + (– 31796,19) + + 403721,14 + 109204,82 + (– 1176993,92) + 16310,69 + + 22393,76 + 844693,49 + (– 2513791,87) + (– 12000,00) + + (– 984415,38) + (– 20032,53) + (– 123415,00) + + (– 46706,49) + (– 406044,56) + (– 17874,00) + + (– 5569630,00) + (– 1741882,04) ≡ 0.

Так как дебетовое сальдо пассива всегда равно его кредитовому сальдо, взятому с противоположным знаком, т.е. DП = – DП' (где DП – дебетовое, а DП' – кредитовое сальдо пассива), то из этого следует: DА – DП' ≡ 0. Отсюда имеем статическое АП – уравнение как тождественное равенство итогового дебетового сальдо актива и кредитового сальдо пассива: DА ≡ DП'. Переобозначив: А = DА и П = DП', имеем в традиционном виде тождество: А ≡ П.

Построим динамическое АП-уравнение, используя обороты за 2012 год. Для этого выделим из состава пассива счета доходов (Д), из состава активов – счета расходов (Р). Следует отметить, что суммы макропроводок по корреспонденциям макросчетов актива и пассива динамического АП – уравнения будут отличаться от соответствующих им сумм статического АП-уравнения на суммы проводок со счетами доходов и расходов. Соответствующая моделеообразующей матрице, исходная матричная модель формирования динамического АП – уравнения представлена следующим образом (п. Л):

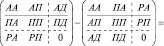
(10)

Счета доходов и счета расходов – это разные счета даже, если они представлены в плане счетов как смешанные. Соответствующие разности оборотов по этим счетам имеют смысл финансового результата.

Корреспонденции доходов – макропроводки с счетами А и П имеют следующий смысл: B(A,Д) = AД – доходы в активах, т.е. доходы, связанные с соответствующим увеличением активов; B(П, Д) = ПД – доходы в пассивах, например, доходы, от выполнения – уменьшения обязательств, например, при учете доходов по методу начислений, с использованием счета 62. Смысл корреспонденций расходов: B(Р,A) = РA – расходы в активах; B(Р,П) = РП – расходы в пассивах, т.е. расходы с одновременным увеличением пассива.

Матрично-векторное преобразование выполнено умножением справа не на единичный вектор e, как обычно, а умножением – на вектор e0. Финансовый результат в форме инвертированной («дебетовой») прибыли: DРД = Р – Д, или прибыли, показываемой с отрицательным знаком, и убытка – с положительным знаком, попадает в нижнюю часть сальдового вектора, т.е. в пассив баланса, как это видно из приводимого ниже результата матрично-векторного преобразования.

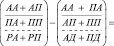
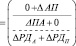(11)

Формирование компонентов векторов динамического АП-уравнения представлено в табл. 3.

Таблица 3

Формирование компонентов векторов динамического АП-уравнения

Представим наглядно динамическое АП-уравнение в матрично-векторной форме (табл. 4).

Таблица 4

Динамическое АП-уравнение в матрично-векторной форме

Результаты исследования и их обсуждение

Так, с помощью формул матричного учета можно вести бухгалтерский учет точно так же, как и с помощью известных учетных процедур или обычных компьютерных программ бухгалтерского учета. Стоит отметить, что многие компьютерные программы направлены на то, чтобы пользователь, не используя сложные программные продукты для анализа данных бухгалтерского учета, осуществлял подготовку отчетов в базах данных. Ключевой аспект применения прогнозного балансового отчета на практике основан на особенностях составления всех бюджетов. Бюджет – это годовой финансовый план предприятия. Он состоит в основном из прогнозного отчета о прибылях и убытках, прогнозного балансового отчета и кассового плана. По сути, бюджет составляется практически аналогично матричному прогнозному балансовому отчету. Поскольку в основе обоих лежат выбранные прогнозные ключевые целевые показатели, нормативы, нормы. Путем установления параметров и лимитов по размеру и структуре дебиторской задолженности, нормативов по остаткам сырья, материалов и готовой продукции на складах, по размеру и сроку кредиторской задолженности определяются основные статьи прогнозных балансов, а, следовательно, и бюджетов. Можно смело утверждать, что прогнозный балансовый отчет, сформированный с использование формул ситуационно-матричного моделирования, – это отчет, который дает возможность пользователю рассмотреть наиболее ожидаемое финансовое состояние, ожидаемые финансовые результаты экономической единицы.

Жизнеспособность рассматриваемой модели придает возможность осуществления анализа значения выбранного глобального целевого показателя (будь то объем выпускаемой продукции, сформированная себестоимость продукции, прибыли и т.д.) на основе локальных коэффициентов целевого показателя (структура затрат), которые рассчитываются в относительных величинах. Таким образом, возможно изменяя данные, к примеру, структуры затрат, рассчитывать новые локальные коэффициенты и составлять новые балансовые отчеты в относительных величинах. Впоследствии совершать различные преобразования, в результате которых возможно получать различные варианты балансовых отчетов, показатели которых будут характеризовать будущее финансовое состояние экономического субъекта.

Модель формирования нарастающих итогов в балансовых отчетах на основе матричного учета направлена на прогнозирование развития предприятия в динамике.

Заключение

Прежде всего, стоит отметить, что данная модель прогнозирования является новым перспективным направлением в анализе данных бухгалтерского учета и интерпретировать ее можно по-разному. Основным и важным шагом в создании метамодели для целей прогнозирования является необходимость составления матрицы дебетовых оборотов, а впоследствии совершение различных преобразований, в результате которых необходимо получить различные варианты балансовых отчетов, показатели которых будут характеризовать будущее финансовое состояние субъекта экономической деятельности. Рассмотренная модель формирования прогнозных балансовых отчетов является перспективным направлением для осуществления планирования и прогнозирования выбранных управленцем целевых показателей. Можно просмотреть структуру затрат в локальных коэффициентах целевого показателя и впоследствии меняя значения подобных коэффициентов, анализировать прогнозную себестоимоть продукции. Переход к обычному представлению балансовых отчетов в денежных единицах осуществляется умножением содержимого отчетов в приведенных единицах λX,Y на прогнозируемое значение целевого показателя Qпрогн. или прогнозную себестоимость продукции в предстоящем периоде.

Моделируя балансовые отчеты по нарастающим итогам, можно рассмотреть переход от констатации конкретных фактов хозяйственной деятельности по периодам к моделированию по нарастающим итогам. Применяя формулы ситуационно-матричного моделирования и суммируя отдельные составляющие главной книги нарастающим итогом, получается, формировать итоги не по каждому периоду в отдельности, а рассматривать динамику наращения остатков по счетам и производить анализ наращения остатков по счетам.

Применение подобной модели на практике не требует каких-либо материальных затрат. Главное – управленцем выбрать для анализа необходимые данные для рассмотрения прогнозного целевого показателя, а также применить элементарный алгоритм построения матричной модели для целей прогнозирования.

Возможно, что эта модель в бухгалтерском учете является лишь новым перспективным направлением развития прогнозирования и планирования деятельности экономической единицы, но уже сейчас в подобном виде она жизнеспособна для тех лиц, которые знают элементарные формулы матричной алгебры и которые способны их применять в бухгалтерском учете, поскольку алгоритм составления данной модели описан в полной мере детально и прозрачно. Составление прогнозного баланса на основе ситуационно-матричного моделирования дает возможность менеджерам контролировать изменения ключевых его параметров.

Библиографическая ссылка