Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Снегирева Л.В. 1

---

1 ГБОУ ВПО «Курский государственный медицинский университет Минздрава России»

В статье проведена оценка эффективности формирования математической компетентности учащихся факультета клинической психологии, изучена динамики развития способностей к математическому анализу и синтезу, логическому умозаключению, математическому обобщению студентов-психологов на различных этапах обучения в медицинском вузе. Авторами показано, что в курсе изучения математики студентами медицинского вуза происходит формирование знаний, необходимых в дальнейшей профессиональной деятельности будущих психологов, идет активное развитие математических способностей учащихся. Надежным критерием сформированности математической компетентности студентов – психологов выступают оценки курсового экзамена по дисциплине «Математика». А сама математическая компетентность является востребованным инструментом изучения специальных дисциплин студентами факультета клинической психологии.

Статья в формате PDF

1554 KB

математическая компетентность

критерии

обучение

эффективность

динамика

1. Митина О.В. Математические методы в психологии: практикум. – М.: Аспект-Пресс, 2008. – 238 с.

2. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь», 2003. – 350 с.

3. Федеральный государственный образовательный стандарт высшего профессионального образования по направлению подготовки (специальности) 030401 Клиническая психология (квалификация (степень) «специалист») / Минобрнауки России. – М., 2010. – 49 с.

Общепризнанным является факт тесной и многоплановой связи между науками «Психология» и «Математика». Традиционным стало применение математических методов в психологии, в особенности различных статистических методов, при анализе и обработке данных эксперимента. Использование математических методов, в значительной степени объективизирует выводы психологов, позволяет вычленить из огромного набора разрозненных психологических данных важные в том или ином смысле факторы и переменные, оказывающие наибольшее влияние на исследуемый результирующий признак [1, 2].

В этой связи становится понятным внимание, которое уделяют в современной высшей школе формированию математической компетентности как составной части профессиональной компетентности будущего психолога, развитию математических способностей к анализу, синтезу, логическому умозаключению.

Актуальность проблемы объективной оценки уровня сформированности математических способностей учащихся факультета клинической психологии, а также динамики развития указанных способностей, определяется пониманием того факта, что успешность профессиональной деятельности обусловлена в значительной степени математической компетентностью психолога [3].

Целью нашего исследования стало изучение уровня сформированности математических способностей у студентов факультета клинической психологии на различных этапах обучения в медицинском вузе.

Работа осуществлялась на базе Курского государственного медицинского университета. В исследования приняли участие студенты первого, второго и четвертого курсов факультета клинической психологии.

Задачи исследования были определены в следующем объеме:

1. Изучить уровень развития математических способностей у студентов младших курсов факультета клинической психологии на различных этапах изучения дисциплины «Математика»

2. Сопоставить полученные результаты с академической успеваемостью по предмету «Математика».

3. Проанализировать уровень математической компетентности студентов старших курсов факультета клинической психологии.

В рамках решения поставленных задач было проведено тестирование 51 учащегося младших и старших курсов факультета клинической психологии. Для обеих групп поддерживались константные условия: исследование проводилось в первой половине дня (11:00), в учебной комнате, длительность исследования составила 20 минут, исследуемые выполняли методику самостоятельно, использование электронных устройств запрещалось.

Для исследования использовался специальный тест, созданный на основе теста структуры интеллекта Атмхауэра, включающего в себя шкалу определения математических способностей.

Каждое задание теста ставило перед испытуемым строго определенную цель, для достижения которой студенту необходимо было использовать способности к логическому умозаключению.

В целях успешного решения задачи субъект должен был предварительно ориентироваться в ее условии, то есть выделить различные элементы в ее структуре, дать им различную оценку, систематизировать их, определить их иерархию. Осуществление этих операций требовало наличия высокого уровня аналитических способностей.

Кроме аналитических способностей, ориентировка в условиях математической задачи предполагала высокую степень развития синтетических способностей, т.к. выявленные элементы необходимо объединить в комплексы, отыскать математические отношения и функциональные зависимости между ними.

На следующем этапе с учетом выявленных существенных отношений решающим вырабатывалась гипотеза относительно характера стратегии решения, которая в математической деятельности всегда носит обобщенный характер. Таким образом, стратегия решения в математической деятельности всегда носит обобщенный характер. Таким образом, успешное выполнение задач данного субтеста являлось свидетельством развитой способности у испытуемого к математическому анализу и синтезу, логическому умозаключению, математическому обобщению.

Результаты исследования и их обсуждение

В результате проведенной диагностики широкого спектра мыслительных операций испытуемых нам удалось ранжировать студентов в соответствии с уровнем развития математических способностей (табл. 1). Использовались шкалы ранжирования по четырем группам: высокий уровень развития математических способностей, средний, средне-низкий и низкий уровень сформированности математических способностей обучаемых.

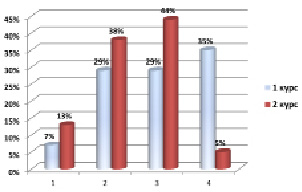
Рис. 1. Распределение студентов младших курсов по степени развития математических способностей. Примечание: 1 – высокая (7 % на первом курсе и 13 % на втором курсе); 2 – средняя (29 % на первом курсе и 38 % на втором курсе); 3 – средне-низкая (29 % на первом курсе и 44 % на втором курсе); 4 – низкая (35 % на первом курсе и 5 % на втором курсе)

Таблица 1

Распределение студентов-психологов младших курсов в соответствии с уровнем развития математических способностей

Как видно из табл. 1, на первом курсе число учащихся, показавших высокую степень математических способностей к анализу и синтезу, составило 7 %. Среднюю способность к логическому умозаключению продемонстрировали 29 % первокурсников, а средне-низкий и низкий уровень способностей к математическому обобщению были выявлены у 29 % и 35 % учащихся соответственно.

На следующем этапе нашего исследования мы проверили уровень сформированности математической компетентности учащихся после курса высшей математики, изученного в вузе. Для этого мы провели анализ тестирования студентов второго курса факультета клинической психологии. Из табл. 1 видно, что число учащихся второго курса, показавших высокую степень математических способностей к анализу и синтезу, после изучения математики составило 13 %, что на 6 % выше показателя первого курса.

После освоения курса математики в вузе возросло количество студентов, показавших результаты, соответствующие среднему уровню развития способностей к логическому умозаключению. Среди студентов первого курса нам удалось выявить 29 % таких учащихся, а на втором курсе уже 38 % студентов продемонстрировали средние способности к анализу и синтезу.

Положительная динамика была отмечена в группе учащихся, отнесенных к средне-низкому уровню развития математических способностей. В ходе изучения курса математики с 29 % на первом курсе до 44 % на втором курсе выросло число студентов, чьи логические способности обеспечили им место в группе со средне-низким уровнем развития способностей к математическому обобщению.

Расширение двух предыдущих групп: группы студентов со средними и средне-низкими способностями произошло за счет уменьшения числа студентов, демонстрировавших изначально низкий уровень развития математических способностей. Так, количество студентов показавших низкую способность к анализу уменьшилась с 35 % на первом курсе до 5 % втором курсе.

Далее нами было запланировано сопоставление результатов тестирования с итогами оценки академической успеваемости испытуемых с использованием корреляционного анализа по методу Спирмена. Нами были учтены как оценки на курсовом экзамене по математике, так и средний балл текущей успеваемости студентов. Результаты проведенного анализа представлены в табл. 2.

Таблица 2

Сопоставление результатов тестирования с итогами оценки академической успеваемости студентов

Полученные данные позволяют говорить о наличии положительной корреляции между результатами проведенного теста изучения математических способностей учащихся и академической успеваемостью испытуемых, что позволяет нам в дальнейшем использовать оценки курсового экзамена в качестве надежного критерия сформированности математической компетентности.

Таблица 3

Распределение студентов различных курсов по степени развития математических способностей

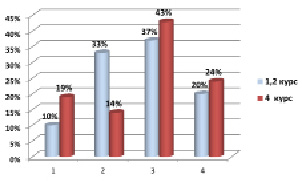
Рис. 2. Распределение студентов различных курсов по степени развития математических способностей. Примечание: 1 – высокая (10 % на младших курсах и 19 % у старшекурсников); 2 – средняя (33 % на первом-втором курсах и 14 % на четвертом курсе); 3 – средне-низкая (37 % на младших курсах и 43 % у старшекурсников); 4 – низкая (20 % на первом-втором курсах и 24 % на четвертом курсе)

Диагностируя на следующем этапе исследования математические способности студентов-старшекурсников, мы попытались понять, насколько востребованы формируемые нами у учащихся математические способности в процессе изучения специальных дисциплин (табл. 3).

Оказалось, что студенты-психологи активно используют математические навыки к анализу данных в процессе обучения. Об этом свидетельствуют результаты тестирования (табл. 3).

На четвертом курсе число студентов, продемонстрировавших средне-низкий уровень развития математических способностей возросло на 6 % по сравнению с показателями студентов младших курсов. А число студентов с низким уровнем развития способностей к анализу и синтезу осталось практически неизменным. Уменьшилось количество студентов в группе со средними показателями с 33 % до 14 % за счет перехода в группу с высокими математическими способностями. На 9 % возросло число учащихся с высокими показателями способности к логическому умозаключению.

Полученные в результате исследования данные позволяют нам сделать вывод о том, что в курсе изучения математики студентами медицинского вуза происходит не только формирование знаний, необходимых в дальнейшей профессиональной деятельности будущих психологов, но и идет активное развитие математических способностей учащихся.

Надежным критерием сформированности математической компетентности студентов – психологов выступают оценки курсового экзамена по дисциплине «Математика». А сама математическая компетентность является востребованным инструментом изучения специальных дисциплин студентами факультета клинической психологии и залогом успешности в будущей профессии.

Библиографическая ссылка