Использование параллельных модульных кодов позволяет не только повысить скорость обработки данных, но обеспечить свойство отказоустойчивости специализированным вычислительным устройствам, функционирующих в реальном масштабе времени. Среди модульных кодов занимают коды полиномиальной системе классов вычетов (ПСКВ). Данные коды, обладая свойством арифметичности, позволяют строить отказоустойчивые спецпроцессоры, которые способны сохранять работоспособное состояние за счет снижения в допустимых пределах основных показателей качества. Чтобы обеспечить коррекцию результата в кодах используют позиционные характеристики (ПХ), которые позволяют определить местоположение и глубину ошибки. Разработка и модификация методов вычисления позиционной характеристики – интервальный номер, позволят выполнять коррекцию результата при меньших аппаратных и временных затратах, что является актуальным.
В работе рассмотрен метод вычисления позиционной характеристики – интервальный номер. Данная позиционная характеристика позволяет осуществлять поиск и коррекцию ошибок в кодах ПСКВ. С целью снижения схемных затрат на реализацию проведены модификации этого метода. Разработанные модификации метода вычисления интервального номера в кодах ПСКВ позволили снизить схемные затраты на 3-5 % по сравнению с классическим методом уже при обработке 15-разрядных данных.
Параллельные непозиционные коды являются базой для построения отказоустойчивых специализированных вычислительных устройств, функционирующих в реальном масштабе времени [1-3]. Коды полиномиальной системе классов вычетов (ПСКВ), обладая свойством арифметичности, позволяют строить отказоустойчивые спецпроцессоры, которые способны сохранять работоспособное состояние за счет снижения в допустимых пределах основных показателей качества. Чтобы обеспечить коррекцию результата в кодах используют позиционные характеристики (ПХ), которые позволяют определить местоположение и глубину ошибки. Разработка и модификация методов вычисления позиционной характеристики – интервальный номер, позволят выполнять коррекцию результата при меньших аппаратных и временных затратах, что является актуальным.
В коде ПСКВ позиционный двоичный код, представляется в полиномиальной форме, а затем этому полиному в соответствие ставится набор остатков [4-6]
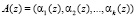 , (1)
, (1)
где 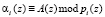 ; pi(z) – неприводимые полиномы поля GF(2); i = 1,…, k.
; pi(z) – неприводимые полиномы поля GF(2); i = 1,…, k.
Этот набор оснований кода ПСКВ образует рабочий диапазон системы
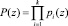 , (2)
, (2)
Так как сравнения по одному и тому же модулю можно почленно складывать, то для двух полиномов
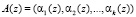 и
и 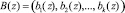 , справедливо
, справедливо
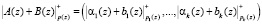 , (3)
, (3)
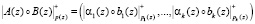 , (4)
, (4)
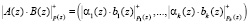 . (5)
. (5)
где + и  – операция суммирования и вычитания по модулю р.
– операция суммирования и вычитания по модулю р.
Параллельная и независимая обработка остатков служат идеальной основой для коррекции ошибок, возникающих из-за сбоев в работе системы [7]. При этом в кодах ПСКВ не происходит обмен данных между модулями. Это свойство кодов ПСКВ используют для обнаружения и коррекции ошибки. Но для этого необходимо ввести контрольные основания.
Введение r контрольных оснований ПСКВ, которые должны удовлетворять условию
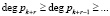
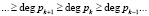 , (6)
, (6)
приводит к расширению рабочего диапазона до полного диапазона
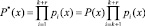 . (7)
. (7)
В основу большинства алгоритмов и методов поиска и коррекции ошибок в модулярных кодах положена процедура вычисления позиционной характеристики. Поскольку ошибка переводит правильный 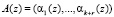 в полином
в полином 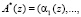
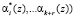 , лежащий вне рабочего диапазона, то, зная номер интервала, куда попал искаженный полином
, лежащий вне рабочего диапазона, то, зная номер интервала, куда попал искаженный полином 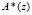 , можно определить основание, по которому произошла ошибка, а также ее глубину. Таким образом, для определения местоположения полинома, представленного кодом ПСКВ, требуется вычисление позиционной характеристики (ПХ). При этом немодульные операции определения ПХ необходимо заменить модульными операциями, которые успешно реализуются в модулярных кодах [6-10].
, можно определить основание, по которому произошла ошибка, а также ее глубину. Таким образом, для определения местоположения полинома, представленного кодом ПСКВ, требуется вычисление позиционной характеристики (ПХ). При этом немодульные операции определения ПХ необходимо заменить модульными операциями, которые успешно реализуются в модулярных кодах [6-10].
Данное свойство модулярных кодов и предопределило повышенный интерес разработчиков к позиционной характеристике – интервальный номер полинома lинт(z). Процесс определения данной характеристики осуществляется согласно выражения
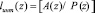 . (8)
. (8)
Несмотря на то, что процедура (8) относится к немодульным, ее сводят к совокупности модульных операций. В работе [6] представлено устройство, осуществляющее обнаружение и коррекцию ошибки в модулярном коде на основе вычисления интервального номера. В основу данного алгоритма положено свойство подобия ортогональных базисов полной, содержащей контрольные основания, и безизбыточной ПСКВ, согласно которому
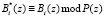 , (9)
, (9)
где Bi*(z) и Bi(z) – ортогональные базисы безизбыточной и полной системы.
Тогда имеем
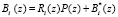 (10)
(10)
где 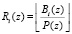 .
.
Подставив последнее равенство в выражение (8) получаем
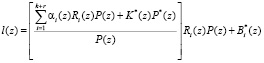 . (11)
. (11)
где K(z) – ранг полной системы оснований ПСКВ.
Так как множество значений интервального номера lинт(z) представляет собой кольцо по модулю Pконт(z), то выражение (11) преобразуется к виду
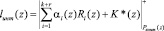 , (12)
, (12)
где ранг безизбыточной системы определяется выражением
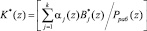 . (13)
. (13)
Если lинт(z) = 0, то исходный полином А(z) лежит внутри рабочего диапазона и не является запрещенным. В противном случае А(z) – ошибочная комбинация. В табл. 1 представлены номера интервалов, в которые попадают ошибочные полиномы Al*(z),при возникновении однократной ошибки по основаниям ПСКВ. При этом полиномы p1(z) = z + 1, p2(z) = z2 + z + 1 и p3(z) = z4 + z3 + z2 + z + 1 являются рабочими основаниями. В качестве контрольных оснований выбраны полиномы p4(z) = z4 + z3 + 1 и p5(z) = z4 + z + 1.
Таблица 1
Распределение однократных ошибок кода ПСКВ в GF(24)
|
Основание ПСКВ |
Глубина ∆ai(z) |
Интервал, представленный в полиномиальной форме |
|
p1(z) = z + 1 |
1 |
z7 + z4 + z2 + z |
|
p2(z) = z2 + z + 1 |
1 |
z7 + z5 + z2 + z + 1 |
|
z |
z7 + z6 + z5 + z4 + z2 |
|
|
p3(z) = z4 + z3 + z2 + z + 1 |
1 |
z7 + z4 + z3 + z + 1 |
|
z |
z7 + z3 + z + 1 |
|
|
z2 |
z7 + z5 |
|
|
z3 |
z7 + z6 + z5 + z4 + z3 + z + 1 |
|
|
p4(z) = z4 + z3 + 1 |
1 |
z7 + z4 + z3 |
|
z |
z7 + z3 + z + 1 |
|
|
z2 |
z7 + z5 + z3 + z2 |
|
|
z3 |
z7 + z6 + z5 + 1 |
|
|
p5(z) = z4 + z + 1 |
1 |
z5 + z4 + z |
|
z |
z6 + z5 + z2 |
|
|
z2 |
z7 + z6 + z3 |
|
|
z3 |
z5 + z3 + z + 1 |
Очевидно, что по величине lинт(z) можно однозначно определить местоположение и глубину  ошибки. В табл. 2 представлены схемные затраты на реализацию алгоритма (12), используемого для вычисления интервального номера.
ошибки. В табл. 2 представлены схемные затраты на реализацию алгоритма (12), используемого для вычисления интервального номера.
Таблица 2
Схемные затраты для устройства вычисления интервального номера при реализации алгоритма (12)
|
Разрядность сумматоров |
GF(23) |
GF(24) |
GF(25) |
|
|
Количество сумматоров |
5 |
2 |
1 |
|
|
6 |
2 |
3 |
||
|
7 |
1 |
|||
|
8 |
3 |
|||
|
12 |
2 |
|||
|
16 |
1 |
|||
|
18 |
2 |
|||
|
19 |
2 |
|||
|
21 |
3 |
|||
|
Количество нейронов с учетом первого слоя |
17 |
52 |
139 |
|
Анализ выражения (12) показывает, что применение составного модуля Рконт(z), по которому определяется значение интервального номера lинт(z), с точки зрения аппаратурных затрат, является не самым оптимальным. Это обусловлено тем, что одномерные исчисления над кольцом ZРконт по формуле (12) требует обработки log2 Рконт(z) – разрядных операндов.
Использование изоморфизма, порожденного китайской теоремой об остатках (КТО), позволяет перейти от одномерной обработки к многомерной. Приравнивая соответствующие значения Рконт(z) и оснований 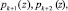
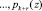 , получаем r преобразований
, получаем r преобразований
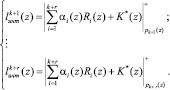 (14)
(14)
Проведем расчет аппаратурных затрат необходимых для реализации данного нейроподобного вычислительного устройства. Полученные данные сведены в табл. 3.
Таблица 3
Схемные затраты для устройства вычисления интервального номера при реализации алгоритма (14)
|
Разрядность сумматоров |
GF(23) |
GF(24) |
GF(25) |
|
|
Количество сумматоров |
2 |
1 |
||
|
3 |
1 |
|||
|
4 |
1 |
2 |
||
|
5 |
1 |
|||
|
6 |
3 |
|||
|
7 |
1 |
|||
|
8 |
2 |
|||
|
10 |
1 |
|||
|
12 |
3 |
|||
|
16 |
2 |
|||
|
18 |
2 |
|||
|
19 |
1 |
|||
|
22 |
1 |
|||
|
Количество нейронов |
7 |
32 |
99 |
|
|
Количество нейронов с учетом первого слоя |
14 |
47 |
130 |
|
Анализ таблицы показывает, что применение данной модификации метода вычисления интервального номера в кодах ПСКВ позволяет сократить схемные затраты по сравнению с алгоритмом (12). Так как кода ПСКВ, использующего неприводимые полиномы поля 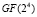 , схемные затраты сократились на 9,8 % по сравнению с реализацией согласно (12). Однако данная модификация метода вычисления позиционной характеристики не позволила достичь минимальных схемных затрат. Это связано в необходимостью реализации немодульной процедуры – вычисления ранга K(z), что в конечном счете снижает скорость работы устройства и его надежность.
, схемные затраты сократились на 9,8 % по сравнению с реализацией согласно (12). Однако данная модификация метода вычисления позиционной характеристики не позволила достичь минимальных схемных затрат. Это связано в необходимостью реализации немодульной процедуры – вычисления ранга K(z), что в конечном счете снижает скорость работы устройства и его надежность.
Решить данную проблему можно за счёт модификации алгоритма вычисления интервального номера. В основу данной модификации положено свойство – отсутствие переноса единицы из младшего разряда в старший при выполнении арифметической операции сложения двух операндов в расширенных полях Галуа GF (2v). Таким образом, величина ранга K*(z) безизбыточной системы ПСКВ p1(z),…, pk(z) определяется значением 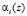 и
и 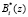 , и никоим образом не зависит от переполнения рабочего диапазона P(z). Следовательно, вычислив
, и никоим образом не зависит от переполнения рабочего диапазона P(z). Следовательно, вычислив 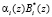 modPраб(z), можно отказаться от вычисления K*(z) и перейти к двухслойной организации нейронной логики. Тогда (14) примет вид
modPраб(z), можно отказаться от вычисления K*(z) и перейти к двухслойной организации нейронной логики. Тогда (14) примет вид
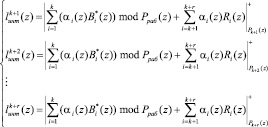 (15)
(15)
Схемные затраты, необходимые на реализацию модификации метода вычисления интервального номера в кодах ПСКВ, представленного равенством (15), сведены в табл. 4.
Таблица 4
Схемные затраты для устройства вычисления интервального номера при реализации алгоритма (15)
|
Разрядность сумматоров |
GF(23) |
GF(24) |
GF(25) |
|
|
1 |
4 |
|||
|
Количество сумматоров |
2 |
1 |
4 |
2 |
|
3 |
1 |
4 |
3 |
|
|
4 |
1 |
2 |
3 |
|
|
5 |
1 |
2 |
||
|
6 |
1 |
|||
|
7 |
||||
|
8 |
8 |
|||
|
10 |
1 |
|||
|
14 |
1 |
|||
|
Количество нейронов с учетом первого слоя |
14 |
44 |
115 |
|
Анализ таблицы показывает, что реализация модификации метода вычисления интервального номера согласно (15) позволяет понизить схемные затраты на 3-5 % в зависимости от размерности поля Галуа. При этом при увеличении размерности кода ПСКВ схемные затраты сокращаются в больших процентах.
Дальнейшее совершенствование алгоритмов вычисления данной позиционной характеристики возможно за счет использования потенциальных возможностей алгебраической системы ПСКВ.
Выводы
Использование кодов полиномиальной системы классов вычетов позволяет не только повысить скорость обработки сигналов, но и обеспечить специализированному вычислительному устройству свойство – устойчивость к отказам, возникающим в процессе функционирования. В статье рассмотрены модификации метода вычисления позиционной характеристики интервальный номер. Полученные результаты свидетельствуют о том, что разработанные модификации позволяют уменьшить схемные затраты на выполнения этой немодульной операции, что позитивно скажется на надежности работы непозиционного спецпроцессора класса вычетов.
Библиографическая ссылка
Велигоша А.В., Калмыков И.А., Корниенко Р.С., Ряднов С.А. МЕТОД ВЫЧИСЛЕНИЯ ИНТЕРВАЛЬНОГО НОМЕРА В МОДУЛЯРНЫХ КОДАХ И ЕГО МОДИФИКАЦИЯ // Международный журнал прикладных и фундаментальных исследований. 2016. № 5-3. С. 400-405;URL: https://applied-research.ru/ru/article/view?id=9263 (дата обращения: 07.03.2026).

