Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Хачaтрян С.А. 1

---

1 ФГБОУ ВО «Московский государственный машиностроительный университет (МАМИ)»

Разработать математическую модель отдельного конвейера и в цепи конвейерной системы шахты, позволяющую рассчитать основные показатели их надежности в любой период времени и прогнозировать надежность системы в перспективе. Рассмотрена математическая модель переходных состояний системы, построенная с использованием теории марковских процессов, позволяющая рассчитать показатели надежности системы в процессе эксплуатации. В статье показано, что использование элементов теории массового обслуживания вполне адекватно описывает работу таких сложных систем, которыми являются шахтные конвейеры.

Статья в формате PDF

1467 KB

конвейерная система

эксплуатационный закон распределения

вероятность

надежность

формулы Эрланга

восстановления отказов

интенсивность отказов

интенсивность восстановления

1.Кофман А., Крюон Р. Массовое обслуживание. Теория и приложения. – М.: Изд-во «Мир», 1965. – 284 с.

2.Севастьянов Б.А. Эргодическая теория для марковских процессов и ее приложение к телефонным системам с отказами. Сб «Теория вероятностей и ее приложения». – 1957. – т. 2, вып. 1 – C. 106–116.

3.Хачатрян С.А. Проблемы надежности конвейерного транспорта угольных шахт. – Санкт-Петербург, 2004. – 181 с.

Проблема надежности стоит в центре современной техники, а исследование природы надежности на разных уровнях ее конкретизации делает практически необходимой и теоретически значимой разработку стратегии совершенствования современного и создания перспективного горнотранспортного оборудования.

Ненадежность систем и технических устройств приводит к большим экономическим потерям, повышенной трудоемкости и опасности для обслуживающего персонала.

С увеличением времени эксплуатации конвейерной линии ее надежность снижается в сравнении с проектной вследствие амортизации узлов и деталей конвейера.

По мере расходования ресурса растет число отказов, возрастают расходы на восстановление работоспособности, увеличиваются простои конвейерных линий.

Поэтому, создание математической модели надежности конвейерных систем является актуальным вопросом.

Цель исследования. Использование элементов теории массового обслуживания при решении задач надежности транспортных систем.

В теории надежности процессы возникновения отказов, проведения ремонта элементов производственных систем описывают методами теории массового обслуживания [1].

В этом случае работа любой системы массового обслуживания представляется в виде системы, на вход которой поступает в общем случае случайный поток требований с заданной интенсивностью λ(t). В зависимости от показателя обслуживания (восстановления) системы μ(t) и характера потока требований система с некоторыми вероятностями Р₀(t), Р₁(t), …, Р_n(t) может находиться в различных n (n = 0,1,2,…) возможных состояниях в любой момент времени t, т.е. число состояний системы конечно. Сами вероятности Р₁(t) количественно характеризуют качество или эффективность «обслуживания» технических систем, в том числе конвейерных линий. Следовательно, процесс функционирования системы массового обслуживания представляет собой случайный процесс дискретного типа.

Совокупность всех вероятностей Р_i(t) (i = 0,1,…,n) характеризует распределение дискретной случайной величины Х(t), принимающий значения Х₀, Х₁,…, Х_n в заданный момент времени t, поэтому справедливо равенство вида

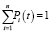, (1)

Если известно, что в начальный момент времени t = t₀ система находилась в состоянии i (P_i(t) = 1, P _j≠i(t) = 0, j = 0,1,…, i-1, i,…n), то за любой промежуток времени (t₀, t₀ + t₁) ожидается новое распределение вероятностей Р₁(t = t₁),а в момент времени t = t₂ – распределение вероятностей Р_i(t = t₂) и так далее с вероятностями перехода в эти состояния, равными Р_ik(t₀, t₁ + t₂), k = 0,1,…,i,…,n.

Все динамические системы, к которым относятся и конвейерные системы шахт, являются системами без последствия, так как большинство показателей их надежности описывается экспоненциональным законом распределения.

Важно определить вероятность перехода системы из одного (исправного) состояния в другое (неисправное) и, наоборот:

Рk(t + t) = 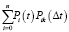. (2)

В уравнении (2) величины P_ik(Δt) есть условные вероятности того, что за время Δt техническая система (конвейер) перейдет от i приводов, находящихся в ремонте, к числу k, или тоже самое, вероятность перехода обслуживающей системы от i неработающих приводов к числу неработающих приводов k. Положим k = 0 и определим P₀₀(t) – вероятность того, что в технической системе (конвейере) через время (Δt) не будет ни одного вызова на ремонт привода при условии, что в начальный момент все приводы были в рабочем состоянии. В этом случае за время (Δt) не поступает ни одного вызова на ремонт, т.е. все привода конвейера будут в рабочем состоянии, и вероятность этого случая равна

1-w(Δt) = 1-λΔt + 0(Δt)

Но также возможен случай, что за время Δt наступит один вызов на ремонт, который будет обслужен и покинет обслуживающую систему конвейера. Тогда по истечении времени Δt все обслуживающие привода конвейера также будут в рабочем состоянии. Вероятность того, что данный вызов будет обслужен за время, не превосходящее Δt, равна

P(Δt) = 1-e ^–μΔt ≅ μ_Δt +  0(Δt)

Таким образом, вероятность того, что за время (Δt) вызов на ремонт привода поступит и будет обслужен, не превосходит величины

w(Δt)P(Δt)=[λ(Δt) + 0(Δt)][μ_Δt + 0(Δt)] = λμ(Δt)² + 0(Δt),

т.е. более высокого порядка малости, чем Δt. Вероятность же того, что за время Δt поступят и будут обслужены два и более вызовов, еще меньше. Следовательно, по теории сложения вероятностей несовместных событий имеем

P₀₀(Δt) = 1 – λΔt + 0(Δt).

Затем найдем значение вероятности Р_kk(Δt). Учитывая, что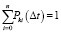, означающее что случайные события перехода конвейерной системы из состояния k неработающих приводов к состоянию i неработающих приводов (i = 0,1,…,k-1, k + 1,…,n) с учетом события: за время Δt система остается в прежнем состоянии, образуют полную группу событий. Тогда получим

P_kk(Δt)=1-P_k0(Δt)-P_k1(Δt)-…- P_kn(Δt). (3)

Очевидно, что все члены в правой части равенства (3) , кроме P_k(k-1) (Δt) и P_k(k+1) (Δt), есть бесконечно малые величины более высокого порядка малости, чем Δt. Т.к. P_ki(Δt) при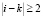 есть вероятность того, что за время Δt в обслуживающую систему поступят не менее двух вызовов на ремонт приводов (при i-k ≥2), а вероятность этого события равна

ψ(Δt) = 0(Δt) (Δt → 0),

т.е. за тоже время Δt обслуживающую систему покинут не менее двух восстановленных приводов (при k-i ≥2). Вероятность этого события равна

[P(Δt)]^k-i = [1 – e ^–μΔt]^k-i = [μΔt + 0(Δt)]^k-i = 0(Δt), т.е. эта вероятность есть бесконечно малая величина более высокого порядка малости, чем Δt (при |i-k|≥2 ).

Следовательно, имеем

P_ki (Δt) = 0(Δt) (|i-k|≥2).

Тогда равенство (3) можно записать в виде

P_kk(Δt) = 1-P_k(k-1) (Δt) – P_k(k+1) (Δt) + 0(Δt). (4)

Вычислим величину P _k(k-1) (Δt) – вероятность того, что за промежуток времени Δt из k ремонтируемых приводов освободится, по крайней мере, один из них. Вероятность того, что за время Δt привод не восстановится равна вероятности того, что время ремонта превысит Δt, т.е.

1-P(Δt) = e^–μΔt

С учетом того, что приводов конвейера равно k, то вероятность того, что не будет отремонтирован ни один из них, определяются по теореме умножения вероятностей для независимых событий и равна

(e^–μΔt)^k = e ^–kμΔt

Следовательно, используя вероятность того, что за время Δt будет отремонтирован хотя бы один из приводов, равна

1 – e^–kμΔt= kμΔt + 0(Δt) (Δt → 0).

Учитывая, что вероятность ремонта двух и более приводов за время Δt имеет малости 0(Δt), то вероятность того, что за время Δt будет восстановлен точно один привод из k, равна

P_k(k-1) (Δt) = kμΔt + 0(Δt) (0 ≤k ≤n).

Заметим, что вероятность начала и окончания ремонта одного и того же числа отказавших объектов за время Δt также имеет порядок малости Δt.

Необходимая вероятность P_k(k-1) (Δt) с точностью до Δt равна

P_k(k+1) (Δt) = λΔt + 0 (Δt)  (0 ≤ k ≤ n –1).

С учетом полученных выражений для P_k(k-1) (Δt) и P_k(k+1) (Δt) равернство (4) примет вид

P_kk (Δt) = 1 – λΔt – kμΔt + 0(Δt)   (0 ≤ k ≤ n –1).

Аналогично из формулы (4) получим величину P_nn (Δt) при условии, что P_n(n+1) (Δt) = 0 (переход от n ремонтируемых приводов к n + 1 восстанавливаемому приводу невозможно, т.к. их всего n по условию постановки задачи). Отсюда получим

P_nn (Δt) = 1 – nμΔt + 0(Δt)

Подставляя полученные выражения в (2) при k = 0, 1 ≤ k ≤ n –1 и k = n, получим следующую группу уравнений:

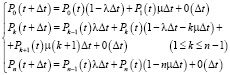(5)

После некоторых преобразований (перенос в первом уравнении P₀(t), во втором P_k(t), а в третьем P_n(t); деление обеих частей всех уравнений на Δt) и переходе к пределу при Δt → 0 окончательно получим

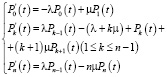(6)

Неизвестные функции P_k(t) (k = 0,1,…,n), зависящие от параметров λ и μ, содержат произвольную постоянную, которая определяется из условия нормировки

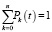, (7)

Так как нет необходимости иметь точные решения системы (6), то решение последней получают из системы вида

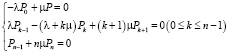(8)

Система (8) получена из системы (6) на основе теоремы Маркова (существование пределов 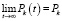(0 ≤ k ≤ n) и равенства нулю предела при t → ∞ левых частей системы (6) и являются системой линейных однородных алгебраических уравнений относительно неизвестных P₀, P₁,…,P_n.

Решение системы (8) имеет вид

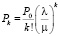(k = 1,2,…,n) (9)

где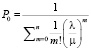 , (10)

Таким образом, формулы (9) и (10), называемые формулами Эрланга определяют решение поставленной задачи (в предельном случае при t → ∞ ).

На основе их можно вычислить основной критерий функционирования конвейерной системы вероятности ее отказа. Т.к. очередное требование на ремонт не будет принято на обслуживание только в том случае, когда все привода будут находиться в ремонте, т.е. если k = n. Поэтому, вероятность отказа всей конвейерной системы равна

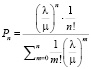(11)

C введением величин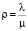 приведенной плотности потока вызовов на ремонт приводов (коэффициент неисправностей обслуживаемой конвейерной системы) формулы (9)-(11) примут вид

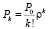(k = 1,2,…,n);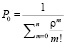 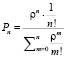 . (12)

С учетом полученных формул можно определить математическое ожидание числа приводов, находящихся в ремонте

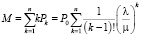. (13)

Заметим, что несмотря на то, что только при допущении о показательном распределении времени ремонта приводов конвейерной системы, процесс становится процессом Маркова и для этого случая получены формулы (9)-(11), тем не менее эти формулы имеют гораздо более широкое применение. В работах Севастьянова Б.А. показано, что эти формулы справедливы также и при произвольном законе распределения времени ремонта (восстановления) объектов сложных технических систем, к которым относятся конвейерные линии угольных шахт [2]

Библиографическая ссылка