Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Суздалевич В.А. 1

---

1 ФГБОУ ВПО «Московский Государственный Технический Университет им. Н.Э. Баумана»

Экспериментально исследовано влияние электронного облучения на коэффициент пропускания оптического стекла КУ-1. Показано, что основные изменения этого параметра происходят в коротковолновой области исследованного диапазона от 200 до 2500 нм. Оптические характеристики образцов как исходных, так и облученных стекол были измерены с помощью спектрофотометра и многоцелевой приставки RTA-2000 с интегрирующей сферой спектрофотометра MPS-2000 фирмы «Шимадзу». До и после облучения поверхности образцов были исследованы с помощью атомно-силового микроскопа (АСМ) Solver P47 – Multi – Technique SPM. Для анализа экспериментальных данных предложена модель, описывающая накопление радиационно-стимулированных центров окраски. В результате анализа полученных данных установлено, что увеличение оптической плотности стекла можно объяснить генерацией в стекле центров окраски и его деструкцией при электростатических разрядах, сопровождающих облучение.

Статья в формате PDF

2070 KB

центры окраски

электронное облучение

коэффициент пропускания

оптическая плотность

электростатический разряд

1. Арбузов В.И., Толстой М.Н., Элертс М.А. Абсолютные характеристики центров окраски в стекле Na2O*3SiO2 // Изв. АН СССР. Серия физическая. – 1986. – Т. 50, № 3. – С. 126-131.

2. Глебов Л.Б., Докучаев В.Г., Петровский Г.Т. Исследования спектров поглощения ?-окрашенных силикатных стекол высокой частоты с переменным содержанием Fe3+ // Физика и химия стекла. – 1985. – Т. 11, № 1. – С. 79-96.

3. Глебов Л.Б., Докучаев В.Г., Петров М.А., Петровский Г.Т. Спектры поглощения центров окраски щелочносиликатных стеклах // Физика и химия стекла. – 1990. – Т. 16, № 1. – С. 39-47.

4. Сергеев П.М., Ермоленко Т.А., Евлампиев И.К., Зворыкин В.Д., Попов С.А., Пронина М.С., Сергеев А.П., Туроверов П.К., Черемисин И.И. Наведенное электронным пучком поглощение в кварцевых стеклах // Оптический журнал. – 2004. – В.71, № 6. – С.93-97.

5. Сергеев А.П., Сергеев П.Б. Зависимости интенсивности полос поглощения в высокочистых кварцевых стеклах от флюенса электронного пучка // Оптический журнал. – 2011. – Т. 78, № 5. – С.77-83.

6. Суздалевич В.А., Хасаншин Р.Х. Элементарная модель накопления центров окраски при электронном облучении стекла К-208 // Труды XV межвузовской научной школы молодых специалистов «концентрированные потоки энергии в космической технике, электронике, экологии и медицине» (Москва, 25-26 ноября 2014 г.). – Москва, 2014. – С. 152-155.

7. Хасаншин Р.Х., Тимофеев А.Н., Просвириков В.М., Першина Е.О. Радиационно-стимулированные изменения оптических свойств модельных композиционных материалов // Вопросы атомной науки и техники. Сер.: Физика радиационного воздействия на радиоэлектронную аппаратуру. – 2008. – Вып. 1 – С. 14-17.

8. Хасаншин Р.Х., Новиков Л.С. Изменения спектра пропускания стекла марки К-208 под действием ионизирующих излучений и молекулярных потоков // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. – 2014. – № 7. – С. 83-87.

9. Хасаншин Р.Х., Надирадзе А.Б. Изменение оптических свойств функциональных поверхностей космических аппаратов при совместном воздействии электронов и ультрафиолета // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. – 2013. – № 3. – С. 73-78.

10. Khasanshin R.H., Novikov L.S. Structural changes of surfaces of spacecraft solar array protective glasses being irradiated by 20-keV electrons // Advances in Space Research. 2016. V. 57. Iss.10. P. 2187-2195.

Исследования радиационного воздействия на оптические материалы представляет актуальную проблему как с позиции фундаментальных проблем физики и химии твердого тела, так и при решении многих задач современного материаловедения. В частности, в связи с оснащением современных космических аппаратов (КА) высокоточным оптическим оборудованием, проблема радиационной стойкости оптических материалов становится одной из определяющих в космической отрасли. Например, на геостационарной орбите материалы внешних поверхностей спутников подвергаются дозовым нагрузкам порядка 8,8106 Гр/год.

Деградация оптических свойств функциональных поверхностей КА, как правило, обусловлена осаждением на них продуктов собственной внешней атмосферы и действием ионизирующих излучений космического пространства. Такие изменения ведут к увеличению коэффициента поглощения солнечной энергии терморегулирующих покрытий [7] и к уменьшению коэффициента пропускания защитных покрытий солнечных батарей [8, 9]. В результате этих изменений нормальная работа жизненно важных систем КА нарушается.

Ионизирующие излучения генерируют в стекле свободные электроны и дырки, локализация которых на соответствующих ловушках приводит к появлению электронных и дырочных центров окраски. При этом они отличаются положением, полушириной и амплитудой полос поглощения, а суммарный их спектр перекрывает диапазон от ультрафиолета до инфракрасной области. Исследованию образования центров окраски в стекле при облучении -квантами и электронами с энергией более 100 кэВ посвящено большое количество работ, например [1-4]. Однако причины деградации оптических свойств стекол под действием ионизирующих излучений средних энергий (550 кэВ), характерных для частиц горячей магнитосферной плазмы, изучены недостаточно.

Данная работа посвящена анализу спектров пропускания образцов оптического кварцевого стекла КУ-1, облученных разными флюенсами электронов с энергией 40 кэВ и построению физико-математической модели, аппроксимирующей полученные экспериментальные данные.

Модель накопления центров окраски

При математическом описании динамики накопления радиационно-стимулированных дефектов в материале, при воздействии на него излучений космического пространства должно учитываться как распределение дозовых нагрузок по глубине материала, так и изменение спектрального состава излучений. Поэтому в модели предполагается, что концентрация дефектов – центров поглощения материала должна зависеть как от времени, так и пространственной координаты (в нашем случае можно рассматривать одномерную задачу). Поэтому изменение концентрации дефектов можно описать с помощью следующего линейного дифференциального уравнения:

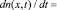
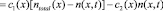(1)

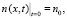(2)

где n0 – начальная концентрация центров поглощения;

ntotal – полное количество центров поглощения в материале, которое приходится на единицу площади (на 1 см2), очень тонкого слоя материала при этом n0 < ntotal;

c1(x) и c2(x) – вероятности образования и разрушения центров поглощения в единицу времени. При этом c1(x) = K•S(x), где S(x) – функция источника. Вид функции источника по форме приблизительно повторяет распределение поглощенной дозы излучения в стекле, которое рассчитывается методом Монте-Карло. Для моноэнергетических электронов перпендикулярно направленных к поверхности плоской мишени функцию источника можно аппроксимировать следующим выражением:

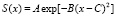(3)

где А, В и С – параметры, значения которых зависят от начальной энергии (Ео) и плотности потока электронов, а также от состава и толщины мишени. В качестве примера на рис. 1 приведены функции источника для трех значений энергии электронов, взаимодействующих со стеклом.

Подробные тестовые расчеты по описанной модели (1)-(2) приведены в работе [6].

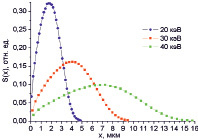
Рис. 1. Функции источника для разных энергий электронов

Связь интенсивности прошедшего света от времени и концентрации наведенных центров окраски зададим законом Бугера, который для нашей модели будет иметь следующий вид:

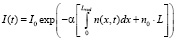(4)

где 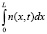– наработанные центры окраски; Lrad – длина свободного пробега электронов, Lrad = 16 мкм; n0 – начальная концентрация центров окраски в необлученном образце по толщине материала, L – общая толщина образца.

Разберем методику расчёта изменения оптической плотности при облучении разными флюенсами электронов.

Интенсивность света, прошедшего необлученное стекло:

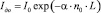(5)

где I0 и Iдо – начальная интенсивность света и интенсивность света, прошедшего необлученное стекло соответственно.

Интенсивность света, прошедшего облученное стекло:

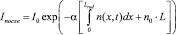(6)

где Iпосле – интенсивность света, прошедшего облученное стекло.

Т.к. коэффициент пропускания по определению: T = I/I0 и используя формулы (5) и (6) получаем:

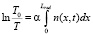(7)

где T0 – коэффициент пропускания необлученного образца стекла.

Окончательно получаем формулу для вычисления изменения оптической плотности стекла после облучения следующего вида:

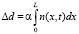(8)

Как видно из формулы (8), изменение оптической плотности пропорционально концентрации центров окраски.

Материалы и методы исследования

Для проведения экспериментов были изготовлены образцы размером 40402 мм из кварцевого стекла марки КУ-1. Перед облучением поверхности образцов очищались дистиллированной водой в ультразвуковой ванне и далее сушили при температуре 100 °С.

Облучения образцов, прикрепленных к охлаждаемому заземленному металлическому столику моделирующей установки УВ- (ОАО «Композит») [10], проводилось в вакуумной камере при давлении 10-4 Па. Энергия электронов составляла 40 кэВ, а флюенсы облучения варьировались в диапазоне Фe = 101521016 см-2. Оптические характеристики образцов как исходных, так и облученных стекол измеряли с помощью спектрофотометра и многоцелевой приставки RTA-2000 с интегрирующей сферой спектрофотометра MPS-2000 фирмы «Шимадзу». Измерения проводились в спектральном диапазоне (2002500 нм) с разрешением 2 нм. Зондирующее излучение направлялось перпендикулярно к поверхности подложки, размер его пятна на поверхности составлял около 35 мм. Фотометрическая погрешность измерений не превышала 0.3 %.

До и после облучения поверхности образцов исследовались с помощью атомно-силового микроскопа (АСМ) Solver P47 – Multi – Technique SPM. Для изучения топологии поверхности образцов использовалась полуконтактная атомно-силовая мода, которая при высокой точности измерений не разрушает поверхность.

Результаты исследования и их обсуждение

Результаты измерений спектрального коэффициента пропускания стекла исходного и облученного до разных значений флюенсов представлены на рис. 2.

Для спектрального коэффициента пропускания видны следующие особенности: увеличение флюенса приводит к снижению коэффициента пропускания, при этом коротковолновая и длинноволновая области спектра имеют различную кинетику.

На рис. 3 представлено изменение оптической плотности от длины волны для разных значений флюенсов облучения. Видно, что в коротковолновой области происходит максимальное увеличение оптической плотности. Это согласуется с данными, представленными в работах [5], где отмечается, что в спектре пропускания образцов стекла КУ-1, облученных электронами с энергией 280 кэВ в области 160-260 нм имеется шесть индивидуальных полос поглощения.

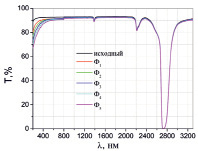
Рис. 2. Спектральный коэффициент пропускания КУ-1 для следующих значений флюенса: Ф1 = 4.111019 1/м2, Ф2 = 1.2410201/м2, Ф3 = 2.0610201/м2, Ф4 = 2. 9010201/м2, Ф5 = 4.2010201/м2

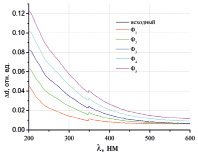
Рис. 3. Зависимость приращения оптической плотности от длины волны для разных флюенсов

На рис. 4 представлена экспериментальная зависимость изменения оптической плотности от флюенса на разных длинах волн. Видно, что на длине волны = 213 нм происходит более сильное изменение оптической плотности.

На рис. 5 приводятся кривые, аппроксимирующие экспериментальные данные с указанием значений параметров для выражения (9). При этом экспериментальная зависимость оптической плотности от флюенса облучения представлена в виде суммы двух функций: первая (d1) выходит на насыщение и хорошо согласуется с моделью накопления центров окраски, вторая (d2) имеет квазилинейный характер. Можно предположить, что квазилинейный процесс увеличения оптической плотности облученных образцов связан с деструкцией стекла и нарушением стехиометрии стекла при электростатических разрядах [10].

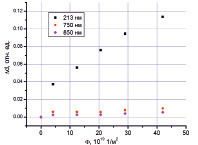
Рис. 4. Зависимость приращения оптической плотности от флюенса для разных длин волн

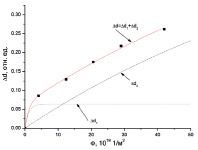
Рис. 5. Экспериментальная зависимость приращения оптической плотности стекла от флюенса и ее аппроксимация двумя составляющими

Для зависимостей, представленных на рис. 5, получены конкретные значения параметров и аппроксимирующие функции, которые имеют следующий вид:

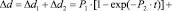
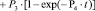(9)

где P1 = 0.0638 ± 0.0003; P2 = 8.760110-20 ± ± 5.316910-20 м2; P3 = 0.5878 ± 0.0002; P4 = 1.001710-21 ± 1.584610-23 м2.

Заключение

При исследовании влияния электронного облучения с энергией частиц 40 кэВ образцов оптического стекла КУ-1 получены следующие результаты:

1. По мере роста дозы облучения спектральный коэффициент пропускания снижается во всем исследованном диапазоне. Максимальное уменьшение этого параметра наблюдается в коротковолновом диапазоне длин волн.

2 Для аппроксимации экспериментальных данных предложена модель накопления индуцированных излучением центров окраски.

3. Экспериментальная зависимость изменения оптической плотности стекла от флюенса облучения представлена в виде двух составляющих. Первая удовлетворительно описывается в рамках предложенной модели и с увеличением флюенса выходит на насыщение, а вторая имеет квазилинейный характер и ее существование предположительно связано с деструкцией и нарушением стехиометрии стекла при электростатических разрядах, сопровождающих его облучение.

Библиографическая ссылка