В стратегии развития Российского государства в качестве одного из приоритетов определена национальная безопасность, одним из важнейших элементов последней является информационная безопасность. Именно поэтому разработка безопасных и эффективных информационных систем является одним из приоритетных направлений развития РФ. Решая задачи создания новых технологий информационной безопасности необходимо, сочетать с одной стороны высокую скорость обработки и передачи больших объемов информации, а с другой – ограничения доступа к ней, обеспечивая требуемый уровень защиты информации.
Цель исследования
Одним из наиболее перспективных направлений развития информационных технологий является широкое проникновение систем электронных платежей (СЭП) практически во все сферы деятельности современного государства. Однако при этом использование таких информационных технологий непосредственно связано с определенной совокупностью рисков, основой причиной которых являются уязвимости информационных технологий и систем.
В настоящее время для эффективной работы автономной системы электронных денег предлагается использовать ряд криптографических протоколов. Математическую основу большинства этих протоколов составляют, так называемые, алгоритмы доказательства с нулевым разглашением. В данных протоколах довольно часто применяют псевдослучайные функции (ПСФ). Кроме этого ПСФ нашли широкое применение в самых различных сферах. В работах [1-4] рассмотрены вопросы применения псевдослучайных функций в космических технологиях. В работах [5, 6] довольно подробно рассмотрены вопросы применения псевдослучайных функций повышенной эффективности для реализации протоколов «снятие со счета», «выплаты одной монеты» и «определение двойной выплаты».
Применение псевдослучайных функций позволяет разрабатывать процедуры защиты информации, обладающие всеми достоинствами систем нелинейного криптографии, обеспечивающие реальный масштаб времени закрытия информации. При этом в основу построения таких ПСФ положены операции, связанные с процедурами сложения, умножения, возведения в степень элементов полей Галуа, а также их различных комбинаций. Очевидно, что это способствует существенному повышению уровня обеспечения конфиденциальности и целостности информации [7].
Так как каждая область применения выдвигает свои требования к свойствам псевдослучайной функции, то разработка генератора, позволяющего реализовать ПСФ требуемого качества, является актуальной задачей. Поэтому целью исследований является разработка структуры генератора псевдослучайной функции, позволяющего при меньших схемных затратах обеспечить требуемый уровень защиты информации от несанкционированного доступа.
Материалы и методы исследования
Для разработки схемной реализации генератора ПСФ повышенной эффективности рассмотрим алгоритм вычисления псевдослучайной функции Naor-Reingold, которая в качестве аргументов использует ключ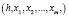 
и входные данные в двоичном коде 
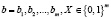. В этом случае значение выходного вектора генерирующего устройства будет определяться
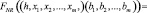
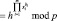, (1)
где h – первообразной элемент мультипликативной группы, порожденный простым числом p; m – разность двоичный кода.
С целью сокращения времени вычисления значений псевдослучайной функции в работах [8, 9] был предложен алгоритм получения ПСФ, обладающей повышенной эффективностью. При этом вычисление выходного отклика определяется
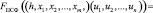
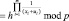(2)
где U = u1, u2,…, un – входной код; X = x1, x2,…, xm – секретный ключ; m – разрядность двоичного кода;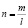 
количество блоков; l – разрядность блока.
Очевидно, что применение алгоритма (2) позволяет сократить время вычисления ПСФ в l раз, по сравнению с классической реализацией псевдослучайной функции согласно равенства (1).
На рисунке представлена схема разрабатываемого генератора псевдослучайной функции повышенной эффективности. Он содержит первый вход и второй вход, которые предназначены для подачи в генератор секретного ключа х и входного кода u. Для хранения этих значений используются первый регистр и второй регистр. Для получения значения ПСФ используется сумматор по модулю p. Чтобы определить мультипликативно обратный элемент в состав генератора введен блок вычисления обратного элемента (ВОЭ) по модулю p. Кроме того генератор ПСФ содержит умножитель по модулю p, третий регистр, блок возведения в степень по модулю p. Выход последнего является выходом устройства.
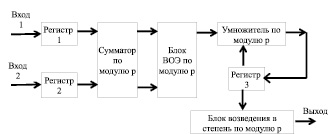
Схемная реализация генератора ПСФ
Результаты исследования и их обсуждение
Рассмотрим пример работы разработанного генератора псевдослучайной функции повышенной эффективности. Пусть модуль p = 11. В качестве первообразного элемента выбираем h = 2. Предположим, что в качестве секретного ключа выбирается число X = 810, которое принадлежит мультипликативной группе модуля р = 11. В качестве входного значения, поступившего в генератор ПСФ, выбираем число U = 1010. Представим эти значения в двоичном коде. В результате преобразований имеем следующие значения
U = 1010 = 10102; X = 810 = 10002.
Полученные значения, представленные 4 битовым блоком, разобьем эти на 2 блока, по 2 бит каждый. В результате этого имеем
u1 = 102 = 210; u2 = 102 = 210; x1 = 102 = 210; x2 = 002 = 010.
Для вычисления ПСФ повышенной эффективности используем выражение (2).
В этом случае
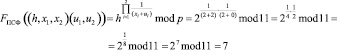
Рассмотрим работу устройства. Перед началом работы генератора в третий регистр записывается единица. На первый вход подается в двоичном коде первый блок секретного ключа х1 = 102, который записывается в первый регистр. На второй вход поступает первый блок входного кода u1 = 102, который записывается в о второй регистр. С выходов первого и второго регистров значения х1 и u1 поступают на входы сумматора по модулю p = 11, на входе которого появляется результат
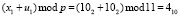
Данное значение с выхода сумматора подается на вход блока вычисления обратного элемента по модулю p = 11. Работа этого блока представлена в таблице.
Обратные элементы по модулю p = 11
|
Элемент a |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Обратный элемент a-1 по модулю p = 11 |
1 |
6 |
4 |
3 |
9 |
2 |
8 |
7 |
5 |
10 |
С выхода блока вычисления обратного элемента по модулю p = 11 снимается значение 3, которое поступает на первый вход умножителя по модулю p = 11 на второй вход которого поступает 1 с первого выхода третьего регистра. Умножитель по модулю выполняет операцию, и в третий регистр записывается число 3.
Затем на первый и второй входы и соответственно подаются вторые блоки секретного ключа х2 = 002 = 010 и входных данных u2 = 102 = 210. Данные значения записываются в первый и второй регистры соответственно. С входа регистров данные блоки поступают на входы сумматора по модулю 11, где реализуется процедура
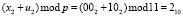
Вычисленное значение подается на вход блока вычисления обратного элемента по модулю p = 11. Согласно данным, приведенным в таблице, с выхода блока ВОЭ будет снято число 6, которое поступит на первый вход умножителя по модулю p = 11. На второй вход подается число 3 с первого выхода третьего регистра, который используется в качестве хранилища промежуточных результатов. На выходе умножителя 7 по модулю p = 11 появляется результат
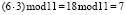
Вычисленное значение поступает в третий регистр. Так как вычисления закончены, то это значение со второго выхода регистра подается на вход блока возведения в степень по модулю p = 11,который реализует процедуру (2). В результате имеем
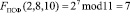
Проведем сравнительную оценку времени вычисления ПСФ согласно алгоритма, задаваемого выражением (1) и алгоритма (2). Анализ этих выражений показывает, что основным фактором, от которого будет зависеть время характеристики генератора ПСФ будет вычисления показателя степени. Из выражения (1) наглядно видно, чтобы реализовать эту процедуру необходимо выполнить (m-1) умножений данных размером [log2 p].
При использовании выражения (2) число таких умножений сокращается в l раз, где –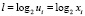 
– разность блоков.
Таким образом, очевидно, что применение выражения (2) позволяет повысить быстродействие генератора псевдослучайной функции повышенной эффективности в l раз по сравнению с вычислением ПСФ согласно равенства (1).
Заключение
В статье рассмотрена структура генератора псевдослучайной функции, которая позволяет обеспечить требуемый уровень защиты информации от несанкционированного доступа при меньшей длине ключа. Проведенная сравнительная оценка времени реализации псевдослучайных функций показал, что разработанный генератор позволяет реализовать каскадную ПСФ, которая в отличии от псевдослучайной функции Naor-Reingold сокращает число умножений. Это позволило разработать генератор ПСФ на реализацию которого потребуется меньше схемных затрат.</p
Библиографическая ссылка
Писковацкий Н.Е., Филатов А.Д., Калмыков И.А., Ряднов С.А. РАЗРАБОТКА СТРУКТУРЫ ГЕНЕРАТОРА МОДУЛЯРНОЙ ПСЕВДОСЛУЧАЙНОЙ ФУНКЦИИ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 7-2. – С. 151-154;URL: https://applied-research.ru/ru/article/view?id=9783 (дата обращения: 21.11.2024).