Современные космические аппараты (КА) оснащены большим количеством высокочувствительной аппаратуры, нормальное функционирование которой может быть нарушено вследствие неучтенного воздействия собственной внешней атмосферы (СВА). СВА – это газовое облако, образующейся в окрестности КА за счет потери массы материалов поверхности, газовыделения негерметичных отсеков, работы электроракетных двигателе и т.д. [1, 2]. Осаждение частиц СВА на чувствительных к загрязнениям поверхностях приводит к множеству негативных последствий, например, таких как снижение светопропускания и появление ложных срабатываний оптических приборов [3- 5]. Острота этой проблемы обусловлена широким применением полимерных композиционных материалов (ПКМ), в качестве терморегулирующих покрытий КА, которые являются основными источниками летучих веществ (ЛВ), создающими предпосылки для увеличения плотности СВА и присутствия в ее составе высокомолекулярных легкоконденсирующихся соединений.
В связи с тенденцией к увеличению сроков активного существования изделий космической техники, предъявляются повышенные требования к надежности прогнозирования уровней загрязнения функциональных поверхностей КА в условиях эксплуатации. Применение содержательных физико-математических моделей для описания источников летучих веществ в задачах расчета СВА КА ограничивается сложностью определения коэффициентов дифференциальных уравнений моделей из экспериментальных результатов. Поэтому разработка алгоритмов для их оценки является актуальной задачей.
Методика и результаты эксперимента
В качестве модельного материала для экспериментального исследования был выбран ЭКОМ-1 – штатное терморегулирующее покрытие КА. Из этого материала, нанесенного толщиной 100 мкм на подложку из Амг-6, были изготовлены образцы, которые взвешивали до и после тепло-вакуумного воздействия при давлении 10-4 Па. Для исследования динамики потери массы материалов использовались кварцевые микровесы – измерительное устройство, предназначенное для преобразования изменения массы, присоединенной к поверхности кварцевого пьезорезонатора, в приращение выходной частоты автогенератора.
Масс-спектры зарегистрированные в диапазоне величин m/z от 25 до 700 на приборе МАТ-900 фирмы Термо-Финниган методом прямого ввода образца ЭКОМ-1 при температуре 120оС в ионный источник показали, что тепло-вакуумное воздействие на материала приводит к выходу ЛВ, имеющих сложный молекулярный состав (рис. 1).
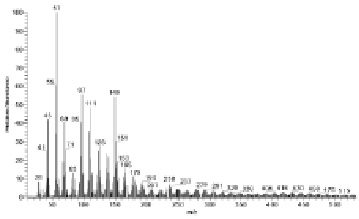
Рис. 1. Масс-спектр образца ЭКОМ-1 при температуре 120 °С
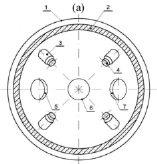
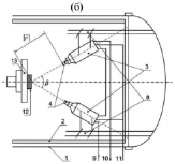
Рис. 2. Схема расположения ДПМ в вакуумной камере. 1 – внешняя стенка вакуумной камеры; 2 – цилиндрическая полость, заполняемая жидким азотом; 3 – термостаты; 4 – датчики потери массы; 5 (7) – входное окно ускорителя электронов (протонов); 6 – входное окно имитатора концентрированного солнечного излучения; 8 – система позиционирования термостатов с датчиками ПМ; 9, 10 – ввод и вывод теплоносителя; 11 – кабель питания и измерений; 12 – образец материала; 13 – изотермическая ячейка
Поэтому для получения подробной информации о зависимости потери массы образцов использовалась система из четырёх кварцевых микровесов – датчиков потери массы (ДПМ), термостатированных при разных температурах (293, 233, 203, 78К) [6]. Схема расположения датчиков в вакуумной камере изображена на рис. 2.
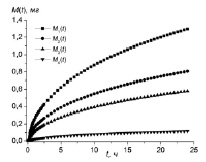
Рис. 3. Зависимости потери массы образца ЭКОМ-1 за счет разных групп молекул осевших на ДПМ, термостатированных при разных температурах: M1(t) – 293 °K; M2(t) – 233 °K; M3(t) – 203 °K; M4(t) – 78 °К
Каждый ДПМ с чувствительностью (4.7 ± 0.1)10-9 г/(Гц•см2), состоит из двух 10-МГц кварцевых резонаторов AT-среза марки РК 171, включенных в цепь отдельных генераторов. Один из кварцевых резонаторов служит опорным, он изолирован от попадания ЛВ, а второй рабочий, его поверхность открыта. Наличие в системе четырёх датчиков, термостатированных при разных значениях температуры, позволяет в каждом эксперименте разделить ЛВ, выделяющиеся из материала, условно на четыре группы:
– «тяжёлые легко конденсирующиеся» осаждаются на чувствительных элементах всех датчиков № 1№ 4 (при 87 Т 293 К);
– «тяжёлые» осаждаются на датчиках № 1, № 2 и № 3 (при 87 Т 233 К);
– «средние» осаждаются на датчиках № 1 и № 2 (при 87 Т 203 К);
– «лёгкие» осаждаются только на датчике № 1 (при Т = 87 К);
При этом массы «лёгких», «средних» и »тяжёлых» ЛВ определяются из выражений:
М1(t) – М2(t); М2(t) – М3(t); М3(t) – М4(t), соответственно, где Мi(t) – масса ЛВ, накопленных на i-ом датчике; М4(t) – масса «тяжёлых легко конденсирующихся» ЛВ.
В качестве примера на рис. 3 представлены экспериментальные результаты, полученные при помощи описанной выше системы из четырех ДПМ.
Математическая модель потери массы ПКМ в вакууме и алгоритм оценки ее параметров.
Изменение концентрации ЛВ в материале при вакуумно-тепловом воздействии обусловлено диффузией и десорбцией ЛВ с поверхности материал-вакуум. Толщина образцов материала 103 раза меньше остальных линейных размеров, следовательно, можно пренебречь краевыми эффектами и рассматривать одномерную задачу: при этом потеря массы происходит только через свободную поверхность материал-вакуум. В рамках сделанных предположений решение задачи о потере массы ПКМ сводится к решению следующей краевой задачи [7]:
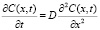, 0< x < l, t > 0 (1)
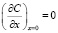, (2)
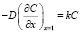(3)
C(x, 0) = C0 = const, (4)
где D – эффективный коэффициент диффузии, мкм2с-1; k – эффективный коэффициент десорбции, мкм•с-1; l – толщина образца материала, мкм; C0 – распределение концентрации ЛВ в материале в начальный момент времени, молекул•мкм-3.
Решением системы (1)-(4) является пространственно-временное распределение ЛВ в образце модельного материала:
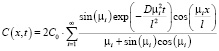, (5)
где µi – корни следующего трансцендентного уравнения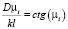 
.
В рамках принятой модели (1)-(4) зависимость массы образца от времени имеет вид:
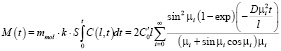, (6)
где mmol – масса молекул, S – площадь поверхности образца,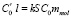 
.
Из формулы (6) видно, что решением задачи (1)-(4) является бесконечный ряд. Так как нас интересует закономерность процесса потери массы на достаточно длительном интервале времени, то для его приемлемого описания достаточно ограничиться несколькими первыми членами ряда. При исследовании ряда (6) выявлено, что добавление к сумме первых четырех-пяти слагаемых, последующих членов ряда, не приводит к значительному повышению точности.
В данной работе для построения модели мы использовали пять слагаемых ряда в формуле (7), что достаточно для удовлетворительной оценки.
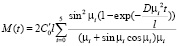. (7)
Задача, поставленная в данной работе, заключается в нахождении таких значений параметров D и k, при которых функция M(t) наилучшим образом приближает значения, полученные в ходе эксперимента. Ориентируясь на метод наименьших квадратов (МНК), мерой близости функции (7) к экспериментальным данным будем считать сумму квадратов отклонений:
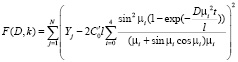(8)
где Yj – экспериментальные данные о потере массы образца ПМК в вакууме на j-й момент времени, а M(tj) – значение функции, определяемой (7) при t = tj.
Оценка значений эффективных коэффициентов диффузии и десорбции путем, минимизации F(D, k) по параметрам D и k связана с рядом проблем, обусловленных видом целевой функции (8), которые делают процесс минимизации весьма затруднительным:
1) Параметр решения задачи (1)-(4) i связан с параметрами модели D и k трансцендентным уравнением, что осложняет аналитическое вычисление производных целевой функции.
2) Наличие большого количества локальных экстремумов, в широкой окрестности которых градиент целевой функции (8) очень мал, приводит к ложному определению минимума и это обстоятельство усложняет применение для решения поставленной задачи многих традиционных методов.
Поэтому в данной работе для решения задачи минимизации целевой функции был применен алгоритм искусственной пчелиной колонии [8, 9]. В данном подходе каждое решение представляется в виде объекта (пчелы), который инициализируется своими «координатами» (некоторыми значениями искомых коэффициентов D и k) и имеет значение равное величине целевой функции рассчитанной при соответствующих параметрах.
Алгоритм искусственной пчелиной колонии можно описать следующим образом:
1. Инициализация N объектов случайными координатами из заданной области. То есть пчелы-разведчики отправляются в точки со случайными параметрами функции.
2. Вычисление значений объектов (значений целевой функции). Наименьшая полученная величина целевой функции запоминается как промежуточное решение.
3. Проверяется условие останова для промежуточного решения. В рассматриваемом случае условием останова будет достаточно малая величина невязки, т.е. функции (8). Если условие останова было достигнуто, то промежуточное решение является искомым.
4. В зависимости от значения целевой функциивыделяются два вида перспективных участков на поверхности функции, вблизи которых возможно располагается глобальный экстремум. А именно:
Выбирается n (n < N) лучших участков, где значения целевой функции меньше всех;
Выбирается m (m < n) так называемых выбранных участков, где значения целевой функции хуже, чем на лучших участках, но эти участки все равно являются неплохими с точки зрения значения целевой функции.
5. Инициализация объектов случайными координатами в окрестности выбранных участков (лучшие участки рассматриваются более подробно), а также p = N – m – n оставшихся объектов определяются случайными координатами из всей рассматриваемой области.
6. Возвращаемся к пункту 2.
Несмотря на то, что рассмотренный алгоритм требует большого количества итераций, во многих случаях он обладает рядом несомненных преимуществ при решении задачи поиска глобального экстремума. А именно:
1) В отличие от градиентных методов, он не требует вычисления производных.
2) Подходит для сложных целевых функций с наличием большого количества локальных экстремумов.
В результате обработки экспериментальных данных с использованием выбранной модели для каждой группы молекул получены оценки эффективных коэффициентов диффузии и десорбции, которые представленные в таблице, а также построены графики аппроксимирующие экспериментальные данные (рис. 4).
|
Группа молекул |
Температура |
D, см2/с |
k, см/с |
|
Легкие |
87 °K |
2.9•10-8 |
3.1•10-4 |
|
Средние |
87 °K < Т 203 °K |
1.25•10-8 |
7•10-5 |
|
Тяжелые |
203 °K < Т 233 °K |
3.7•10-8 |
3.4•10-4 |
|
Тяжёлые легко конденсирующиеся |
293 °K Т |
9.02•10-9 |
1.6•10-4 |
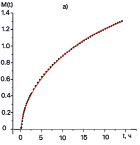
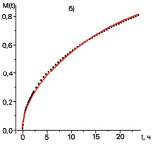
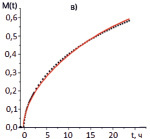
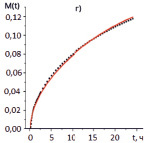
Рис. 4. Экспериментальные и теоретические зависимости потери массы образца от времени: а) легкие молекулы; б) средние молекулы; в) тяжелые молекулы; г) легко конденсирующиеся молекулы; – экспериментальные данные; – результаты аппроксимации
На рис. 4 демонстрируется сравнение результатов расчетов, проведенных с использованием полученных значений параметров математической модели потери массы, с экспериментальными данными.
Выводы
При расчетно-экспериментальных исследованиях термостимулированной потери массы полимерного композита в вакууме получены следующие результаты:
1. Проведен численный анализ экспериментальных данных о потере массы терморегулирующего покрытия космических аппаратов при вакуумно-тепловом воздействии, полученных с использованием системы состоящей из четырёх кварцевых микровесов, термостатированных при различных температурах. Анализ этих результатов и масс-спектров исследуемого материала позволил разделить совокупность молекул выделяющихся из него в вакууме на четыре группы, в соответствии с их массами. Коэффициенты уравнений модели, описывающей изучаемый процесс, напрямую зависят от эффективных масс молекул, поэтому такое разделение приводит к повышению точности оценки этих параметров.
2. Построен алгоритм для оценки значений эффективных коэффициентов диффузии и десорбции – параметров математической модели, описывающей процесс термостимулированной потери массы полимерного композита. При обработке экспериментальных результатов получены значения указанных параметров.
3. Результаты расчётов, проведенных с использованием полученных значений эффективных коэффициентов диффузии и десорбции, удовлетворительно согласуются с экспериментальными данными.
Библиографическая ссылка
Власова А.М. МОДЕЛИРОВАНИЕ ТЕРМОСТИМУЛИРОВАННОЙ ПОТЕРИ МАССЫ ПОЛИМЕРНОГО КОМПОЗИТА В ВАКУУМЕ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 7-2. – С. 169-174;URL: https://applied-research.ru/ru/article/view?id=9787 (дата обращения: 19.04.2024).