Теоретическое рассмотрение кавитации пузырьков в жидкости восходит еще ко временам Рэлея [2]. К теме пузырькового синтеза научное сообщество вернулось после публикации статьи [4]. Физические процессы, происходящие при взаимодействии пузырьков являются интересными и достойными для научных исследований сложных процессов при схлопывании отдельного пузырька [1]. Как известно, кавитационные пузырьки (КП) образуются в тех местах, где давление жидкости становится некоторого критического значения pкр (в реальной жидкости pкр приблизительно равно давлению насыщенного пара этой жидкости при данной температуре). Если понижение давления происходит вследствие больших местных скоростей в потоке движущейся капельной жидкости, то кавитация называется гидродинамической.
Для идеальной однородной жидкости вероятность образования пузырьков за счет разрыва жидкости становится заметной при больших растягивающих напряжениях так, например, теоретическая прочность на разрыв воды равна 1,5•108 Па (1500 кгс/см2) [4]. Максимальное растяжение тщательно очищенной воды, достигнутое при растяжении воды при 10 °С, составляет 2,8•107 Па, так как реальные жидкости менее прочны. Обычно же разрыв возникает при давлениях, лишь немного меньших давления насыщенного пара. Низкая прочность реальных жидкостей связана с наличием в них, так называемых кавитационных зародышей: микроскопических газовых пузырьков, твердых частиц с трещинами, заполненными газом и другие. Мельчайшие пузырьки газа или пара, двигаясь с потоком и попадая в область давления p < pкр, сильно расширяются в результате того, что давление содержащегося в них пара и газа оказывается больше, чем суммарное действие поверхностного натяжения и давления в жидкости. В результате на участке потока с пониженным давлением создается довольно четко ограниченная «кавитационная зона», заполненная движущимися пузырьками, рис. 1.
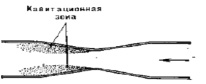
Рис. 1. Образование кавитационной зоны в сопле Лаваля
Для характеристики течения с кавитацией применяется безразмерный критерий α, называемый числом кавитации и равный [2]:
,
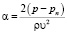где р – гидростатическое давление набегающего потока, рп – давление насыщенного пара, υ – скорость жидкости при достаточном удалении от тела, ρ – плотность жидкости.
Обычно число кавитации α определяют на входе в тот или иной агрегат, внутри которого возможно возникновение кавитации. Значение α, при котором в системе начинается кавитация, называется критическим числом кавитации.
Скорость потока воды из сопло Лаваля, при которой начинают наблюдаться кавитационные процессы на выходе сопла Лаваля былы в интервале υ = 20–30 м/с. Экспериментальные исследования процессы образования кавитационных пузырьков(КП) при прохождении водяной струи через сопло Лаваля проведены с соплом Лаваля с соответствующими диаметрами 15 мм (вход) и 1 мм (выход сопла) и длиной 35 мм. Для рассматриваемого сопла Лаваля порог наблюдения кавитации соответствовал числам Рейнольдса
Re = υ0d0/ν ≥ 2∙104,
где ν – вязкость воды при температуре 25 °С. При дальнейшем увеличении скорости водяной струи обеспечивается формирования устойчивых КП в виде кавитационной нити типа»ожерелья» из пузырьков, с разрывами между пузырьками.
Порог возникновения кавитации можно оценивать по параметру кавитационного числа на основании закона Бернулли α [2, 4]
α = р0/ρυ2 (1)
Здесь р0 – гидростатическое давление, υ – скорость потока жидкости. В нашем случае α = 25–26.
По параметрам скорости струи из сопла, выявлены пороговые параметры кавитационных процессов и образования устойчиво пульсирующих КП. В эксперименте кавитационные пузырьки образовывались как с добавками углеводородного топлива, так и в чистой воде. Существенного различия в динамике образования КП в чистой воде и с частицами топлива не обнаружено. Таким образом, разработан относительно простой метод генерации КП в воде с помощью сопла Лаваля при пропускании воды через сопла со скоростью более υ = 20 м/с и числом Рейнольдса Re ≥ 20000 с кавитационным числом α = 25–26.
Изучение коэффициента кавитации (число кавитации) при пропускании через сопло Лаваля можно описать с помощью понятий «вход» и «выход». Тогда процесс коэффициент кавитации пузырьков может быть успешно исследован на основе общей теории синергетики [3]. Процесс образования кавитационных пузырьков после прохождении воды через сопло Лаваля состоит из следующих двух процессов:
- подача воды – вход (подвод воды к сопло Лаваля);
- прохождение водяной струи через сопло Лаваля под действием гидродинамического давления – выход (выход воды через сопло и образование пузырьков).
Тогда эффективность коэффициента кавитации водяной струи при прохождении водяного потока через сопло Лаваля можно выразить в виде:
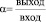. (2)
Пусть вход потоковой системы характеризуется потоком Ie и обобщенной силой Хе, а выход потоком Ii и обобщенной силой Xi. Общую связь между термодинамическими потоками и силами для необратимых процессов можно записать в виде уравнения Онзагера:
Ik = LkiХi, (3)
где Lki – феноменологические коэффициенты или коэффициенты Онзагера.
Здесь коэффициенты Lki характеризуют взаимосвязь процесса k с процессом i. В термодинамике неравновесных процессов для феноменологических коэффициентов выводится соотношение взаимности Онзагера, которое утверждает, что матрица коэффициентов {Lki} в выражении (3) является симметричной, т.е. перекрестные коэффициенты равны между собой: Lki = Lik.
Это означает, что имеется некоторая симметрия во взаимодействии различных процессов: возрастание потока Ik, обусловленное увеличением на единицу силы Xi, равно возрастанию потока Ii, обусловленному увеличением на единицу Xk.
На практике обычно используются не просто коэффициенты Lik, а некоторые пропорциональные им величины, так, например, коэффициент вязкости, теплопроводности и др.
Тогда эффективность коэффициента кавитации водяной струи при прохождении воды через сопло Лаваля примет вид:
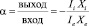, (4)
где Ie – гидродинамический поток воды на входе, Ii – гидродинамический поток кавитационных пузырьков на выходе сопло Лаваля, знак «–» в этом соотношении показывает существенное знаковое отличие входящих и выходящих потоков воды через сопло: Ii Xi > 0, и – Ie Xe > 0.
Применительно к процессам с неравномерным (нестационарным) прохождением воды через сопло Лаваля водяные потоки связаны между собой следующим образом:
Ii = Lii Xi + Lie Xe (5)
Ie = Lei Xi + Lee Xe (6)
Подставляя (5) и (6) в (4) получим для двухпотоковой системы:
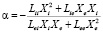. (7)
Умножим числитель и знаменатель в (7) на
.
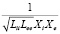Тогда выражение (7) примет вид:
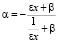, (8)
где 
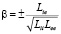и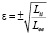 
– управляющие параметры; 
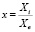– параметр порядка.
Значения εx и β лежат в пределах:
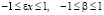, тогда 
.
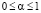График зависимости α = f(εx) имеет вид (рис. 2).
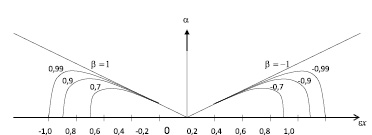
Рис. 2. График зависимости эффективности коэффициента кавитации водяной струи при прохождении воды через сопло Лаваля под действием гидродинамического потока воды от εx
Из рис. 2 видно, что эффективное значение коэффициента кавитации водяной струи, кроме β = ±1, принимает максимальное значение только для фиксированного значения εx.
Из условия экстремума функции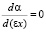 
следует, что максимальное значение αmax при заданном значении εx равно:
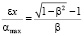. (9)
Библиографическая ссылка
Ысламидинов А.Ы., Абдалиев У.К., Ташполотов Ы. ОБРАЗОВАНИЕ КАВИТАЦИОННЫХ ПУЗЫРЬКОВ ПРИ ПРОХОЖДЕНИИ ВОДЯНОЙ СТРУИ ЧЕРЕЗ СОПЛО ЛАВАЛЯ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 7-5. – С. 776-778;URL: https://applied-research.ru/ru/article/view?id=9957 (дата обращения: 23.11.2024).